2. Принятие решений и элементы теории игр.

2.1. Задачи многокритериальной оптимизации.

Пусть xX, и f₁(x),…,f_n(x) различные критерии.

Пример. При проектировании самолета (x) возникают критерии: надежность f₁, скорость f₂, стоимость f₃, комфортабельность f₄, и т.п. Какой проект выбрать?

Принципы принятия решения:

Выбор главного критерия	Свертка критериев	Принцип Парето
	extr	все критерии желательно максимизировать
 ii0 (вводим ограничения на другие критерии)	Для оценки весовых коэффициентов i привлекают экспертов, но конкретную величину назвать невозможно	i fi(x)fi(y)   i0: fi0(x)fi0(y)  x y т.е. x лучше y (предпочтительнее).

№10. Построение свертки критериев. Пусть эксперт указал, что х "лучше" y,

причем z^xy={f_i(x)-f_i(y)} известные вектора, а в качестве вектора ={_i} возьмем точку выпуклой оболочки множества Z, ближайшую к началу координат. Если точка G (некоторой грани оболочки), то вектор (-0)G. Задача не имеет решения, если =0.

Пример. Есть 4 факультета, оцененные по двум показателям f₁ и f₂, и по мнению эксперта Х₁ Х₂, X₁ X₃, X₃ X₂. На какое место поместить Х₄?

Факультеты	Критерии		Свертка критериев F(X)=1 f1(X)+2 f2(X)	Место
	f1	f2
Х1 X2 X3 X4	25 30 10 45	25 20 30 15	F(X1)=3*25+7*25=250 F(X2)=3*30+7*20=230 F(X3)=3*10+7*30=240 F(X4)=3*45+7*15=240	1 4 2-3 2-3

Решение:

Построим свертку критериев ; X1 X2z12=(f1(Х1)f1(Х2), f2(Х1)f2(Х2))=(5,5), X1 X3z13=(f1(Х1)f1(Х3), f2(Х1)f2(Х3))=(15,5), X3 X2z32=(f1(Х3)f1(Х2), f2(Х3)f2(Х2))(20,10). Ближайшая к началу координат точка выпуклой оболочки множества Z лежит на отрезке [z32 z13].    (z32z13)=(35,15)  =(15,35) или (3,7) Значения свертки критериев см. в таблице.

Ответ: По свертке критериев факультет Х₄ делит 2-3 место.

Заметим, что ограничения - строгие линейные неравенства, а функционал – квадратичная функция, т.е. мы имеем задачу квадратичного программирования.

Л инейный алгоритм построения свертки в ².

Ближайшая к нулю точка может лежать на отрезке, и концы его в процессе поиска отбрасывать нельзя. Поэтому бинарный поиск аналогично алгоритму Меджидо ведем не по исходным объектам - точкам, а по парам объектов.

1. Найдем минимальный конус, содержащий исходные точки, т.е. опорные прямые l и r и точки L и R. Если угол  L0R > 180°, то 0  conv(L,1,R) и задача не имеет решения.

2. Удалим точки, лежащие над хордой LR, а остальные разобьем на пары. Замкнутый конус K[l,r] с направляющими l и r задает на каждой паре x:y одно из 4-х отношений: “x ВЫШЕ y“  “y НИЖЕ x“  x  y+K[l,r], “x ПРАВЕЕ y“  “y ЛЕВЕЕ x“  x  y+K(r,-l). В парах с отношениями ВЫШЕ и ПРАВЕЕ сменим ориентацию на НИЖЕ и ЛЕВЕЕ.

3. В парах с отношением НИЖЕ удалим более далекие от нуля точки. Для остальных пар найдем медиану m, опорную q, параллельную m, и множество Z крайних на q точек.

4. Основание P опущенного из 0 на q перпендикуляра дает решение, если P  conv (Z). Иначе перпендикуляр надо повернуть в сторону Z. При вращении в половине пар (слева или справа от m) одна из точек заведомо не будет крайней и мы ее отбросим.

5. Коррекция конуса: опорную l и точку L (если P справа от Z на q) или r и R (если P слева от Z) меняем на q и Z и повторяем шаги 2-5 с оставшимися точками, пока n > 2.

Вместо поиска точки на участке [L, R] границы выпуклой оболочки мы продолжим поиск на участке [L, Z’] или [Z’, R] с числом точек, уменьшенном на ¼ (ради чего и ищем медиану). При сокращении участка поиска угол между направляю­щими конуса l и r растет, стремясь к 180°. Трудоемкость алгоритма линейна, т.к. .

Пример. Результаты счета см. в таблице. На рисунках медиана отмечена красным цветом. Она выбирается по значению синуса угла между хордой LR и направлением пары, ориентированной вправо.

i	X	Y		S	0	0	Удаления	Пары		Sin	m	Z	P
1	0	3		l	1	-5	Шаг 2 (над хордой): 8	3	4	0	6  5	2	справа от Z
2	0	2		r	-4	1	Шаг 3: 1 (выше 2)	2	7	0,1688
3	-1	5		R-L	5	-6	Шаг 4: 3, 6	6	5	0,0501
4	4	-1
5	3	0		S	2⅔	-⅔
6	1	2		l	2	-2	Шаг 2: 7, 5	2	4	0	2  4	2, 4	P  conv(Z)
7	2	1		r	-4	1							0,96
8	2	3		R-L	4	-3							1,28

№11. 2.2. Принятие решений в условиях неопределенности.

Функция f зависит от неизвестного y, избавиться от которого можно так:

a) Принцип пессимиста . Пример – при строительстве моста.

b) Принцип оптимиста . Пример – снятие вратаря в хоккее.

c) Принцип прагматика:

–информированный прагматик  , M_yматематич. ожидание;

неинформированный прагматик  или .

Пример: Лыжные соревнования. Пусть {Xi} – виды лыжной мази, {Yi} –состояния погоды с известными информированному прагматику вероятностями: р1=0,3, р2=0,6, р3=0,1.

	погода			F(x) для каждого типа критерия
	Y1	Y2	Y3	Пессимист	Оптимист	Информ.прагматик	Неинформ.прагматик
X1	0,6	0,8	0,4	0,4	0,8	3*0,6+6*0,8+1*0,4 =7	0,6+0,8+0,4=1,8
X2	0,5	0,3	0,85	0,3	0,85	3*0,5+6*0,3+1*0,85=4,15	0,5+0,3+0,85=1,65
X3	0,6	0,7	0,5	0,5	0,7	3*0,6+6*0,7+1*0,5=6,5	0,6+0,7+0,5=1,8
X4	0,2	0,4	0,95	0,2	0,95	3*02+6*0,4+1*0,95=3,95	0,2+0,4+0,95=1,55

Так как чаще встречаются Х1 и Х3, то лучше использовать одну из этих мазей.

Вероятностный подход к ЗРО. Байесовский классификатор

Будем считать, что для любого класса есть функция плотности .

- вероятность класса , если мы попали в точку . . Разделяющей гиперплос­кости не может быть в принципе, т.к. любая точка может попасть в любой класс со своими вероятностями. Возможен только вероятностный подход. Рассмотрим байесовскую модель принятия решения.

П

усть матрица , где - штраф, который мы платим за отнесение элемента из класса к классу . Посчитаем математическое ожидание штрафа , - настоящий номер класса, - номер назначенного класса, . По формуле Байеса:

P(K_j) – априорные вероятности. не зависит от

 решающее правило Байеса: ,

Пусть есть 2 класса и .

Относим 

Будем считать, что для и . Тогда ,

.

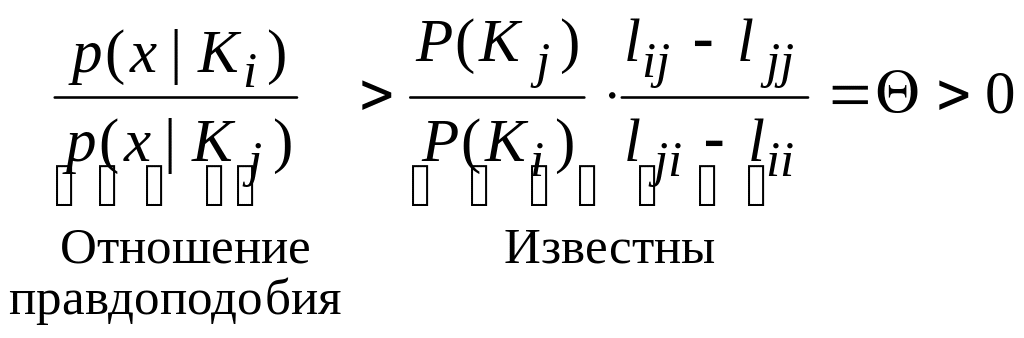
Байесовский классификатор:  . Частный случай: матрица L стандартная.

П

ри этом

Правило: .

Рассмотрим байесовский классификатор для случая нормального распределения.

, где

Если , то , где

- уравнение гиперплоскости.

М

Байесовский классификатор для двух нормально распределенных классов строит линейную (при ) или квадратичную ( при ) разделяющую поверхность.

етод безытерационный, поэтому часто сначала разумно построить байесовский классификатор.