1.4. Понятие о nр-полноте.

Алгоритм, решающий задачу Z, строит по входной информации выход­ную. Трудоемкость алгоритма будем оценивать как функцию от объема входа.

Пример: возведем 2 в степень n. Длина входа = log(n). Трудоемкость алгоритма равна n = 2^{log n}, т.е. зависит от объема входной информации экспоненциально.

Будем различать 3 типа задач поиска:

1. оптимизационный: найти вектор x ^оптD, такой что (x^опт) = extr (x).

2. вычислительный: найти число ^опт такое, что ^опт = extr (x).

3. распознавания: существует ли (да или нет =1 бит) xD такой, что (x) > L?

Все типы задач можно свести к варианту распознавания свойств.

НЕФОРМАЛЬНОЕ ОПРЕДЕЛЕНИЕ NP-ПОЛНОТЫ.

Говорят, что массовая задача распознавания Z принадлежит классу NP, если существуют такие полином P_z и алгоритм A_z, что для каждой индивидуаль­ной задачи (Z,I) с ответом “да” существует краткое удостоверение x ответа, быстро проверяемого алгоритмом A_z (т.е. и ). Краткого удостоверения ответа “нет” при этом может и не существовать.

Рассмотрим это определение на примере задачи коммивояжера (ЗК). Пусть на входе - матрица расстояний размера nn и M – максимальное число в ней. Вариант распознавания ЗК: есть ли гамильтонов путь, длина которого меньше L?. Для проверки ответа “нет” в полном графе пришлось бы проверить все n! гамильтоновых путей. Удостоверение ответа “да” – путь, длина которого < L. Общий объем входа |I| = n²·log M + log L бит и |x| = n·log n - для записи n чисел из диапазона от 1 до n. Алгоритм проверки удостоверения очевиден – подсчет длины пути и проверка его гамильтоновости: берем из матрицы нужные числа, складываем их и сравниваем сумму с числом L. Это требует n·log M операций для подсчета длины пути и log L операций для сравнения с L. В качестве полинома P_z возьмем P_z(t) = t.  Как и многие прикладные задачи, ЗК  NP. Это означает, что она выполнима за полиномиальное время на недетерминированной машине Тьюринга. Некоторые задачи (такие как МОД, ЛП) могут быть решены за полиномиальное время и на детерминированной машине. Самыми сложными в классе NP являются т.н. NP–полные задачи.

Говорят, что задача Z является NP–полной, если: 1) ZNP, 2) к ней полиномиально может быть сведена любая другая задача из класса NP.

Пусть есть две задачи Z₁ и Z₂ со входами V₁, V₂ и выходами W₁, W₂. Пусть известен алгоритм A₁ решения задачи Z₁, и по входу второй задачи мы умеем строить вход первой (A₂₁), а по выходу первой – выход второй (A₁₂). Тогда задачу Z₂ можно решать алгоритмом A₂=A₁₂*A₁*A₂₁, т.е. сводя ее к Z₁. Сведение полиномиально, если алгоритмы A₁₂ и A₂₁ имеют полиномиальную трудоемкость относительно длины входной информации.

Если хотя бы для одной NP–полной задачи будет найден полиномиальный алгоритм, то все задачи класса NP окажутся полиномиально разрешимыми. Но пока этого не смог сделать ни один математик в мире. Наивно предполагать, что это сделаете именно Вы. Доказательство NP–полноты массовой задачи Z дает Вам право приближенно решать индивидуальную задачу Z больших размеров.

Задача ВЫПОЛНИМОСТЬ.

Дана булева функция  F (x₁, , x_n) в виде К.Н.Ф.   .

Существует ли вектор x, выполняющий формулу F (т.е. F(x) = “истина”)?

Легко видеть, что ВЫПОЛНИМОСТЬ NP. Удостоверением ответа “да” является выполняющий формулу F набор истинности. Для проверки надо один раз пройти по всей формуле, и убедиться, что все сомножители равны 1. Т.е. P_z(t)=t. Кук показал полиномиальную сводимость любой задачи из NP к задаче ВЫПОЛНИМОСТЬ  ВЫПОЛНИМОСТЬ NP–полна. А как доказать NP–пол­ноту иной задачи? Достаточно проверить ее принадлежность классу NP и свести к ней какую-либо известную NP–полную задачу, например, ВЫПОЛНИМОСТЬ. В самом деле, если Z₁ NP–полна и полиномиально сводится к Z₂, то любая другая задача из NP сводится к Z₂ полиномиально, т.к. суперпозиция двух полиномов со степенями m и n является полиномом степени m  n.

NP–полнота целочисленной задачи ЛП (ЦЛП).

1) Покажем, что ВЫПОЛНИМОСТЬ полиномиально сводится к ЦЛП, построив алгоритм преобразования произвольного входа задачи ВЫПОЛНИМОСТЬ (т.е. любой КНФ) в систему линейных неравенств для ЦЛП: литерал без отрицания переходит в арифметическое выражение без изменений, а литерал с отрицанием – по правилу: . Например, булева формула эквивалентна системе арифметических неравенств x₁+ (1- x₂) + x₇ + (1 - x₁₉)  1, x_i  0, x_i  1. Тогда это есть вариант распознавания для задачи ЦЛП.

Оптимизационный вариант для ЛП:

Вариант распознавания для ЛП:  ли x : .

2) Проверим, что ЦЛП  NP. Здесь главный вопрос - краткость удостоверения x.

Пусть целочисленные параметры ограничены константой М: .

В качестве удостоверения x возьмем вершину многогранника ограничений, являющуюся оптимальным решением задачи ЛП и получим, верхнюю оценку координат вектора x. Пусть - уравнения, определяющие оптимальную вершину x, - невырожденная квадратная матрица и . Тогда , , где A_ij – минор матрицы A. Т.к. A – целочисленная, то знаменатель по модулю не меньше 1, а числитель – это сумма произведений, каждое слагаемое  M^n-1, а число слагаемых = т.е.   длина |x| удостоверения x не превосходит . Т.к. вход имеет длину  длина удостоверения меньше двух длин входа  удостоверение краткое. Значит, ЦЛП NP и NP-полна.

Кстати, обычная задача ЛП полиномиально разрешима. А условие целочисленности сильно усложняет задачу: - она теряет свойства выпуклости и непрерывности. И в худшем случае приходится перебирать все варианты.
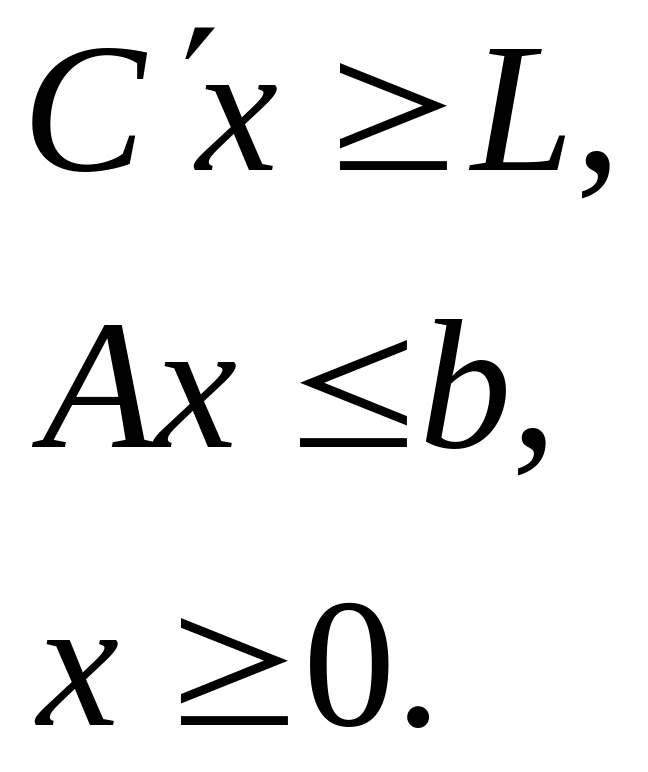