1.2. Оптимизационные задачи в 2.

Пример: Проектирование кабельной сети передачи данных. Надо стремиться:

1. Минимизировать расход кабеля.

2. Повышать связность сети = число независимых путей передачи информации.

3. Создавать систему технического обслуживания, если узлы связи ненадежны.

ЗадачаА. Пусть все пункты абсолютно надежны. Нужно соединить их связной сетью, минимизируя расход кабеля, и вводя, возможно, дополнительные точки.

Рассмотрим частные случаи задачи.

Построение минимального остовного дерева (МОД). Алгоритм Краскала.

Ребра в порядке возрастания длин добавляем в дерево, если не возникает цикл.

П усть NKS(i) – Номер Компоненты Связности, сначала NKS(i)=i. Добавим ребро (i,j). Цикл возникает  NKS(i) = NKS(j)  ребро отбрасываем. Иначе две компоненты сливаются в одну  у всех вершин менее мощной компоненты изменим номер. При этом каждая вершина изменит свой NKS не более log₂n раз  число всех коррекций NKS не превзойдет n·log₂n. Пусть MKS(k) – мощность k-й компоненты связности и MKS(1) > MKS(7)  при добавлении ребра R номер общей компоненты равен 1. Для перебора вершин по компонентам нужны: NNK(k)– начальный номер вершины в компоненте k и NSV(i) –номер следующей за i вершины в своей компоненте. Сортировка ребер (их O(n²)) определяет трудоемкость алгоритма - O(n²·log n).

Теорема. Если точки лежат в ² и расстояния – евклидовы, то в МОД войдут только ребра между соседними по Вороному вершинами. Таких ребер < 3n  в ² можно строить МОД алгоритмом Краскала за O(n·log n) операций.

В третьей части мы рассмотрим алгоритм Тарьяна-Черитона [1976] построения МОД с трудоемкостью O(n) для планарных графов и O(n²) в общем случае.

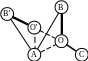
№ 3 Медиана 3-х точек (Зейдель). Разместить базу снабжения 3-х магазинов, имеющих товарообороты m1m2m3. Вершины помечены товарооборотами 5, 4, 3. Если m1m2+m3, то размещаем базу в точке m1. Иначе строим треугольник со сторонами, равными m1, m2 и m3. Обозначим углы, лежащие против сторон: m1 – , m2 –  и m3 - . Из 1-й точки отложим вне треугольника угол  от обеих сторон, из 2-ой – угол , и из 3-ей – угол . Соединив лежащие на пересечении углов точки A и B с противоле­жащими вершинами треугольника, получим в пересечении точку O, оптимальную для размещения базы. Ее при­тягивает к себе магазин с наибольшим товарооборотом.

Доказательство проведем для случая, когда m_i =1 i  углы  =  =  = 60. Повернем треугольник ABO на 60 в противоположную от точки C сторону. Т.к. треугольник AOO правильный, а треугольники AOB и AOB равны, то . Сумма отрезков AO, BO и CO равна длине ломаной B′O′OC. Минимум суммы достига­ется, когда ломаная станет прямой. Не зная положения точки O, построим точку B′ поворотом стороны AB на 60 и соединим B′ отрезком с точкой C. Аналогично, повернув АС на 60, соединим отрезком точки C и B. Точка O лежит на пересечении отрезков BC и CB. Рассуждения верны, когда все углы треугольника < 120. В противном случае в качестве точки O надо брать вершину тупого угла.

№4. Задача Штейнера. Связать n точек на плоскости минимальной сетью с дополнительными точками (без учета интенсивностей источников нагрузки в точках). Сеть определяется положением D-точек и структурой, т.е. списком ребер. Если положение D-точек известно, то сеть - это легко находимое МОД.

Пусть известна структура сети. Если в дереве оставить только D-точки и инцидентные им ребра, то дерево разобьется на ком­поненты связности, причем D-точки связаны между собой, если они лежат в одной компоненте. Вернув в каждую компоненту инцидентные ее вершинам ребра и их концы – основные точки, мы получим компоненты Штейнера (КШ). Невисячие вершины КШ –D-точки  все внутренние углы КШ = 120. Число D-точек в компоненте с k вершинами = k-2, число ребер =k+(k-2)-1=2k-3.

При замене пары соседних по структуре точек А и В на В´ число основных и дополнительных вершин уменьшается на 1, а длина сети остается неизменной (сумма трех отрезков АО, ВО и СО равна длине отрезка В´С). Уменьшив число вершин до двух, получим отрезок с базовым направ­лением  и длиной = длине сети с заданной структурой (исп. при сравнении вариантов структур)

Направления  + _k  отрезков сети имеют 3 типа, т.е. _k {0, +60, -60}. После нахождения направлений повторяем вычисления, заменяя построение _∆ABВ ́ на _∆ABO Для этого из вершин А и В проводим лучи с направлениями  + _k  находим вершину О (на рис. ставим номер на _∆-к).

При проходке 1 определяем смещения _k , затем базу , а при проходке 2 – сами D-точки.

П ример. k =5, r =2 5 -3 =7

Нерекурсивный алгоритм нахождения координат D-точек при заданной структуре за O(n).

0) Выделить компоненты Штейнера и для каждой компоненты выполнить:

1 ) Расставить пометки типов направлений на ребрах КШ (3типа).

2) Построить последовательность треугольников наружу с углами 60°.

3) Получить базовый отрезок с базовым направлением и длиной сети.

4) Построить последовательность треугольников внутрь с известными углами.

З аметим, что искать надо не только координаты D-точек, но и структуру сети. Число различных структур конечно, но с ростом n растет по экспоненте  для поиска структуры применяют эвристические алгоритмы. Мы будем строить МОД и для вершин углов, мень­ших 120°, решать задачу Зейделя.

S²= (³/₂)² + (^√3/₂)² = 3

Алгоритм с выбором структуры: а) Находим и удаляем наиболее далекую в Х вершину х (удаление которой максимально уменьшает диаметр Х).

б) Рекурсивно строим дерево Штейнера на n-1 вершинах (м.б. неоднозначно).

в) Цепляем точку х к дереву через одного из ее соседей по Вороному.

г) Если угол < 120°, то внутри угла ставим дополнительную точку и соединяем ее с тремя вершинами угла, а старые стороны угла удаляем.

Рекурсивный алгоритм нахождения координат D-точек по заданной структуре сети.

Пусть V – множество вершин, n – их количество.

1. Если n  3 – решение тривиально.

2. Выбираем пару соседних по структуре точек a и b.

3. Строим правильный треугольник на стороне ab и обозначаем вершину c.

4. Решаем рекурсивно задачу на множестве точек .

5. Решаем задачу для треугольника (a,b,d), где d – точка, связанная с точкой c в структуре, полученной на шаге 4.

П ример. Заменив точки 1 и 2 на точку 12, а точки 4 и 5 на точку 45, решаем последовательно задачи: B=Z₃(12,3,45), A=Z₃(1,2,B) и C=Z₃(B,4,5). Процесс построения запишем условно с помощью операций + (строим правильный тре­угольник), – (проводим отрезок), пересекаем прямые:

1) 1 + 2 = 12 5) 12 – 345 = La 9) 1 + B = 1B 13) B + 4 = B4

2) 4 + 5 = 45 6) 123 – 45 = Lc 10) 2 – 1B = L2 14) B4 – 5 = L5

3) 12 + 3 =123 7) La  Lc = B 11) La  L2 = A 15) Lc  L5 = C

4) 3 + 45 = 345 8) 3 – B = L3 12) A – 1 = L1 16) C – 4 = L4

№ 5. ДИАГРАММА ВОРОНОГО И ГРАФ ДЕЛОНЕ.

Пусть есть n магазинов x_j, заданных своими координатами. Выделим для каждого из них зону обслуживания, предполагая, что покупате­ли ходят в ближайший магазин. Тогда зоны обслуживания суть множества , называ­емые клетками Дирихле или многоугольниками Вороного. Совокупность всех таких многоугольников называется диаграммой Вороного. Магазины назовем соседними, если их многоугольники имеют общий участок границы. У нас соседями будут пары: (1,2), (1,4), (2,3), (2,4), (3,4). Соединив все пары соседних вершин ребрами, получим граф Делоне. Он задает наилучшую триангуляцию карты (минимальный угол в триангуляции Делоне - наибольший по всем триангуляциям). Число ребер в диаграмме и в графе Делоне считается по формуле 3·(n-1)-G, где G – число точек, лежащих на границе выпуклой оболочки. Диаграмма строится рекурсивно методом “разделяй и властвуй” за O(n·log n) операций (т.к. ):

1. Найдем медиану среди первых координат точек и разобьем точки на два равных подмножества L и R, выпуклые оболочки conv(L) и conv(R) которых не пересекаются.

2. Построим диаграммы Вороного ДВ(L) и ДВ(R) для каждого из подмножеств.

3. По ДВ(L) и ДВ(R) за линейное время построим conv(L) и conv(R), и выполнив шаг 3 алгоритма Грэхема (см. ниже) – границу conv(X). На ней найдем два опорных отрезка (верхний и нижний), концы которых лежат в разных множествах L и R.

4. П остроим ломаную B, каждая точка z которой равноудалена от ближайших к z в множествах L и R точек l=l(z) и r=r(z). Двигаясь вверх по срединному перпендикуляру к текущему отрезку (начиная с нижнего опорного) до первой точки пересечения с отрез­ком одной из диаграмм, мы попадем в зону близости другой точки этой диаграммы  меняем l или r. Дойдя до верхнего опорного отрезка, завершим построение ломаной B.

5. Склеим две диаграммы в одну, удалив все части диаграммы ДВ(L), расположен­ные справа от ломаной B, и все части диаграммы ДВ(R), расположенные слева от B.

Пример: L = {1,2,4}, R = {3,5,6}.

Опорные отрезки – (1,6) и (2,5).

текущие	l	1	4	4	2	2
отрезки	r	6	6	3	3	5

Диаграмма Вороного полезна при решении многих оптимизационных задач на плоскости и ее построение выносится в предобработку. Она задает топологию на конечных множествах в ².

№6. ПОСТРОЕНИЕ ВЫПУКЛОЙ ОБОЛОЧКИ В ².

Алгоритм Грехема. На входе - множество X={x_i}, состоящее из n точек плоскости.

1. Выберем внутреннюю точку O (например, центр тяжести любых 3-х точек).

2. Упорядочим полярные углы из O на точки x_i и перенумеруем точки.

3. В цикле для тройки (l,k,r) проверим, лежит ли точка k внутри conv(O,l,r), где l=L(k), r=R(k), т.е. l и r - соседи слева и справа от k по оставшимся углам. Если лежит, то удаляем k {L(r)=l, R(l)=r} и делаем шаг назад {k=r, r=R(r)}, проверяя r conv(O,l,R(r)). Если же нет, то идем вперед: {r=k, k=l, l=L(l)}. Цикл идет до тех пор, пока некоторая тройка не повторится.

С уммарное число шагов вперед < 2n, шагов назад < n. А общая трудоемкость алгоритма определяется на шаге 2 и равна O(n·log n).

Пример: Выберем точку О как центр тяжести любых трех точек исходного множества точек. Упорядочим точки по полярному углу из точки О. Выполним шаг 3 алгоритма:

тройка (2,1,6) - 1 лежит справа от отрезка [2,6]  2 не принадлежит выпуклой оболочке  идем вперед. Результат занесем в таблицу (цикл по средней точке от 1 до n и замыкаем на 1 до повтора тройки ???):

тройка	2,1,6	3,2,1	3,1,6	4,3,1	5,4,3	6,5,4	1,6,5	1,5,4	3,1,5	3,5,4	4,3,5	5,4,3
команда	вперед	назад	вперед	вперед	вперед	вперед	назад	вперед	назад	вперед	вперед

Алгоритм «Разделяй и властвуй».

Разделим точки пополам произвольным образом. Для двух множеств решим задачу рекурсивно, и соединим построенные оболочки. Как соединять? Берем внутреннюю точку (центр тяжести) одной оболочки. Построим полярные углы из нее на точки обоих оболочек. Если выбранная точка лежит вне выпуклой оболочки второго множества, граница второго множества разбивается на два участка, на одном из которых углы при обходе границы против часовой стрелки убывают, а на втором - возрастают. Удалим внутренние точки участка убывания. Теперь все углы в обоих оболочках возрастают. Сольем их в одно упорядоченное множество углов и выполним шаг 3 алгоритма Грехема за линейное время. Из уравнения следует трудоемкость O(n·log n).

НАХОЖДЕНИЕ ДИАМЕТРА КОНЕЧНОГО МНОЖЕСТВА ТОЧЕК

Д ве точки a и b назовем противоположными в Х, если существуют две параллельные опорные (охватывающие все множество Х) прямые, проходящие через a и b.

противополож­ные точки	a	1	2	2	2	3	3	4
	b	4	4	5	6	6	1	1

Вращая опорные прямые вокруг выпуклой оболочки множества Х и сравнивая углы между ними и границей оболочки, получим все n пар противоположных точек, перебрав которые найдем наиболее удаленную пару – диаметр множества. В примере это пара (1,4).

Минимальная описанная окруж­ность опирается или на диаметр или на 3 точки и ее центр – вершина ДВ дальней точки (строится аналогично обычной ДВ).

ПОСТРОЕНИЕ ОГИБАЮЩЕЙ СЕМЕЙСТВА ПРЯМЫХ.

Дано n прямых. Требуется построить верхнюю/нижнюю огибающую. Используя метод “разделяй и властвуй”, делим все прямые на два множества, строим огибающие для каждого из них и сливаем их в общую огибающую. Алгоритм напоминает построение выпуклой оболочки, только точка наблюдения находится на бесконечности. Трудоемкость – O(n·log n).

1.3. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ (ЛП) В ⁿ.

Дадим экономическую интерпретацию параметров прямой задачи ЛП.

Планирование по валу. Пусть A = {a_ij 0} - технологическая матрица, где a_ij - расход i-го ресурса для производства единицы j-го товара,

x = (x₁,…,x_n)  0 - план выпуска товара, где x_j - количество единиц j-го товара, b = (b₁,…,b_m)  0 - вектор имеющихся ресурсов, c = (c₁,…,c_n) - вектор цен на товары. Тогда Ax – расход ресурсов (который не может быть больше b) , а c’x – подлежащая максимизации прибыль от продажи товара x. ‘ = знак транспонирования.

Планирование по номенклатуре. Если мы хотим, чтобы произведенного товара хватило на  комплектов (вектор показывает, сколько единиц каждого из товаров входит в 1 комплект), то , и требуется максимизировать .

задачи планирования по валу		по номенклатуре
прямая П	двойственная Д

Свойства прямой и двойственной задач.

Th1: Если x, y – допустимы в задачах П и Д (т.е. выполнены все неравенства-ограничения), то yb  cx.

Доказательство: yb  y (Ax) = (y A)x  cx.

Следствие: Если x, y допустимы и yb = cx, то x, y – оптимальны.

Th2: Если задача П допустима (т.е. существует допустимый x), а задача Д - недопустима, то задача П - неограничена.

Th3: Если задачи П и Д допустимы, то обе имеют решения, и yb = cx.

Th4 (о дополняющей нежесткости, ТДН). Предварительные обсуждения.

Пусть задачи П и Д допустимы, и (x, y) – оптимальные решения  (b–Ax)0, (c’–y’A)0, x0, y0, и по Th3 верно равенство yb = cx. Вычитая y’Ax из обеих частей равенства, получим c x- yAx = yb - yAx, или 0y’(b–Ax)=(c’-y’A)x0. Т.е. имеем y’(b – Ax)= 0 и (c’-y’A) x = 0, но в силу знакопостоянства компонент всех векторов получаем покомпонентные равенства y_j’(b–Ax)_j=0 и (c’-y’A)_ix_i=0

Формулировка ТДН.: Если задачи П и Д допустимы, то

(x, y) оптимальны  y_j’(b–Ax)_j=0 и (c’-y’A)_ix_i=0 для всех индексов i,j.

_{ЭКОНОМИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ПАРАМЕТРА y.}

П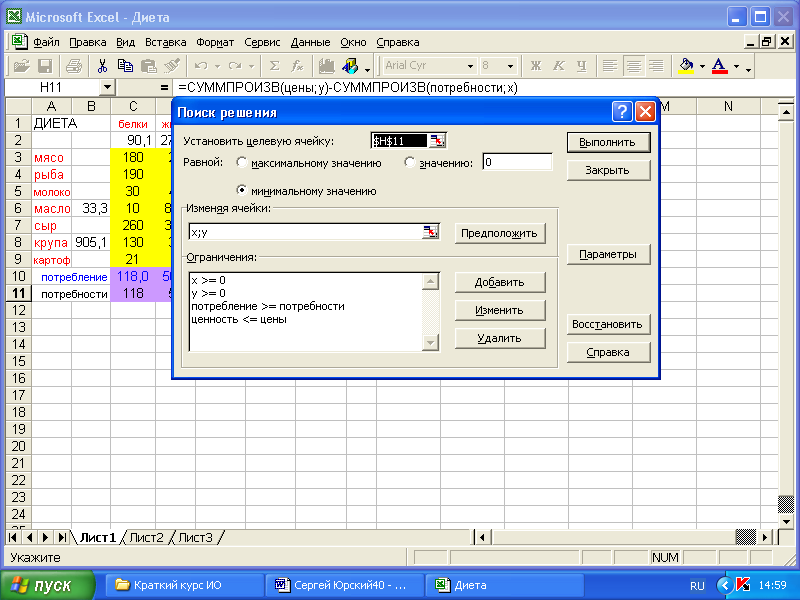 о ТДН, если (b - Ax)_i > 0, т.е. i-й ресурс имеется в избытке, то y_j =0, а если , то (b - Ax)_i = 0, т.е. весь ресурс выработан и его можно докупить. Прибыль равна c x = y b =  y_i b_i. y_i = и при изменении i-го ресурса на _i прибыль изменится на величину y_i_i Т.е. y_i является предельным значением цены ресурса, при которой производитель не терпит убытка. Ценность ресурса для производителя определяется производимыми товарами и выражает максимальную прибыль, какую может дать правильное использование единицы ресурса.

Приведем пример решения в EXCEL прямой и двойственной задач о диете.

№7. Пример: Проверить, является ли y*= (0, 1, 5/3) решением двойственной задачи

6y₁+4y₂+7y₃  min Выпишем ограничения прямой задачи и проверим их для y*:

y₁ +3y₃  5 5=5 x₁+3x₂ -x₃ 6

3y₁+y₂+ y₃  2 2⅔>2  x₂=0 x₂+x₃ 4 y₂0  x₂+x₃=4

-y₁+y₂  1 1=1 3x₁+x₂  7 y₃0  3x₁+x₂ =7.

y_j0 j=1,2,3 x_i0 i=1,2,3

Мы использовали условия ТДН: (c’-y’A)₂ ·x₂=0, y₂ ·(b-Ax)₂=0 и y₃ ·(b-Ax)₃=0.

Для решения прямой задачи имеем 3 уравнения с 3 неизвестными. x*=(⁷/₃,, 0, 4). Проверим ограничение 1 прямой задачи: ⁷/₃+3·0 –4<6  y* и x* - решения!

УСТОЙЧИВОСТЬ РЕШЕНИЯ В ЛП.

Пусть x, y - решение задачи ЛП с параметрами A,b,c. Предположим, что какие-нибудь параметры изменились. Останется ли пара (x, y) оптимальной?

1) Замена ресурса: bb+. Допустимость y остается, т.к. не зависит от b.

y A  c, y 0 Ax  b, x 0 Ax  b+    Ax–b - условия допустимости

(c -yA)_ix_i=0 y_j ·(b–Ax)_j=0 y_j ·(b+–Ax)_j=0  y_j ·_j=0 - оптимальности.

Из оптимальности пары (x, y) следует:

y_j>0  остаток ресурса (b–Ax)_j=0, т.е. ресурс дефицитный и _j=0

y_j=0  (b–Ax)_j0, т.е. ресурс достаточный и _j  (Ax–b)_j

Избыточный ресурс остается достаточным, а дефицитный – неизменным!!!

2) Меняем цену: cc+. Допустимость x остается, т.к. не зависит от с.

Новые ограничения: y A  c+    y A - c, (c + -yA)_ix_i=0  _i ·x_i=0

Из оптимальности пары (x, y) в обеих задачах следует:

x_i>0  товар производимый и _i=0, т.е. цена на него неизменна.

x_i=0  (c–yA)_i 0, т.е. цена не превышает ценности и _i  (yA– c)_i

Цены на производимые товары – неизменны, а на непроизводимые - неприбыльны.

Пример (продолжение): x* = ( ⁷/₃ , 0, 4 ) y* = (0, 1, ⁵/₃) , ε  Ax*-b

y₁ =0  ε₁  (Ax*-b)₁ = ⁷/₃ *1 +3*0-4-6=-7²/₃ , y₂, y₃ >0  ε₂= ε₃=0

Продавать можно остатки 1-го ресурса, а докупать в первую очередь 3-й.

x₁ , x₃ >0  δ₁ ,δ₃=0  локальное изменение цен на продукты 1 и 3 меняет прибыль, а на второй – нет.

δ₂  (y*’A-c’)₂ = 3*0+1+⁵/₃-2=²/₃ т.е. δ₂ ²/₃ , т.е. цена на товар 2 может увеличиться, но не более, чем на ²/₃.

ТРУДОЕМКОСТЬ ЛП.

Если в множестве {xAx b} есть хотя бы одна вершина, то решение ЛП можно искать среди его вершин. Вершинам n-мерного пространства соот­ветствуют системы из n равенств среди m ограничений. Число способов выбора = . Решение системы из n линейных уравнений имеет трудоемкость O(n³), вычисление функционала – O(n)  полный перебор - O( ).

Задача ЛП была впервые сформулирована в 1939 году Л.Канторовичем как инструмент планирования централизованной экономики СССР. В 1975 г. Канторович получил Нобелевскую премию по экономике. Д.Данциг (США, 1947) предложил для решения ЛП симплекс-метод, имеющий в худшем случае экспоненциальную трудоемкость. Математики всего мира долго пытались построить для ЛП полиномиальный алгоритм. Доказать полиномиальную разрешимость ЛП удалось Л.Хачияну (Москва,1979), используя обобщение на ⁿ метода половинного деления в ¹- метод эллипсоидов (Н.Шор, Москва, 1977).

Основная идея метода:

П ересечение конечного числа гиперплоскостей в ⁿ есть выпуклое множество M ⁿ. Экстремум линейной функции на M достигается на его границе G_M. Разложим ⁿ в прямую сумму линейной оболочки L, натянутой на вектор c, задающий линейный функционал, и ортогонального L под­пространства ^n-1. Границу G_M можно рассматривать как объединение графиков двух функций – выпуклой f_- и вогнутой f₊  f_-, заданных на M  проекции M на ^n-1. Заключим M в любой эллипс E и проведем в его центре a вычисления: найдем значения f и f = субградиент = направляющий вектор опорной к графику гиперплоскости. Из условия выпуклости f(x)  f(a) + f(a)∙ (x-a) следу­ет, что минимум надо искать в полупространстве f(a)∙ (x-a) < 0, т.к. f(x) > f(a). Оставшуюся половину эллипса заключим в новый эллипс E₁ и повторим вычисления в его центре и т.д. Юдин и Немировский (Москва,1976) показали, что отношение объемов V(E_k) / V(E_k-1) < ²⁽ⁿ⁺¹⁾√¯e ^-1 <1.  V(E_k)  0 в ^n-1. С ростом размерности пространства стремление к 0 замедляется, но место имеет. Хуже, что линейные расстояния при этом совсем необязательно стремятся к 0 (эффект оврага).

Однако вскоре было доказано, что полиномиальную трудоемкость имеет и алгоритм А.Левина (Воронеж,1965), названный методом центров тяжести. Б.Митягин (Воронеж,1969) доказал, что при рассечении любого выпуклого тела любой размерности любой гиперплоскостью, проходящей через его центр тяжести, объем любой его части составляет от е^-1  до 1-е^-1 объема тела.

С 1971 по 2004 год А.Ю.Левин работал в ЯрГУ, заведовал основанной им кафедрой теоретической кибернетики, из которой впоследствии вырос факультет ИВТ. На матфаке ЯрГУ ее преемницей является кафедра КБиММОИ.

Приводимый ниже алгоритм основан на близкой идее – уточняя на очередном шаге решение задачи мы уменьшаем объем не только локализатора (длину интервала), но и всей входной информации (часть ограничений отбрасываем).

№8. ЛИНЕЙНЫЙ АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ ЛП В ² (Megiddo,1983).

Пусть b>0. Введя обозначения X=x, Y=ax+by, получим более простую задачу:

Разобьем множество ограничений на 4 части: I⁺ ={i | _i>0 }, I^-={i | _i<0 }, I⁰⁺={i | _i=0 и _i>0}, I^0-={i | _i=0 и _i<0} и построим интервал [u₁, u₂], где u₂=+ при I⁰⁺=, иначе , и u₁=- при I^0-=, иначе . Если u₁>u₂, то исходная задача ЛП недопустима. Пусть . Построив нижнюю огибающую семейства прямых I⁺ и верхнюю огибающую семейства I^-, мы свели исходную задачу к виду:

F₊(x)max при ограничениях x[u₁, u₂] и F₊ (x)  F_- (x).

Алгоритм Меджиддо для задачи ЛП в ² имеет линейную трудоемкость, т.к. рекуррентное неравенство для трудоемкости имеет вид .

1. Элементы множеств I⁺, I^- разбиваем на пары и для каждой пары прямых ищем точку пересечения z_k. Если она (u₁, u₂), то удаляем одну из прямых: лежащую выше (т.е. y(z_k) больше), если (пара из I⁺ и z_k.u₁ ) или (пара из I^- и z_ku₂).

2. В множестве Z оставшихся точек пересечения ищем медиану m по координате x.

3. В точке m проводим вычисления (чтобы определить направление поиска):

   1. Сначала допустимость! = F₊(m)-F_-(m) вогнута и д.б. 0, иначе анализ производной 

   2. Определяем множество I^+m прямых из I⁺, на которых в m достигается min. Ищем в этой точке левую и правую производную функции F₊(x). . .

   3. Если обе производные > 0, то max следует искать справа (т.е. u₁=m). Если обе производные < 0, то max следует искать слева (т.е. u₂=m).

   4. Если переход с + на -, то m есть точка max. В противном случае надо смотреть на знак производной от разности F₊(m)-F_-(m).

4. Повторяем вычисления с пункта 1 на новом интервале, причем половина точек z_k окажется вне интервала, и для них отбрасываем одно ограничение из пары. В результате не менее четверти ограничений будет отброшено!

y  max	Пример:	Решение:
-x +y - 30 x +y-110 2x – y -70 -2x-3y +60 - x+2y - 70 4x + y-270 -x 0 -y 0	y  y1 = x + 3 y  y2 = 11 - x y  y3 = 2x -7 y  y4 = 2-⅔x y  y5 = ½(x+7) y  y6 = 27-4x x  x7 = 0 y  y8 = 0	I+={1,2,5,6} I-={3,4,8}	F+(x)=min{x+3; -x+11; ½(x+7); -4x+27} F-(x) = max{2x-7; - 2/3x+2; 0 }
		I0-={7} I0+=	u1=max{0/(-1)} =0 u2=+∞	U=[u1,u2]=[0,+∞)
		Точки пересечения пар прямых (i, j) из I+ и I-:
		(1,2): x + 3 = 11 – x  2x= 8  x=4 U (5,6): ½(x+7)=27-4x  9x=47  x=52/9 U (3,4): 2x - 7 = 2 - 2/3x  8x=27  x=33/8 U			X={4,52/9,3⅜} медиана(X)=4

F_-(4) =max{1; <0; 0}=1 < 5½ =min{7; 7; 5½; 11}= F₊(4)  m₁=4 допустима. Минимум был один  F₊(x) в окрестности точки m₁ совпадает с прямой y₅ = ½(x+7) и возрастает (y₅>0)  максимум находится справа от m₁  корректируем интервал: U=[m₁=4, +∞).

Анализируем пары прямых, точки пересечения которых оказались слева от интервала. Пара 1,2I⁺  можно отбросить прямую y₁, лежащую выше, т.к. y₁ =1 > -1= y₂; пара 3,4I^-  можно отбросить прямую y₄, лежащую ниже, т.к. y₄ = -2/3 < 2= y₃.

I^-={3, 8}. Ищем точку пересечения новой пары: 2x-7 = 0  x=3½ лежит слева от U  сразу отбрасываем прямую y₈ , лежащую ниже, т.к. y₈ = 0 < 2= y₃. Теперь I^-={3}.

I⁺={2,5,6}. Здесь оставляем пару (5,6), для которой x=5²/₉ є U. Она же медиана m₂. F_-(5²/₉) =2*5²/₉-7=3⁴/₉ < 5⁷/₉ =min{5⁷/₉; 6¹/₉; 6¹/₉}= F₊(5²/₉)  x=5²/₉ допустима. Минимум был один  F₊ в окрестности точки m₂ совпадает с y₂=11-x; y₂ =-1<0  F₊ убывает  ее максимум находится слева от m₂  переходим к интервалу: U=[4, m₂ =5²/₉]. Пара 5,6I⁺  отбрасываем прямую y₆, лежащую выше, т.к. y₅ =½ > -4= y₆.

I⁺={2,5}. Ищем точку пересечения новой пары: 11-x = ½(x+7)  x=5 U=[4, 5²/₉].

Других пар нет  m₃ =5. F₊(5)= min{y₂=11-5=6;y₅=½(5+7)=6}>3=F_-(5)  m₃ допустима.

Т.к. F₊(5) есть минимум пересекающихся прямых y₂ и y₅, то F₊^лев =max{y₂=-1; y₅=½}>0, F₊^прав =min{y₂=-1; y₅=½}<0. Производная меняет знак с + на -  m₃ - точка максимума.