Нахождение кратчайшего пути для ациклического орграфа

У тверждение 1: В ациклическом графе существует вершина, в которую не входит ни одна дуга.

Доказательство. Предположим противное. Возьмем любую вершину. По предположению в нее входит дуга. Перейдем в начало дуги, пометив его и т.д. Число вершин конечно  когда-то мы попадем в помеченную вершину и найдем цикл.

В ершины, в которые не входит ни одна дуга, поместим на слой 1 и удалим выхо­дящие из них дуги. В оставшемся графе снова возьмем вершины, в которые не входят дуги, поместим их на слой 2 и восстановим входя­щие в них дуги с предыдущих слоев и т.д.

Обработаем этот граф: D(1)=0 D(2)=d₁₂+D(1)=3, D(4)=d₂₄+D(2)=-1+3=+2,

D(5)=d₂₅+D(2)=-5+3=-2, D(3)= min{d₄₃+D(4), d₁₃+D(1)}=-4, D(6)= min{D(4)+4, D(3)+9, D(5)+2}=0. Кратчайший путь легко строится по вектору отцов.

Алгоритм работает для любого ациклического графа. Оценим его трудоемкость:

1. построение слоистой сети ~ числу дуг этого графа

2.  трудоемкость алгоритма ~ числу дуг, каждая дуга будет обработана 1 раз

В слоистой сети и в начальном графе число дуг совпадает.

№22. Задача сетевого планирования.

k	P.	tk	i	j	ij = wj – tij – i
1	-	10	S	1	w1 – 10 – S = 0
2	-	8	S	2	w2 – 8 – S = 14
3	1	12	1	3	w3 – 12 – 1 = 0
4	1,2	7	4	5	w5 – 7 – 4 = 19
5	2,3	14	3	5	w5 – 14 – 3 = 0
6	1,4,5	6	5	T	wT – 19 – 5 = 0
7	3,6	13

Дано множество работ {r_k} с длительностями t_k и отношение предшествования P между работами. Найти минимальное время, за которое можно выполнить все работы.

Работы будем обозначать сплошными дугами, а отношения предшествования (фиктивные дуги) – прерывистыми. Составим из работ слоистую сеть. На слой 1 поместим работы, которым ничего не предшествует. Работам следующих слоев предшествуют работы слоев с меньшими номерами, причем хотя бы одна работа с непосредственно предшествующего слоя.

Правила редукции графа. 1. Если концы фиктивной дуги связывает путь, то дугу можно удалить (из r₁ в r₆ и из r₃ в r₇).

2. Если в вершину втекает, или из нее вытекает единственная дуга, и она фик­тивна, то начало и конец дуги можно склеить (r₃ поглощает 2 дуги, r₅ и r₆ по 1).

3 . Две работы, следующих одна за другой, объединим в одну с суммарной дли­тельностью, если степень вершины на стыке равна 2 ( в примере - r₆ и r₇).

Объединим все вершины слоя 1 в вершину s, последнего слоя – в вершину t.

Пусть _i – самый ранний срок начала работ, выходящих из вершины i, а _i – самый поздний срок окончания работ, входящих в вершину i при условии, что весь комплекс работ будет завершен в минимальное время. Тогда

₁ = 0, _i = max _j{_j +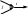  t_ji } _t = _t , _i = min _j{_j -  t_ij }

i	0	10	8	22	10	36	55
i	S	1	2	3	4	5	T
i	0	10	22	22	29	36	55

_ij = _j - t_ij - _i  - максимальная задержка работы, выполняющейся на отрезке (i,j).

Работу назовем критической, если _ij = 0. Путь критический, если все дуги в нем критические. Он – самый длинный в сети.

Двойственность в сетевом планировании.

Задача нахождения α_i= max{α_i+ d_ij} ~ задаче α_t- α_s→ min при α_i– α_j≥ d_ij

Она двойственна прямой задаче c’x → max, Ax = b, x ≥ 0 с параметрами: A - мат­рица инциденций, c ={d_ij} – длительности работ (реальных и фиктивных), x – единичный поток. Ограничения прямой задачи = уравнения баланса для потока. Матрица инциденций вполне унимодулярна  ЛП = ЦЛП  c’x = длина пути. Цель – найти максимальный путь. Граф ацикличен  задача полиномиальна.

Выделение критических работ и путей непосредственно следует из ТДН ???

Обратим внимание на то, что y=α в двойственной задаче y’b → min, y’A ≥ c’ может быть любым  ограничения прямой задачи имеют форму равенств. b=(-1,0 0,1).

Связь с NP ‑полной задачей МНОГОПРОЦЕССОРНОЕ РАСПИСАНИЕ.