4.2. Упрощение уравнения линии второго порядка

Определение 9. Линией второго порядка называется множество точек плоскости, которое в некоторой АСК можно задать уравнением второй степени от двух переменных.

Будем рассматривать линии второго порядка только в прямоугольной системе координат. При изучении этих линий прежде всего встают вопросы:

• Как выбрать такую систему координат, в которой линия имела бы наиболее простое уравнение.

• Какие существуют типы линий второго порядка.

Общий вид уравнения линии Г второго порядка:

Г: а₁₁х² +2а₁₂ху + а₂₂у² + 2а₁₃х + 2а₂₃у + а₃₃ = 0 (9)

Если в уравнении (9) коэффициент а₁₂ = 0, то уравнение (9) упрощается выделением полных квадратов (мы это сделаем ниже). Пусть а₁₂  0. Поставим вопрос, можно ли найти систему прямоугольных координат так, чтобы в уравнении линии Г не было слагаемого с произведением координат. Решить этот вопрос попробуем с помощью поворота прямоугольной системы координат. В этом случае формулы преобразования координат:

Подставив в уравнение (9), получим

а₁₁(х¹соs - у¹sin)² + 2а₁₂(х¹соs - у¹sin)(х¹ sin + у¹ соs) + а₂₂(х¹ sin + у¹ соs)² + + 2а₁₃(х¹соs - у¹sin) + 2а₂₃(х¹ sin + у¹ соs) + а₃₃ = 0.

Раскроем скобки, приведём подобные и запишем уравнение в виде

+ 2 (10)

Новые коэффициенты выражаются через старые по формулам:

(11)

В уравнении (10) не будет слагаемого с произведением координат тогда и только тогда, когда = 0, т.е. . Отсюда (12)

Итак, если систему координат повернуть на угол , определяемый по формуле (12), то в новой системе координат в уравнении линии Г не будет слагаемого с произведением координат. В этой системе координат уравнение будет иметь вид:

а₁₁х² + а₂₂у² + 2а₁₃х + 2а₂₃у + а₃₃ = 0 (13)

Возможны следующие случаи.

I. а₁₁  0, а₂₂  0. Выделим в правой части уравнения (13) полные квадраты.

а₁₁(х² + 2 х + ) + а₂₂(у² + 2 ) = .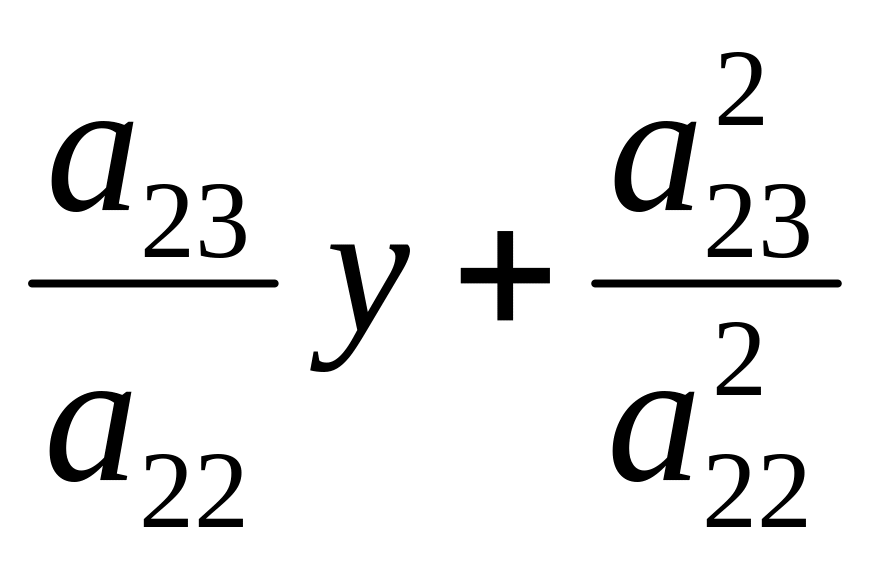

Обозначим и свернём скобки.

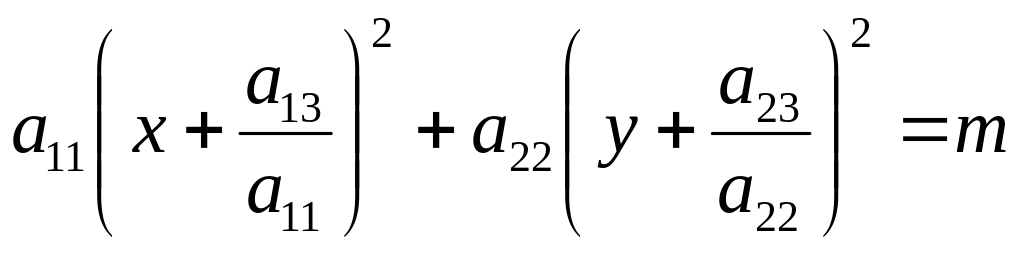(14)

После преобразования координат, сделанного по формулам 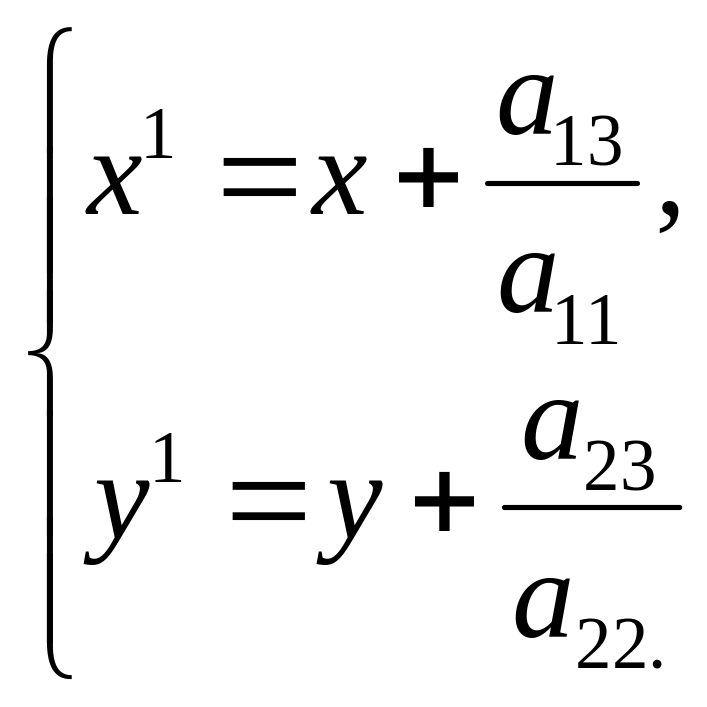(15), получим уравнение (16). Возможны случаи:

1) а₁₁, а₂₂ и m – числа одного знака. Разделим обе части на m и обозначим , . Уравнение (16) запишется (17). Это уравнение определяет эллипс.

2) а₁₁, а₂₂ – числа одного знака, m имеет противоположный знак. Разделим обе части уравнения (16) на (m) и обозначим  ,  . Уравнение (16) будет иметь вид (18)

Это уравнение определяет пустое множество точек. Его называют мнимым эллипсом.

3) а₁₁, а₂₂ – числа разных знаков, m  0. Пусть m и а₁₁ одного знака. Обозначим ,  . Тогда уравнение (16) запишется (19)

Это уравнение определяет гиперболу.

4) а₁₁, а₂₂ – числа разных знаков, m = 0. Пусть а₁₁  0, а₂₂  0. Обозначим , . Уравнение (16) преобразуется к виду . (20) Разложив левую часть на множители, получим . Отсюда либо , либо . Эти уравнения определяют пару пересекающихся прямых.

5) а₁₁, а₂₂ – числа одного знака, m = 0. Можно считать, что а₁₁ и а₂₂ положительны. Обозначим , . Уравнение (16) перепишется (21)

Это уравнение определяет единственную точку х¹ = у¹ = 0. Говорят, что линия Г распадается на пару мнимых прямых, пересекающихся в действительной точке.

II. а₁₁ = 0, а₂₂  0. Уравнение (13) преобразуется к виду

.

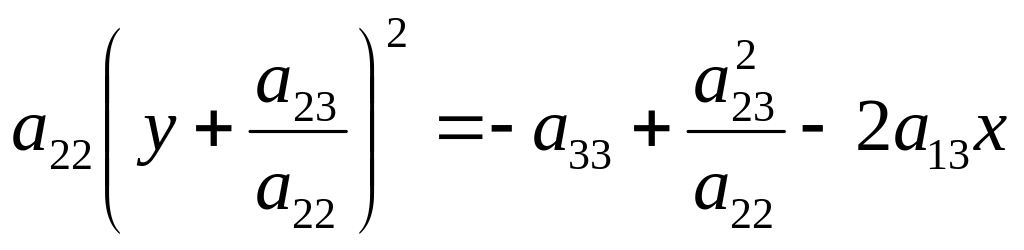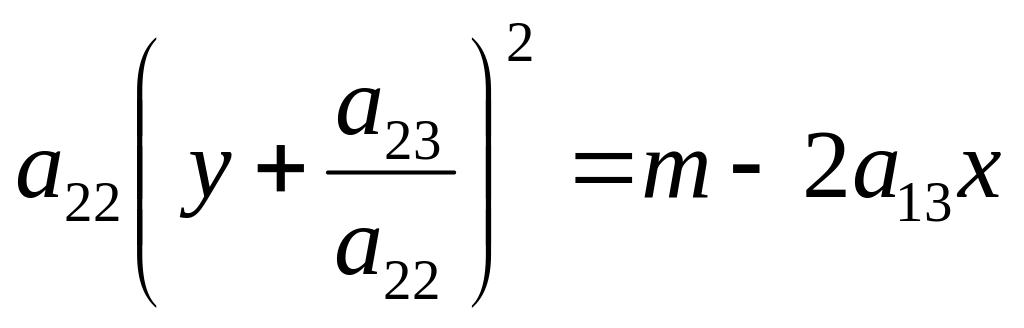Обозначим m = , получим уравнение (22)

Возможны случаи:

1) а₁₃  0. Сделаем преобразование координат 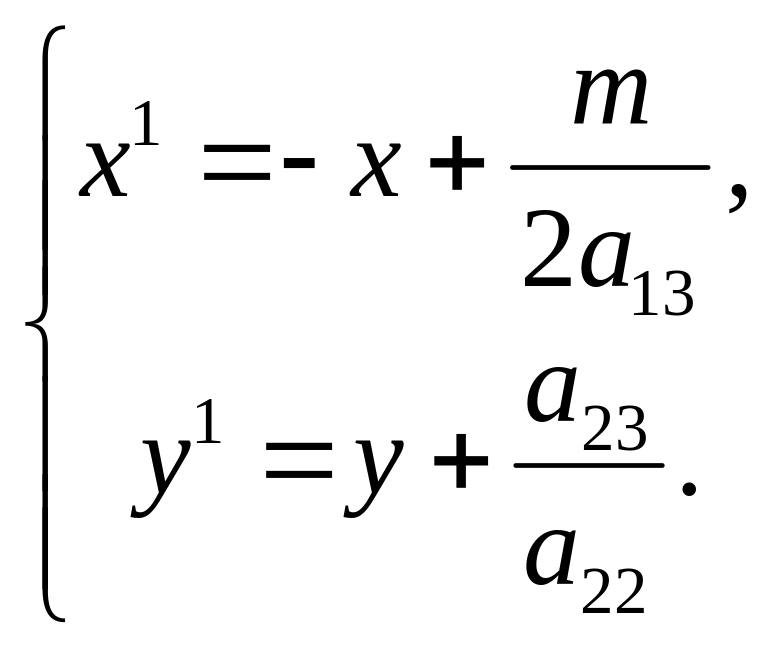Если обозначить р = , то получим уравнение (у¹)² = 2рх. (23) Это уравнение определяет параболу.

2) а₁₃ = 0. Сделаем преобразование координат 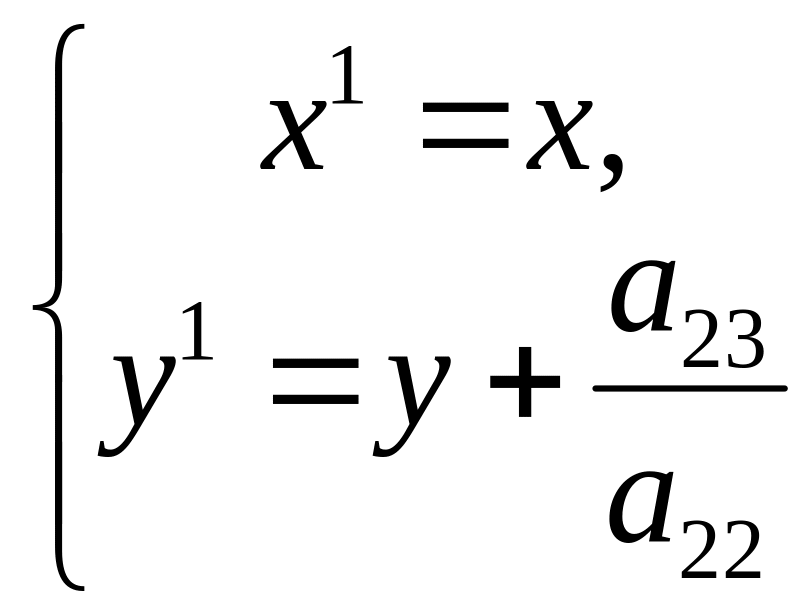. Получим уравнение а₂₂(у¹)² = m. Возможны случаи а) а₂₂ и m одного знака. Обозначим . Получим уравнение (у¹)² = а² , а  0 (24). Это уравнение определяет пару различных действительных параллельных прямых.

б) а₂₂ и m разных знаков. Получим уравнение (у¹)² =  а² , а  0 (25)

Это уравнение определяет пустое множество точек. Линия Г называется парой мнимых параллельных прямых.

в) m = 0. Получим уравнение (у¹)² = 0. (26) Оно определяет пару совпавших прямых.

Итак, доказана

Теорема 9. Если линия второго порядка задана в прямоугольной системе координат уравнением (9), то с помощью преобразования координат её уравнение можно привести к одному из следующих девяти видов:

(эллипс); (мнимый эллипс);

(гипербола); (пара пересекающихся прямых);

( пара мнимых прямых, пересекающихся в действительной точке);

у² = 2рх (парабола) у² = а², а  0 (пара различных

параллельных прямых);

у² =  а², а  0 (пара мнимых параллельных прямых);

у² = 0 (пара совпавших прямых).

Из теоремы 9 следует метрическая классификация линий второго порядка: существует ровно девять типов линий второго порядка.