5.1. Лінійні багатофакторні моделі
Вплив багатьох чинників на результативну змінну може бути описаний лінійною моделлю
,
(5.1)
де
– точні фактичні значення досліджуваної
(залежної, пояснюваної) змінної, показника
або регресанду;
,
,
…,
– незалежні (пояснюючі) змінні, фактори
або регресори;
,
,
,
…,
– невідомі параметри моделі;
– випадкова складова регресійного
рівняння,
– кількість фокторів у моделі.
Рівняння
(5.2)
буде
оцінкою моделі (5.1) , якщо
– теоретичні значення досліджуваного
показника,
,
,
,
…,
– оцінки точних значень параметрів
,
,
,
…,
.
Функція (5.2) є лінійною відносно незалежних змінних і параметрів моделі, але саме лінійність за параметрами є більш суттєвою, оскільки це пов'язано з методами оцінювання параметрів. Випадкова складова є результативною дією всіх неконтрольованих випадкових факторів, що зумовлюють відхилення реальних значень досліджуваного показника від аналітичних (обчислених на підставі обраної регресійної залежності).
Лінійні зв'язки не вичерпують усіх можливих форм залежності між показниками. Тому при дослідженні конкретного економічного явища першочерговим завданням є пошук найточнішої аналітичної форми опису статистичного зв'язку між його показниками. Певна форма залежності повинна мати відповідне економічне обгрунтування. Якщо вигляд залежності встановити важко, то за перше наближення до моделі все ж обирають лінійну залежність.
Звичайним математичним підходом до розв'язання задач є відокремлення специфічних класів задач або зведення задач до деякого класу і застосування відповідних методів розв'язування. Оскільки дослідження лінійних функцій має незаперечні переваги перед іншими класами функцій, то нелінійні функції намагаються передусім звести до лінійних.
Наприклад,
степенева функція
після логарифмування набуває вигляду
і після заміни
є лінійною відносно параметрів
,
,
,
…,
.
Показникова
функція
після логарифмування набуває вигляду
і після заміни
стає
лінійною відносно нових параметрів
,
,
,
…,
.
Гіперболічна
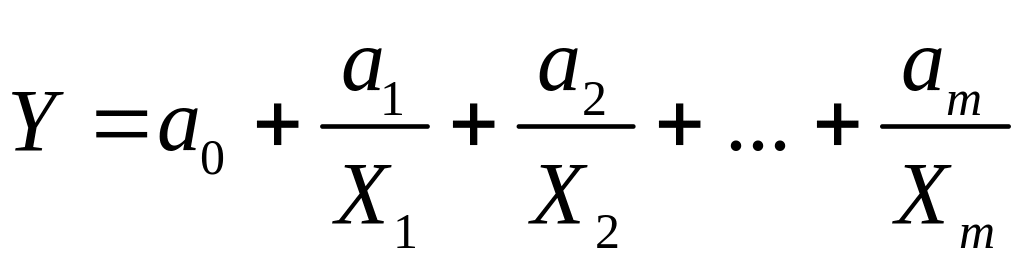функція за допомогою заміни змінних
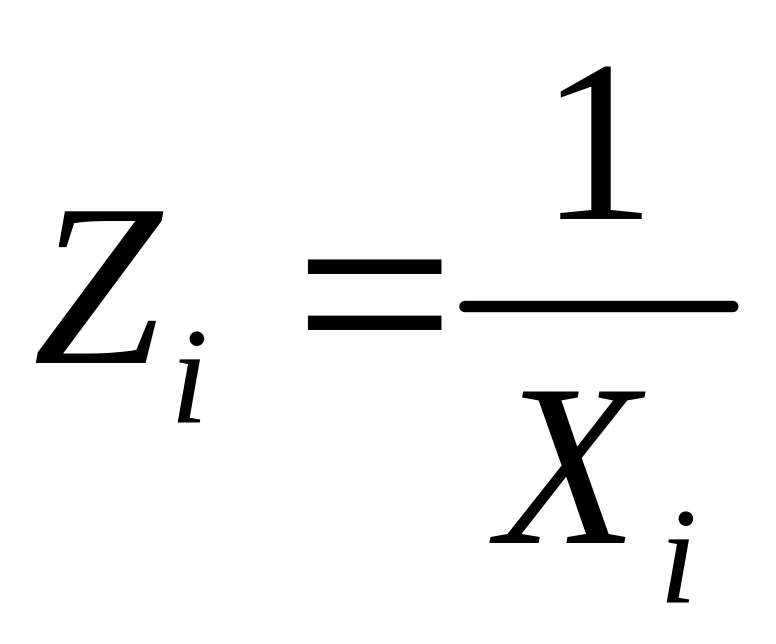зводяться до лінійного вигляду
.
Квадратична
функція
зводиться до лінійної
за допомогою заміни
.
Зауважимо, що в сучасному економічному аналізі існують залежності, які не зводяться до лінійних елементарними перетвореннями, однак їх параметри
можна легко розрахувати спеціальними спрощеними методами.
Оскільки найпоширенішими в економетричному моделюванні є лінійні функції, обгрунтування економетричних методів розглядають, як правило, на базі лінійних моделей. Отже, предметом наших досліджень буде узагальнена багатофакторна лінійна регресійна модель (5.2).
Узагальнена регресійна модель справджується для всієї генеральної сукупності, а похибка регресії має певний закон розподілу. На практиці мають справу з вибірковою моделлю, тобто з такою, яка побудована для деякої вибірки. Параметри вибіркової моделі є випадковими величинами, а їх математичне сподівання дорівнює параметрам узагальненої моделі. Щоб визначити параметри узагальненої моделі, необхідно за вибіркою отримати якомога кращі їх оцінки, тобто значення, найближчі до параметрів узагальненої моделі. З цією метою використовують метод найменших квадратів (МНК), який для багатофакторної лінійної моделі зручно застосовувати у матричній формі.
Розглянемо, наприклад, лінійну модель двохфакторної регресії
.
(5.3)
Система нормальних рівнянь в матричній формі записується як
,
(5.4)
де
через
позначено матрицю початкових даних;
через
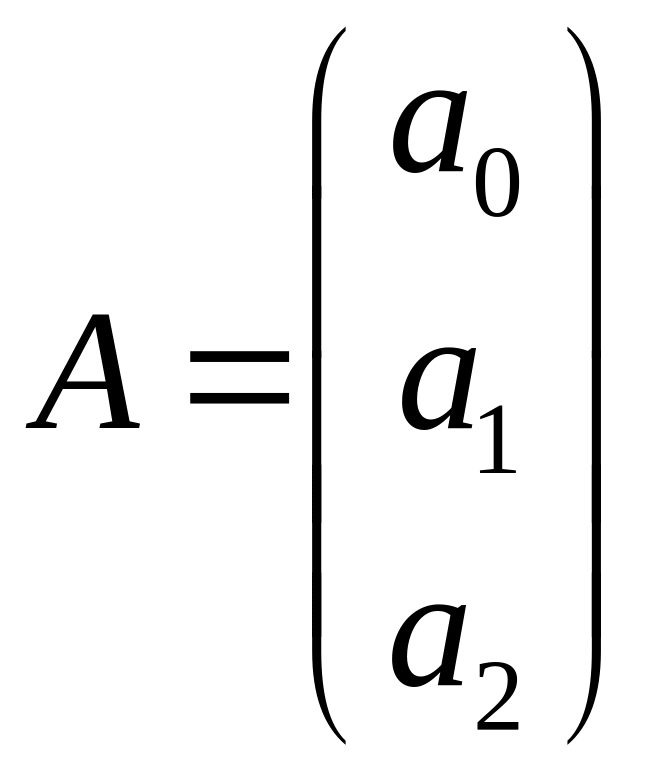– вектор-стовпець невідомих оцінок
параметрів; через
– вектор-стовпець спостережених значень
досліджуваного показника.
Оскільки
зазвичай
передбачається, що рівняння регресії
(5.3) має вільний член, тобто
,
то для того, щоб отримати оцінку параметра
,
розширюємо матрицю
урахуванням в неї змінної
.
Тому
перший стовпець матриці початкових
даних складається
з одиниць, а два інші стовпці містять
спостереження над змінними
і
.
Згідно
МНК рівняння (5.4) треба помножити зліва
на транспоновану матрицю
початкових даних:
.
Матрицю
називають інформаційною
матрицею
задачі.
Її можна обчислити за формулою
.
Коректне
застосування МНК передбачає відсутність
суттєвої мультиколінеарності факторів.
В цьому випадку інформаційна матриця
є не виродженою і має обернену
,
множення останньої рівності на яку дає
формулу для оцінки вектору параметрів
моделі за МНК
.
(5.5)
Слід зауважити, що формула (5.5) знаходження оцінок параметрів двохфакторної лінійної моделі (5.3) є справедливою для випадку будь-якого скінченного числа факторів.
Для випадку множинної регресії вводять деякі нові показники точності її підбору та критерії її перевірки.
Множинний
коефіцієнт кореляції
дорівнює парному коефіцієнту кореляції
між фактичними
і теоретичними
значеннями
змінної
і характеризує ступінь точності підбору
моделі. Він обчислюється за формулою
.
(5.6)
Для знаходження множинного коефіцієнта кореляції застосовують також модифікації формули (5.6) у вигляді
,
,
.
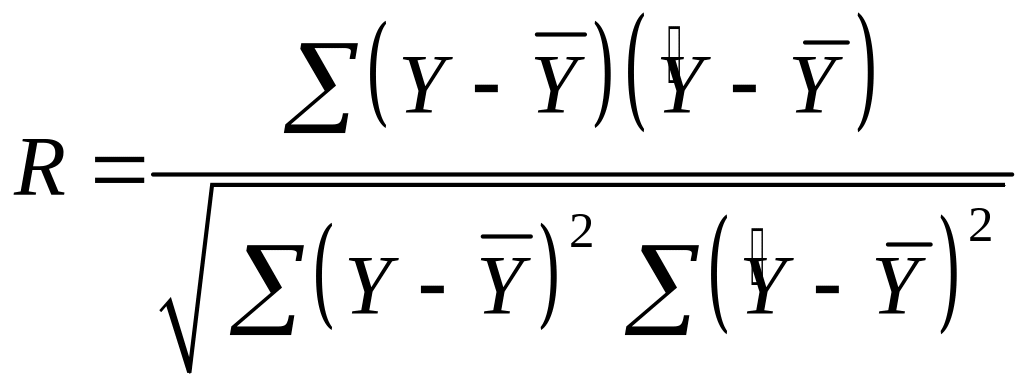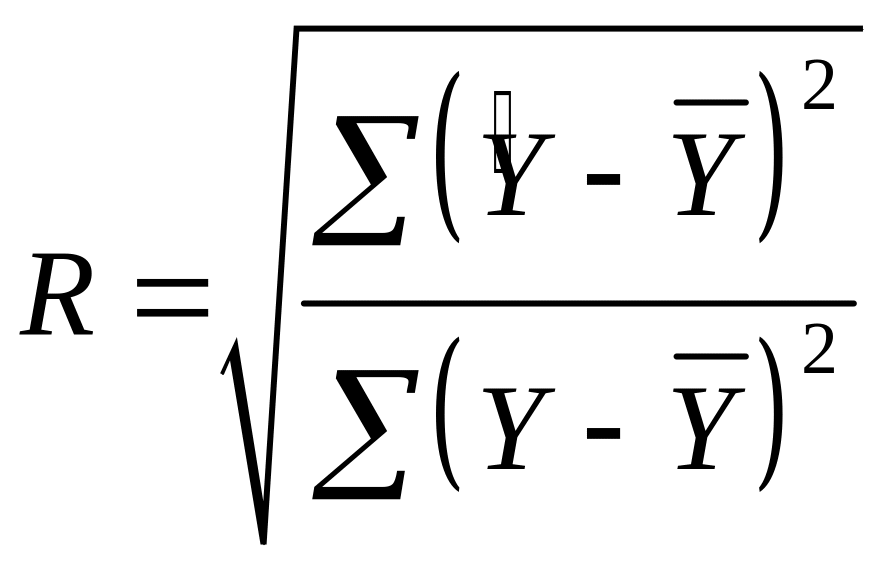Для одержання висновків про практичну значущість синтезованої в аналізі моделі показникам тісноти зв'язку дається кількісна оцінка на основі шкали Чеддока (табл. 4.1).
Довірчий інтервал для генерального множинного коефіцієнта кореляції має вигляд
,
(5.7)
де
,
– кількість спостережень,
– число факторів,
– рівень значущості, критичне значення
знаходять
за таблицями Стьюдента (додаток 5).
Коефіцієнт
детермінації
характеризує частку загальної дисперсії
відносно середнього
,
яку можна пояснити побудованим рівнянням
регресії.
При вивченні кореляційних залежностей показників комерційної діяльності в умовах переваги малого ы середнього бізнесу аналізу піддаються порівняно невеликі по складу одиниць сукупності. При чисельності об'єктів аналізу до 30 одиниць виникає необхідність перевірки параметрів рівняння регресії на їх типовість. При цьому здійснюється перевірка, наскільки розрахункові параметри характерні для відображення всього комплексу умов. Перевірка проодиться за
критерієм
Фішера і
критерієм
Стьюдента.
Критерій
Фішера:
фактичне значення
статистики,
яке обчислюють за формулою
,
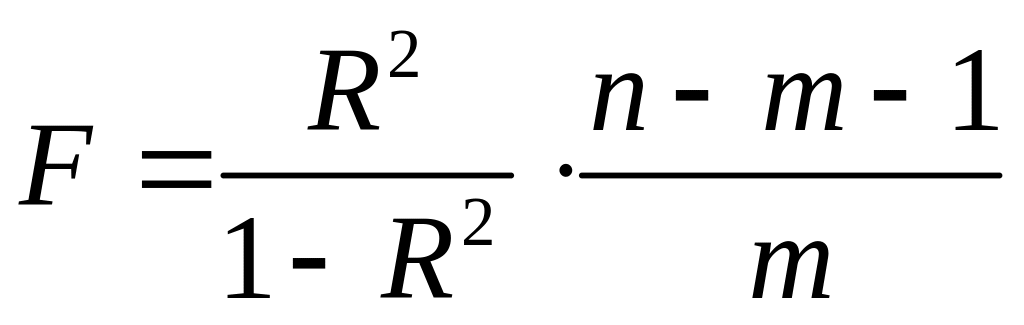порівнюють з критичним
(додаток 1). Якщо
,
то рівняння регресії є значущим,
коефіцієнт множинної кореляції значуще
відрізняється від нуля, модель адекватно
описує зв'язок між показником
і
факторами
,
,
…,
.
Критерій
Стьюдента:
обчислюють
величину
статистики
,
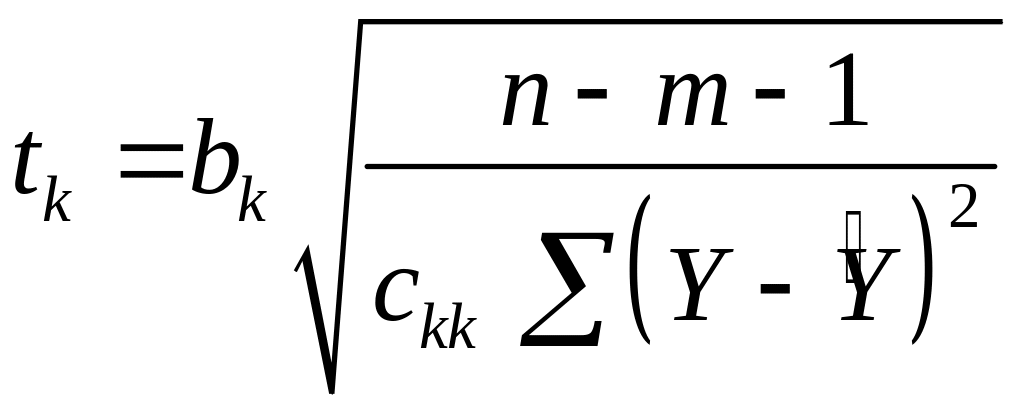де
– діагональний елемент матриці
.
По таблицях критичних точок Стьюдента
знаходять критичне значення
(додаток 2). Якщо
,
параметр
значуще відрізняється від нуля, між
показником
і фактором
існує лінійна залежність.
Довірчий інтервал для параметра рівняння складе
,
.
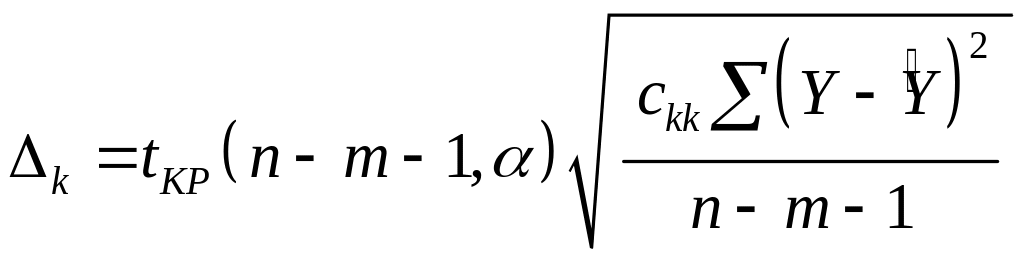(5.8)
Важливим показником адекватності побудованої моделі є величини відносних відхилень розрахункових рівнів показника від його фактичних значень. Вважають, якщо величина відносних відхилень для більшості вимірів не перевершує 5%, то модель є адекватною фактичним даним.
Коефіцієнт
еластичності
по
є безрозмірним показником, що визначає
вплив цього фактору на показник
.
(5.9)
Якщо
зміниться на 1%, то
зміниться на
%.
Оскільки для лінійної регресії
коефіцієнт еластичності залежить від
:
,
то найчастіше
обчислюють
коефіцієнт еластичності для середнього
.
Прогнозування:
припустимо, ми хочемо поширити нашу
модель на інші значення факторних
змінних і поставити проблему прогнозування
середнього значення
,
що відповідає деякому даному значенню
змінних
. Причому ці нові значення
можуть лежати як між вибірковими
спостереженнями, так і поза відповідними
інтервалами. Точковий прогноз представляє
із себе обчислене по рівнянню (5.2) значення
.
Інтервальний прогноз складає довірчий
інтервал, що покриває із заданою
надійністю
очікувану величину
:
.
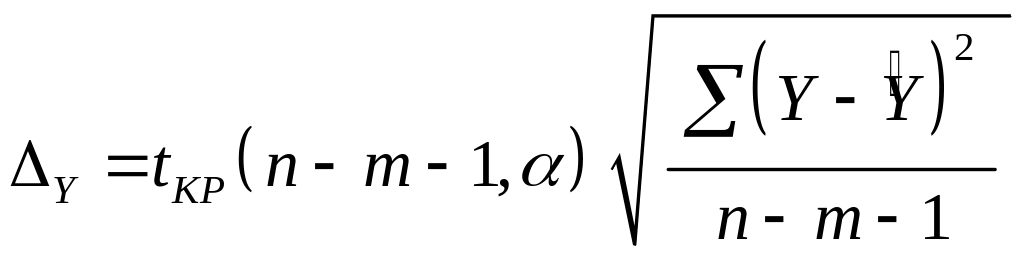(5.10)
Приклад
5.1.
Побудувати
лінійну двохфакторну модель регресії
взаємозв'язку товарообігу підприємства
(тис.грн.)
від
витрат на рекламу (тис.грн.)
і кількості глядачів каналу (тис.чол.)
за даними табл. 5.1.
Таблиця 5.1 – Дані приклада 5.1
|
60 |
45,1 |
86,5 |
51,1 |
58,1 |
43,6 |
55,9 |
76,6 |
32,3 |
59,6 |
|
0,88 |
0,77 |
1,8 |
0,84 |
1,12 |
0,66 |
0,86 |
1,27 |
0,68 |
0,86 |
|
0,91 |
1,68 |
1,29 |
1,02 |
0,88 |
0,82 |
1,09 |
1,52 |
0,71 |
1,1 |
Розв’язок: Запишемо матриці і
Інформаційну матрицю можна обчислити безпосередньо як добу-
ток двох матриць (наприклад, використовуючи функції пакету EXCEL):
.
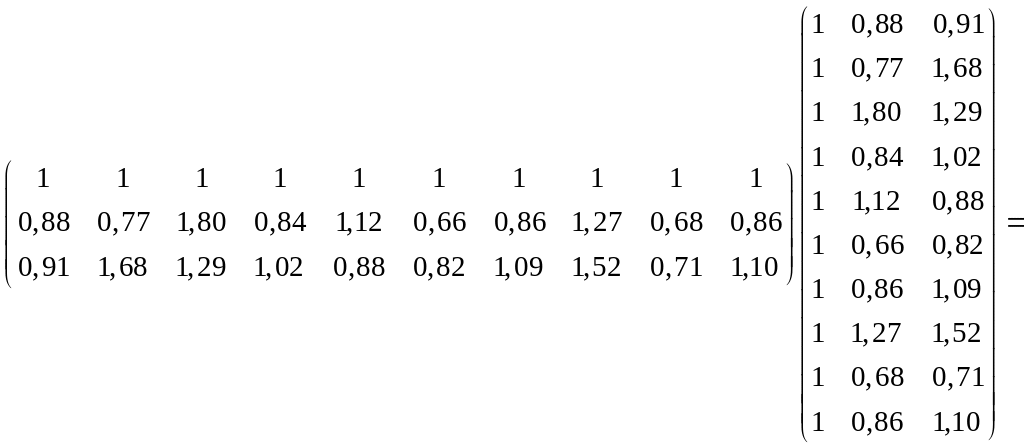
Отже,
.
Для
визначення вектора
коефіцієнтів рівняння регресії (5.3)
знаходимо обернену матрицю
і вектор
:
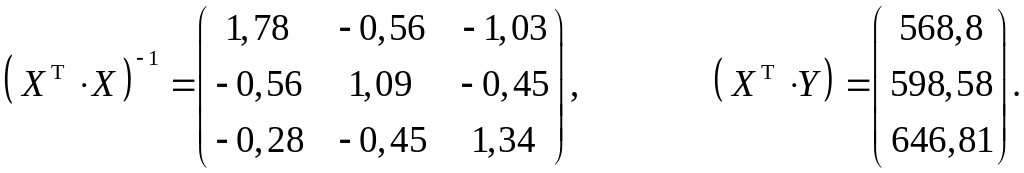
Вектор коефіцієнтів рівняння регресії визначаємо за формулою (5.5)
.
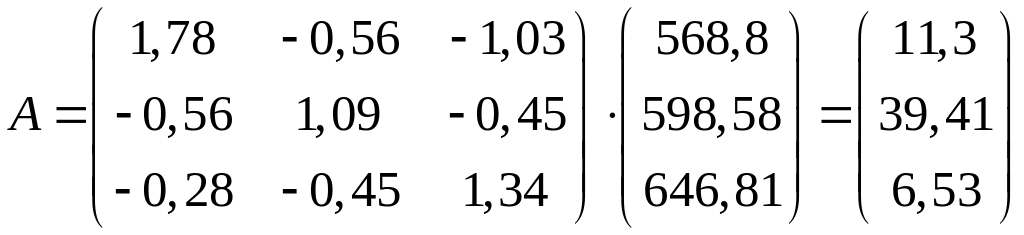Тоді, рівняння регресії (5.3) має вигляд
.
(5.11)
Після побудови регресійної моделі потрібно оцінити її практичну значущість. Розрахунок залишкової дисперсії і середньої помилки апроксимації дамо в таблиці 5.2.
Таблиця 5.2 – Розрахунок і
|
|
|
|
|
60 |
51,92 |
8,08 |
65,24 |
13,46 |
45,1 |
52,62 |
7,52 |
56,49 |
16,67 |
86,5 |
90,66 |
4,16 |
17,32 |
4,81 |
51,1 |
51,07 |
0,04 |
0,001 |
0,07 |
58,1 |
61,19 |
3,09 |
9,52 |
5,31 |
43,6 |
42,67 |
0,94 |
0,88 |
2,14 |
55,9 |
52,31 |
3,59 |
12,89 |
6,42 |
76,6 |
71,28 |
5,32 |
28,34 |
6,95 |
32,3 |
42,74 |
10,44 |
108,89 |
32,31 |
59,6 |
52,38 |
7,22 |
52,19 |
12,12 |
Разом |
|
|
351,76 |
100,26 |
Дисперсія залишкова |
50,25 |
10,03 |
||
Середнє квадратичне відхилення |
7,09 |
|
||
Залишкова
дисперсія
.
Відсоток відхилення по окремих значеннях
вибірки змінюються від 0,07
%
до 32,31
%.
Середня помилка апроксимації для
рівняння регресії в цілому складає
.
Для
обчислення множинного коефіцієнта
кореляції розрахуємо допоміжні величини
;
;
;
;
.
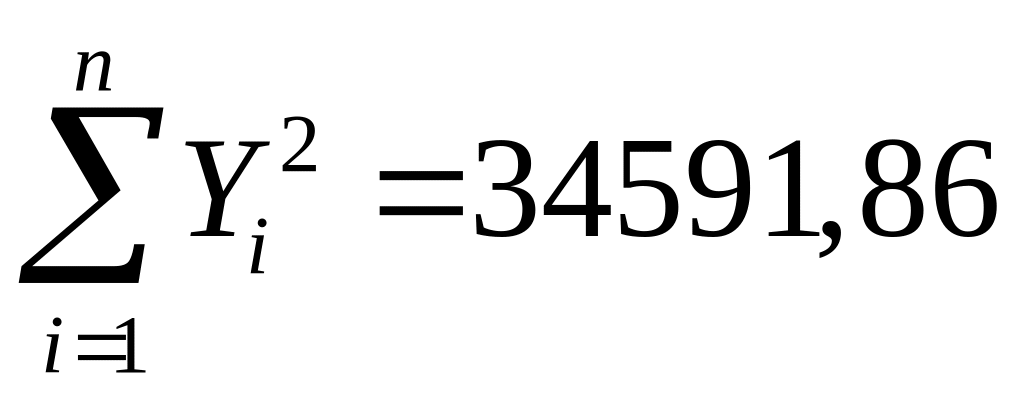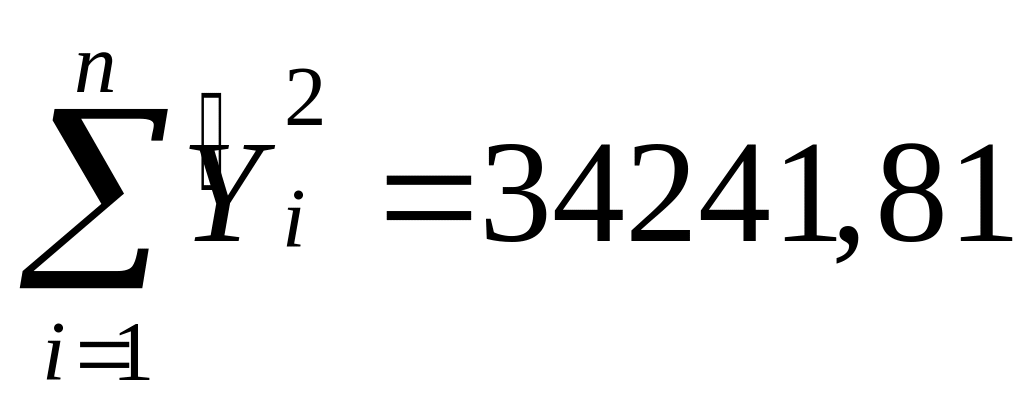Значення множинного коефіцієнта
кореляції
свідчить про тісний лінійний кореляційний
зв'язок
з
і
.,
а також про
задовільну узгодженість теоретичних
даних з фактичними.
Зауваження. Регресійний та дисперсійний аналізи лінійної регресії можна провести використовуючи опцію «Регресія» пакета EXCEL (рис. 5.1).
ВЫВОД ИТОГОВ |
|
|
|
Регрессионная статистика |
|
Множественный R |
0,918075435 |
R-квадрат |
0,842862505 |
Нормированный R-квадрат |
0,797966078 |
Стандартная ошибка |
7,088771776 |
Наблюдения |
10 |
Дисперсионный анализ |
|
|
|
|
|
|
df |
SS |
MS |
F |
Значимость F |
Регрессия |
2 |
1886,761203 |
943,3806015 |
18,77348729 |
0,001538082 |
Остаток |
7 |
351,7547971 |
50,25068529 |
|
|
Итого |
9 |
2238,516 |
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
|
Y-пересечение |
11,29995504 |
9,465548756 |
1,193798197 |
0,271439463 |
-11,0825111 |
33,68242118 |
|
Переменная X 1 |
39,40886688 |
7,393996433 |
5,329846617 |
0,001087621 |
21,9248436 |
56,89289015 |
|
Переменная X 2 |
6,529771887 |
8,200711003 |
0,796244604 |
0,452043676 |
-12,86182823 |
25,921372 |
|
ВЫВОД ОСТАТКА |
|
|
|
|
|
|
|
|
|
|
|
Наблюдение |
Предсказанное Y |
Остатки |
Стандартные остатки |
|
|
1 |
51,92185031 |
8,078149689 |
1,292150609 |
|
|
2 |
52,61479931 |
-7,514799308 |
-1,20203919 |
|
|
3 |
90,65932115 |
-4,159321155 |
-0,665309455 |
|
|
4 |
51,06377054 |
0,036229456 |
0,005795128 |
|
|
5 |
61,1840852 |
-3,084085205 |
-0,493318734 |
|
|
6 |
42,66422013 |
0,935779871 |
0,149683848 |
|
|
7 |
52,30903191 |
3,590968087 |
0,574397824 |
|
|
8 |
71,27446924 |
5,325530756 |
0,85185198 |
|
|
9 |
42,73412256 |
-10,43412256 |
-1,669003218 |
|
|
10 |
52,37432963 |
7,225670368 |
1,155791206 |
|
|
Рисунок 5.1 – Результати регресійного і дисперсіного аналізу
За
таблицями знаходимо критичне значення
критерію Стьюдента (додаток 2)
;
.
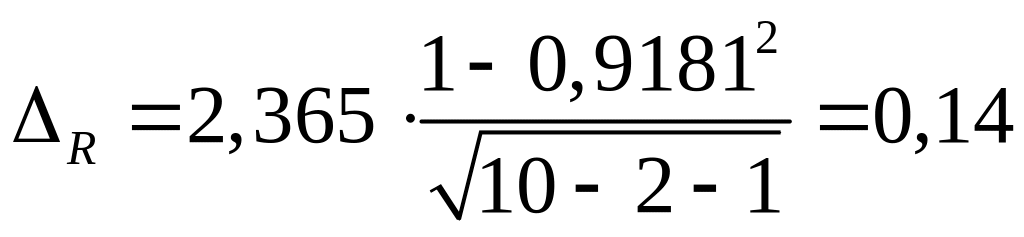Довірчий інтервал для множинного
коефіцієнта кореляції має вигляд
.
Оскільки множинний коефіцієнт кореляції
не може бути більше 1, то інтервал приймає
вигляд
.
З помилкою в 5% мо-
жна стверджувати, що фактичний коефіцієнт кореляції не менше ніж 0,78.
Коефіцієнт
детермінації
показує, що 84,29
% дисперсії показника
можна
пояснити за допомогою моделі залежності
від
і
.
статистики
дорівнює
.
Критичне значення при
складе
.
Оскільки
,
то побудовану модель можна вважати
адекватною.
Змістовне значення параметрів знайденої моделі наступне:
якщо фактор зміниться на одиницю свого вимірювання, то показник в середньому зміниться на
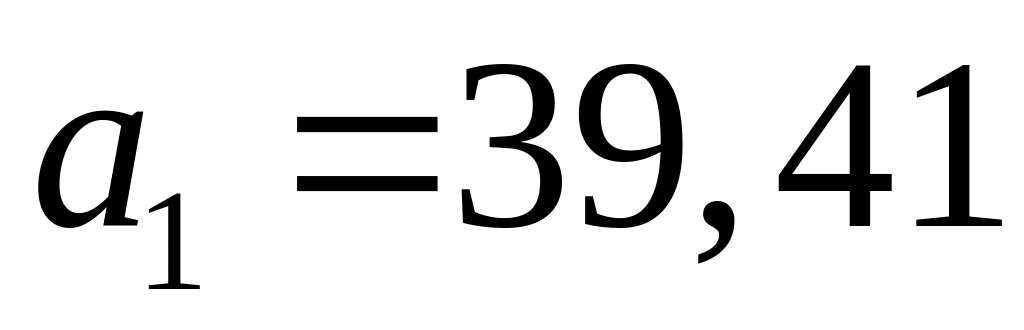одиниці свого вимірювання за умови, що
чинник
залишається без змін;аналогічно, якщо фактор змінитися на одиницю свого вимірювання, то показник зміниться на
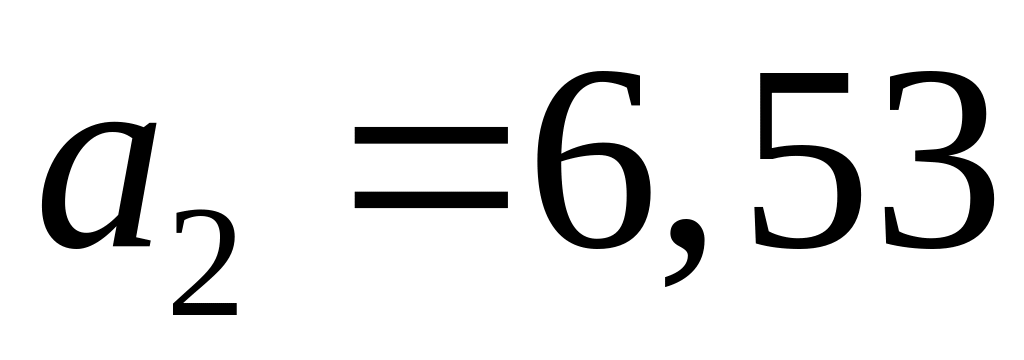одиниць свого вимірювання при умові
незмінності фактору
.
Таким чином, зміна витрат на рекламу на 1 тис. грн. призведе до зміни в тому ж напряму товарообігу в середньому на 39,41 тис. грн.; зміна кількості глядачів каналу на 1 тис. призведе до зміни в тому ж напряму товарообігу підприємства на 6,53 тис. грн.