Модель розподільчої задачі

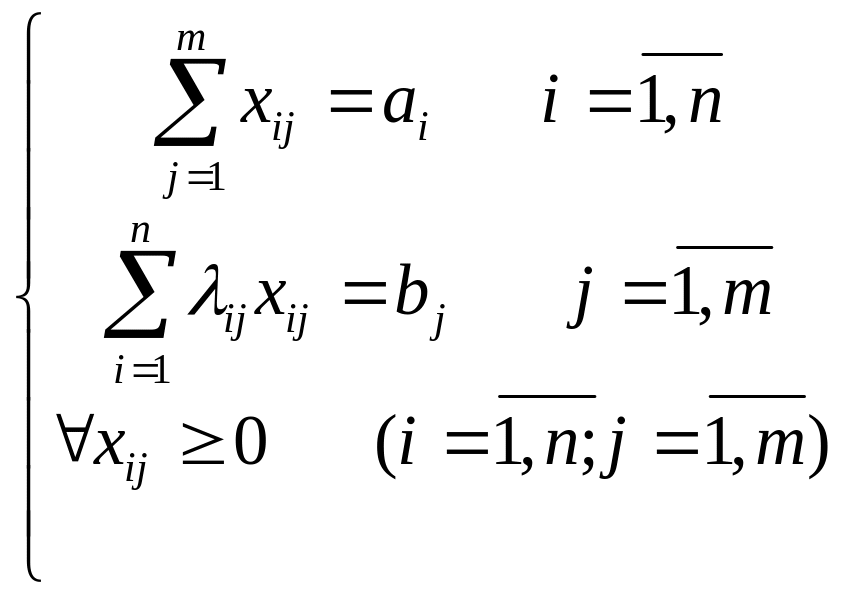(7)

де - це кількість робіт j – го виду, i – м виконавцем.

Етапи розв’язання розподільчої задачі

І. Перетворення розподільчої задачі в транпортну задачу:

1. вибір базового ресурсу і розрахунок нормованих продуктивностей ресурсів α_i:

2. перерахунок запасу робочого ресурсу виконавців :

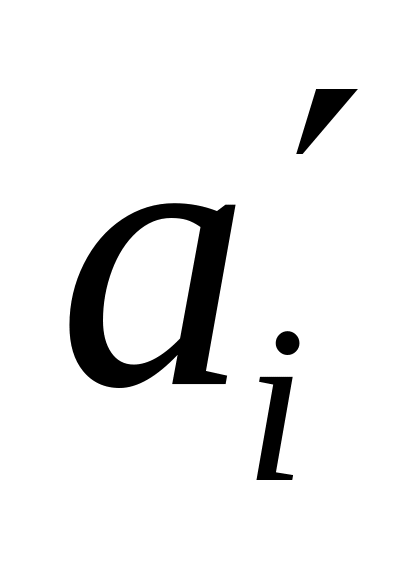[од. ресурсу];

3. перерахунок планового завдання :

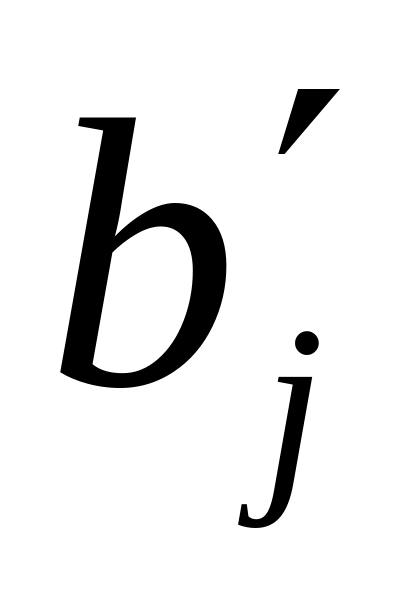4. перерахунок собівартості робіт:

ІІ. Перевірка балансу перерахованих параметрів і побудова транспортної матриці.

ІІІ. Пошук оптимального розв’язку транспортної задачі .

IV. Перетворення оптимального розв’язку транспортної задачі в оптимальний розв’язок розподільчої задачі, причому перехід виконується за формулою:

[од. ресурсу],

де і - відповідні елементи розв’язку розподільчої задачі і транспортної задачі.

V. Визначення кількості робіт, відповідно оптимальному розв’язку розподільчої задачі Х^*:

VI. Визначення цільової функції розподільчої задачі Z згідно з (7).

2. Приклад вирішення задачі типу тз.

На фабриці працюють три типи ткацьких верстатів, які можуть випускати чотири види тканин. Відомі наступні дані про виробничій процес:

• продуктивність верстатів по кожному виду тканин, м/год

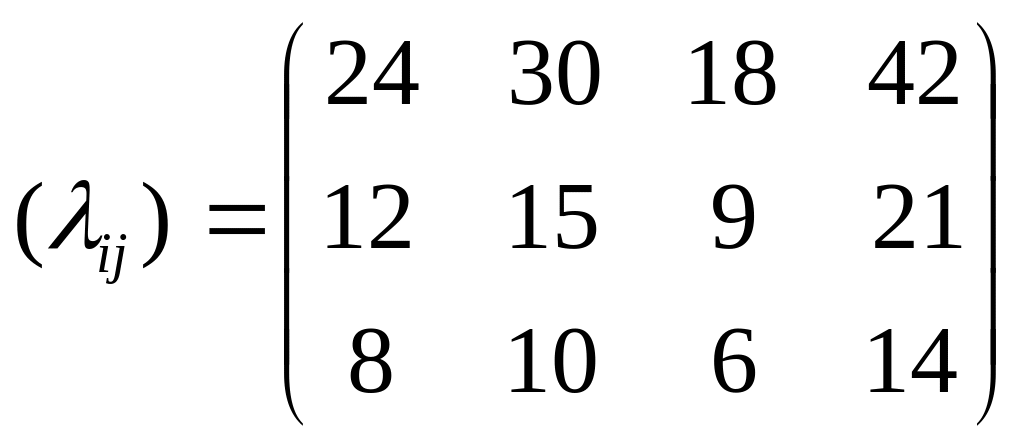
• собівартість тканини, грн./м

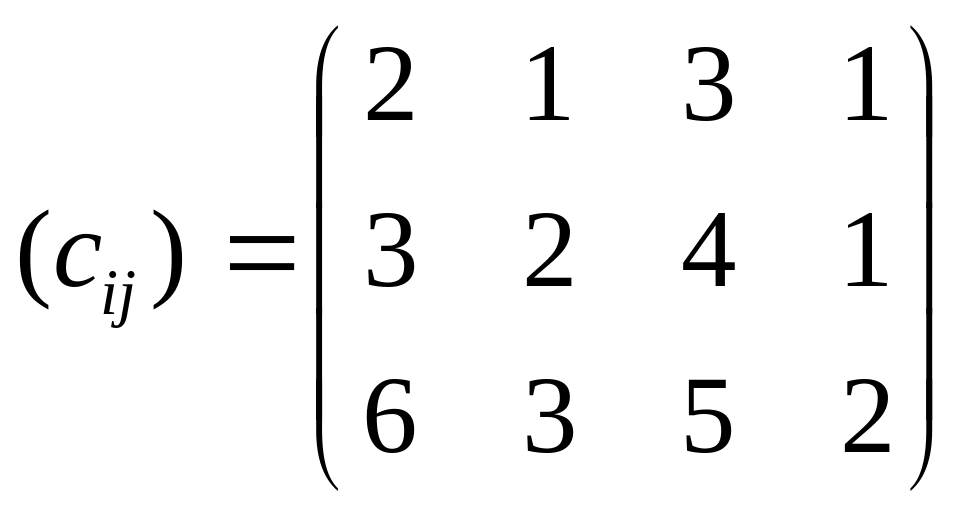
• ресурси робочого часу верстатів (a_i): 90, 220, 180 год;

• запланований об’єм випуску тканин (b_j): 1200, 900, 1800, 840 м.

Вимагається розподілити випуск тканини по верстатах так, щоб мінімізувати загальну собівартість виробництва тканин.

Питання для самоконтролю.

• Чому транспортну задачу вирішують іншими методами, якщо це задача лінійного програмування?

• Яка транспортна задача називається закритою?

• Що робити якщо транспортна задача відкрита?

• Дайте означення опорного плану транспортної задачі.

• Коли опорний план транспортної задачі не вироджений?

• Що робити, якщо опорний план транспортної задачі вироджений?

• Дайте означення оптимального опорного плану транспортної задачі.

• Сформулюйте необхідні і достатні умови існування розв’язку транспортної задачі.

• Як построїти потенціали строк і стовпців?

• В чому полягає метод північно-західного кута?

• В чому полягає метод найменших витрат?

• Як визначити, що опорний план оптимальний?

• Дайте означення циклу перерозподілу поставок.

Тема 4. Теорія двоїстості та аналіз лінійних моделей оптимізаційних задач. Лекція 10. Тема лекції: Двоїста задача лінійного програмування

Мета: ознайомити студентів з методами розв’язання двоїстих задач лінійного програмування, показати взаємозв’язок прямої та двоїстої задач.

План лекції

1. Математичні моделі двоїстих задач.

2. Основні теореми теорії двоістості.

3. Взаємозв’язок розв’язків прямої та двоїстої задач.

Література:

1. Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.

2. Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.

3. Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.

4. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.