Тема 2. Загальна задача лінійного програмування та деякі з методів її розв’язування Лекція 6 Тема лекції: Розв’язання задач лп симплекс-методом (продовження)
Мета: ознайомити студентів з методами розв’язання задач ЛП симплекс – методов із стандартним базисом, симплекс-методом зі штучним базисом.
План лекції
Правило уникнення зациклювання при застосуванні симплекс-методу.
Метод штучної базиси розв’язування задач ЛП.
Приклад вирішення задачі ЛП методом штучної бази.
Література:
Лавріненко Н.М., Латинін С.М., Фортуна В.В., Безкровний О.І. Основи економіко-метематичного моделювання: Навч. Посіб. - Львів: «Магнолія 2006», 2010.- 540с.
Іванюта І. Д. Практикум з математичного програмування: Навчальний посібник / І. Д. Іванюта, В. І. Рибалка, І. А. Рудоміно-Дусятська. – К.: «Слово», 2008. - 296 с.
Кучма М. І. Математичне програмування: приклади і задачі: Навчальний посібник / М.І. Кучма. – Львів: «Новий Світ - 2000», 2006. - 344 с.
Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1993. – 336 с.
4. Правило уникнення зациклювання при застосуванні симплекс-методу.
Якщо на будь якому етапі розрахунків виникає невизначеність у виборі ключового рядка, тобто виявляється кілька однакових мінімальних симплексних відношень, то необхідно вибирати рядок, для якого відношення елементів наступного стовпчика, що не входить у базис, до відповідних елементів ключового стовпчика є найменшим. При цьому ділення необхідно виконувати і на від’ємні елементи, тобто отримані відношення можуть бути від’ємними.
Якщо, при цьому знову виявляються однакові мінімальні симплексні відношення, то складають відношення елементів наступного стовпчика, і так роблять доти, доки ключовий рядок не визначиться однозначно.
Приклад 2. Вирішити задачу ЛП
за умов
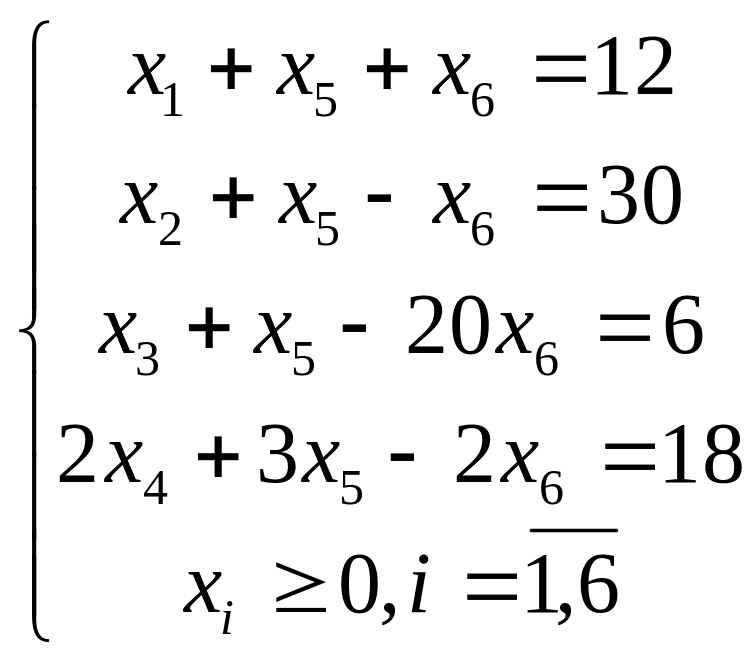
5. Метод штучної базиси розв’язування задач лп.
Застосовується у тих випадках, коли в вихідній задачі ЛП, яка записана у канонічному вигляді, в системі обмежень немає необхідної кількості одиничних ортогональних незалежних векторів Pj, тобто важко вказати початковий опорний план.
М-метод полягає у використанні правил симплекс – методу до так званої задачі ЛП. Вона отримується із початкової додованням до лівої частини системи рівнянь таких штучних одиничних векторів з відповідними невід’ємними штучними змінними, щоб знову отримати m одиничних ортогональних лінійно незалежних векторів.
У цільовій функції задачі ЛП штучні змінні мають коефіцієнт - М (f(x)→max) або +М (f(x)→min), де під М ми розуміємо досить велике додатне число.
При розв’язанні цієї задачі симплекс-методом оцінки Δj будуть залежити від М. Для порівняння оцінок, треба пам’ятати, що М – достатньо велике додатне число, тому із базису будуть виключатися у першу чергу штучні вектори.
Якщо із базису всі штучні вектори вийшли, то ми отримали вихідну задачу.
Якщо оптимальний розв’язок М – задачі містить штучні змінні або М – задача нерозв’язна, то початкова задача також нерозв’язна.