Глава IV. Евклидовы пространства.
§1.Вещественное евклидово пространство и его основные свойства.
1. Определение вещественного евклидова пространства.
Определение 1. Вещественное
линейное пространство
называется вещественным евклидовым
пространством, если выполняются следующие
два требования:
1. Имеется правило, посредством которого
любым двум элементам
и
этого пространства ставится в соответствие
вещественное число, называемое их
скалярным произведением и обозначаемое
символом
.
2. Указанное правило подчиняется следующим четырем аксиомам:
1).
- переместительное свойство;
2).
- распределительное свойство;
3).
- сочетательное свойство относительно
числового множителя
;
4).
,
если
- ненулевой элемент,
,
если
- нулевой элемент пространства
.
При введении понятия евклидова пространства мы абстрагируемся не только от природы изучаемых объектов, составляющих пространство , но и от конкретного вида правил формирования суммы элементов, умножения элемента на число и скалярного произведения элементов. Требуется лишь, чтобы эти правила подчинялись восьми аксиомам линейного пространства (гл. 2 §1, п.1) и четырем аксиомам скалярного произведения. Если природа изучаемых объектов конкретизирована и вид перечисленных правил задан, то евклидово пространство называется конкретным, в противном случае – абстрактным.
Рассмотрим примеры конкретных евклидовых пространств.
1). Пространство
всех свободных векторов со скалярным
произведением любых двух векторов,
определяемым как произведение их длин
на косинус угла между ними (по правилам
аналитической геометрии):
. (4.1.1)
2). Бесконечномерное пространство
всевозможных функций
,
определенных и непрерывных на сегменте
со скалярным произведением двух функций
и
,
определенных как интеграл от
до
от их произведения:
. (4.1.2)
3). - мерное линейное арифметическое пространство упорядоченных совокупностей из вещественных чисел со скалярным произведением:
.
(4.1.3)
4). - мерное линейное арифметическое пространство с более общим правилом формирования скалярного произведения. Сформулируем его. Пусть
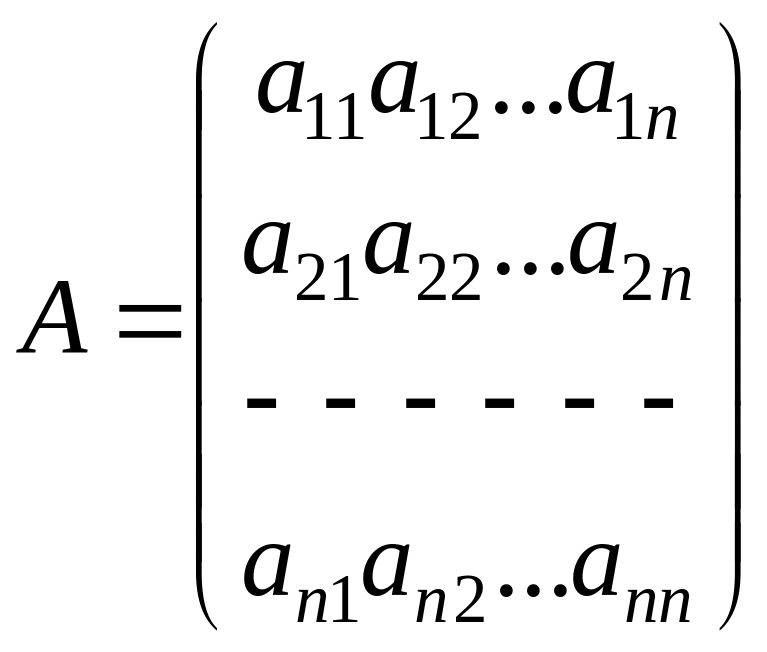(4.1.4)
некоторая квадратная матрица,
- любые два элемента пространства
.
Назовем однородный многочлен:
(4.1.5)
квадратичной формой, порождаемой
матрицей (4.1.4). Квадратичная форма
называется положительно определенной,
если выражение (4.1.5) больше нуля для всех
не равных нулю одновременно. Если же
все
;
т.е.
,
то квадратичная форма (4.1.5) обращается
в нуль. Можно сказать, что положительно
определенная квадратичная форма
обращается в нуль лишь при условии:
.
Потребуем, чтобы матрица (4.1.4) удовлетворяла следующим условиям:
1) Порождала положительно определенную квадратичную форму (4.1.5).
2) Была симметричной (относительно
главной диагонали):
для всех
.
Тогда с помощью матрицы
(4.1.4)
можно определить скалярное произведение
двух элементов
и
следующим соотношением:
(4.1.6)
Правила формирования скалярного произведения, приведенные в примерах 1-4 удовлетворяют четырем системам скалярного произведения, а операции сложения элементов и умножения элемента на число удовлетворяют числам линейного пространства. Поэтому рассмотренные примеры являются линейными евклидовыми пространствами.
2. Простейшие свойства произвольного евклидова пространства. Устанавливаемые в этом пункте свойства справедливы для любого евклидова пространства как конечной, так и бесконечной размерности.
Теорема 4.1. Для любых двух элементов и произвольного линейного пространства справедливо неравенство:
, (4.1.7)
называемое неравенством Коши – Буняковского.
Доказательство. Для любого вещественного числа в силу системы (4.1.5) скалярного произведения выполняется неравенство:
(4.1.8)
Выполняя скалярное перемножение в (4.1.8) с учетом аксиом 1-8 линейного пространства, получим:
(4.1.9)
Квадратный трехчлен относительно
будет неотрицательным, если его
дискриминант не положителен:
,
откуда следует неравенство (4.1.6). Теорема
доказана.
Теперь потребуется ввести понятие нормы (или длины) каждого элемента в произвольном евклидовом пространстве.
Определение. Линейное пространство называется нормированным, если выполнены следующие два требования:
1) Имеется правило, посредством которого
каждому элементу
пространства
ставится в соответствие вещественное
число, называемое нормой (или длиной)
соответствующего элемента и обозначается
символом
2) Указанное правило подчиняется следующим трем аксиомам.
1.
>0,
если
- ненулевой элемент,
,
если
-
нулевой элемент.
2.
- для любого элемента
и для любого вещественного числа
.
3. Для любых двух элементов и справедливо следующее неравенство:
, (4.1.10)
называемое неравенством треугольника
(или неравенством Минковского)
Теорема 4.2. Всякое евклидово пространство является нормированным, если в нем норму любого элемента определить равенством:
(4.1.11)
Доказательство. Достаточно
доказать, что для нормы, определенной
соотношением (4.1.11) справедливы аксиомы
1-3 нормированного линейного пространства.
Справедливость аксиомы 1 вытекает из
аксиомы 4 скалярного произведения.
Справедливость аксиомы 2 следует из
аксиом 1 и 3 скалярного произведения.
Справедливость аксиомы 3 можно установить
на основе неравенства Коши – Буняковского:
.
Перепишем его в виде:
. (4.1.12)
Используя последнее неравенство, а также определение нормы и аксиом 1-4 скалярного произведения, получим:
,
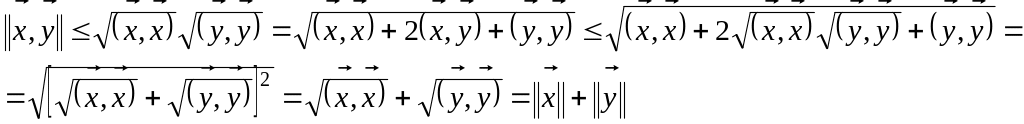т.е. . (4.1.10) Теорема доказана.
Следствие. Во всяком евклидовом пространстве с нормой, определенной выражением (4.1.11) для любых двух элементов и справедливо неравенство треугольника (4.1.10)
В любом вещественном евклидовом
пространстве можно ввести понятие угла
между любыми двумя элементами
и
.
По аналогии с векторной алгеброй будем
называть углом
между элементами
и
такой угол
,
который определяется из равенства:
. (4.1.13)
Определение
по формуле (4.1.13) корректно, так как в
силу неравенства Коши – Буняковского
.
Будем в дальнейшем обозначать евклидово пространство символом .
Два элемента евклидова пространства называют ортогональными, если их скалярное произведение равно нулю:
. (4.1.14)
Сумму
двух ортогональных элементов
и
будем называть гипотенузой прямоугольного
треугольника, построенного на элементах
и
по аналогии с тем, как это имеет место
в векторной алгебре.
Во всяком евклидовом пространстве справедлива теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
, (4.1.15)
так как
.
Этот результат обобщается на случай
любого числа
попарно ортогональных элементов:
.
Обозначим через
следующую сумму:
.
Тогда получим:
(4.1.16)
В заключении запишем норму, неравенство Коши - Буняковского и неравенство треугольника для всех четырех примеров евклидовых пространств, рассмотренных в предыдущем пункте.
1) Пространство всех свободных векторов
:
норма:
- совпадает с длиной вектора; неравенство
Коши – Буняковского:
,
неравенство треугольника:
.
2) Пространство функций: норма:
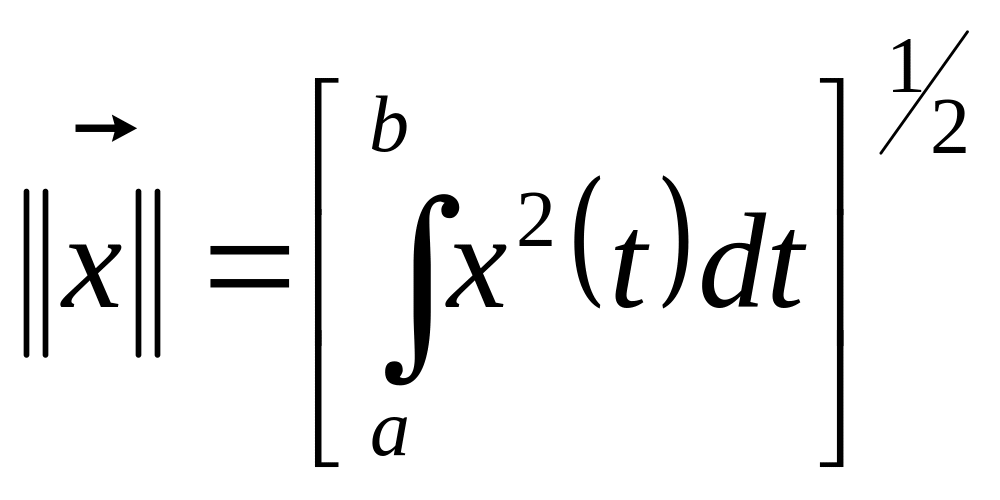неравенство Коши – Буняковского:
;
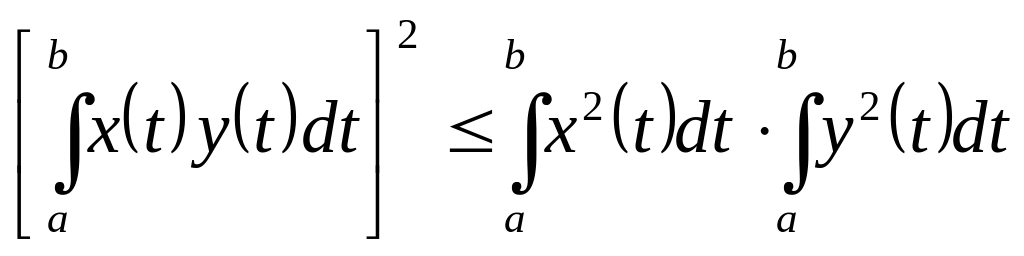неравенство треугольника:
.
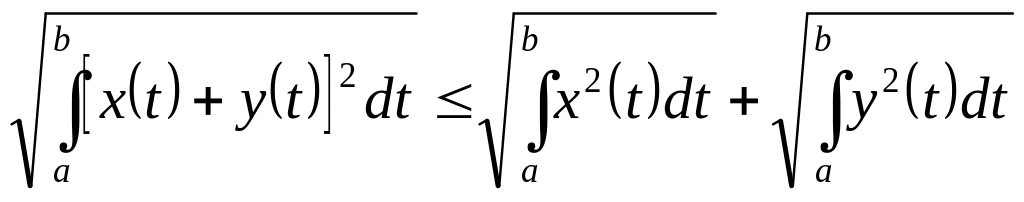3)
-мерное
евклидово пространство
со скалярным произведением по формуле
(4.1.2): норма
;
неравенство Коши – Буняковского:
;
неравенство треугольника:
.
4)
-мерное
евклидово пространство
со скалярным произведением по формуле
(4.1.5): норма:
;
неравенство Коши – Буняковского:
;
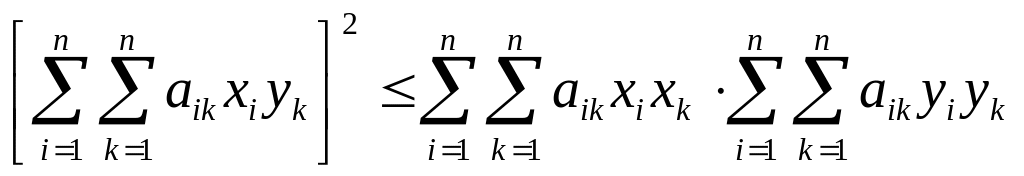неравенство треугольника:
.