§ 4. Теорема о базисном миноре.

1. Понятие линейной зависимости строк. Выше говорилось о том, что строка является линейной комбинацией строк , , …, , если для некоторых вещественных чисел справедливы равенства:

. (1.4.1)

Равенства (1.4.1) (n равенств) можно записать в виде одного матричного равенства:

, (1.4.2)

понимая его в смысле n равенств вида (1.4.1).

Определение 1. Строки матрицы , ,…, называются линейно зависимыми, если существуют такие числа , хотя одно из которых не равно нулю, что справедливы равенства

(1.4.3)

В сокращенном виде:

. (1.4.4)

Определение 2. Строки матрицы , , …, называются линейно независимыми, если равенства (1.4.3) выполняются только в том случае, когда все

/ (1.4.5)

Теорема 1.5. Для того, чтобы строки были линейно зависимы необходимо и достаточно, чтобы одна из этих строк являлась линейной комбинацией остальных строк.

Доказательство. 1) Необходимость. Пусть строки линейно зависимы. Тогда (по определению) справедливо равенство:

. (1.4.6)

при том, что не все равны нулю. Пусть для определенности . Тогда имеем:

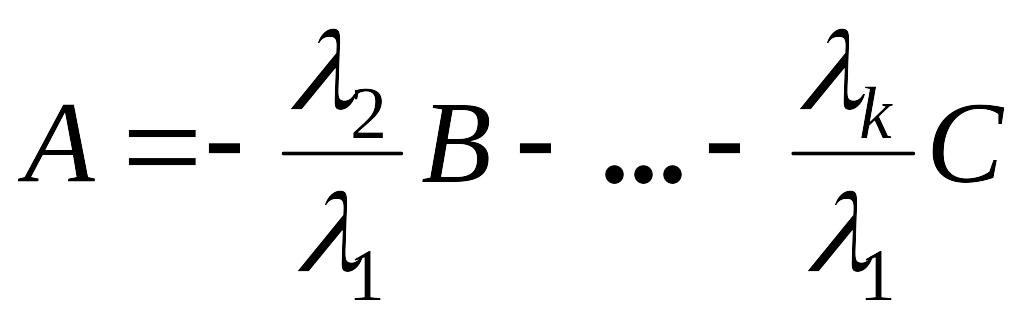(1.4.7)

. Откуда получаем:

, (1.4.8)

т.е. является линейной комбинацией строк

2) Достаточность. Пусть является линейной комбинацией строк Тогда можно записать:

(1.4.9)

или

. (1.4.10)

Выполняется равенство (1.4.10.) при том, что по крайней мере, один из коэффициентов линейной комбинации не равен нулю. Тогда, по определению, строки линейно зависимы. Теорема доказана.

Все приводимые выше рассуждения справедливы не только для строк матрицы, но и для её столбцов.

2. Теорема о базисном миноре. Рассмотрим произвольную (не обязательно квадратную матрицу) :

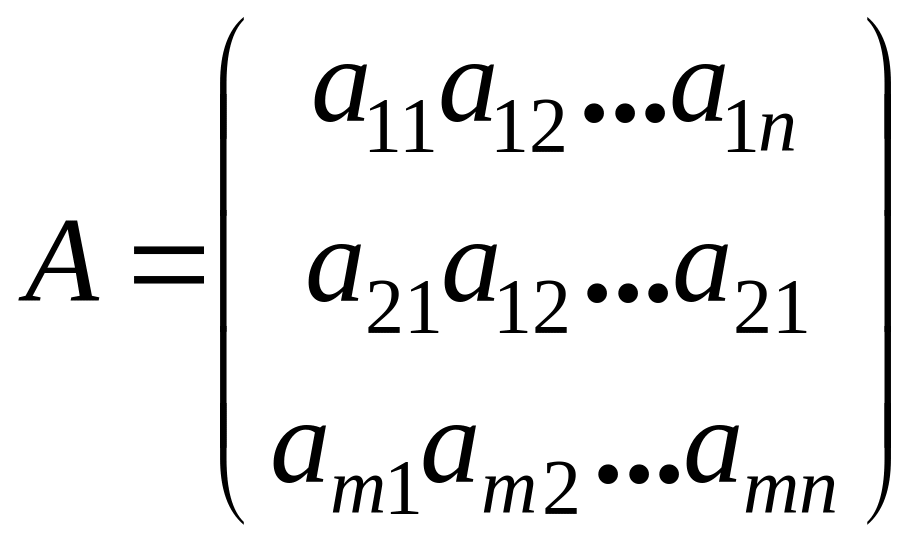. (1.4.11)

Минором -го порядка матрицы будем называть определитель -го порядка с элементами, стоящими на пересечении любых строк и столбцов матрицы .

Если хотя бы один из элементов матрицы отличен от нуля. Тогда найдется целое положительное число , что будут выполняться следующие два условия: у матрицы имеется минор -го порядка, отличный от нуля; всякий минор -го и более высокого порядка (если такой существует) равен нулю.

Определение 3. Минор матрицы максимального порядка , отличный от нуля, называется базисным минором матрицы.

Определение 4. Максимальный порядок отличного от нуля минора матрицы называется рангом матрицы.

Столбцы и строки, на пересечении которых стоит базисный минор матрицы, называют­ся базисными строками и базисными столбцами. У матрицы порядка , где существует несколько миноров -го порядка, отличных от нуля, т.е. базисных миноров.

Теорема 1.6 (о базисном миноре). Базисные строки (базисные столбцы) линейно независимы. Любая строка (любой столбец) матрицы _{является линейной комбинацией базисных строк (базисных столбцов).}

Доказательство. Рассуждения проводим для строк. Если бы базисные строки были линейно зависимыми, то определитель -го был бы равен нулю. Действительно, в случае линейной зависимости базисных строк, одна из них являлась бы линейной комбинацией всех остальных. Но, если из этой строки вычесть линейную комбинацию других строк, величина определителя не изменится. В тоже время появится строка, состоящая из одних нулей, т.е. определитель порядка -базисный минор равен нулю, что противоречит его определению.

Докажем, что любая строка является линейной комбинацией базисных строк матрицы. Не ограничивая общности, будем считать, что базисный минор находится в левом верхнем углу матрицы. Пусть . Убедимся, что -го порядка равен нулю.

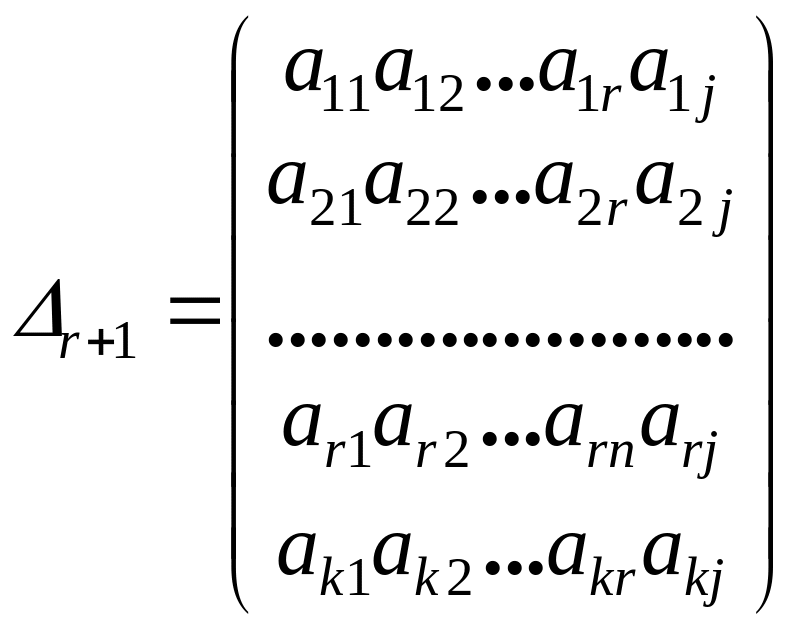. (1.4.12)

Если или , то определитель (1.4.12.) равен нулю в силу того, что он имеет две одинаковые строки или столбца. Если и , то определитель (1.4.12.) является минором матрицы порядка, а всякий такой минор равен нулю по определению базисного минора. Таким образом: при .

Разложим определитель (1.4.12) по последнему столбцу:

(1.4.13)

Алгебраические дополнения элементов последнего столбца не зависят от номера . Поэтому введем обозначение:

. (1.4.14)

Учитывая (1.4.14.), формулу (1.4.13) перепишем в виде:

. (1.4.15)

Соотношение (1.4.15) справедливо для всех . Перепишем (1.4.15) в виде:

. (1.4.16)

.

Окончательно получаем:

. (1.4.17)

Соотношение (1.4.17) показывает, что любая -ая строка матрицы является линейной комбинацией базисных строк. Теорема доказана.