§ 2. Различные методы решения систем линейных уравнений.

Рассмотрим в этом параграфе только квадратные системы линейных уравнений, у которых число неизвестных равно числу уравнений.

1. Метод Крамера. Рассмотрим квадратную систему линейных уравнений:

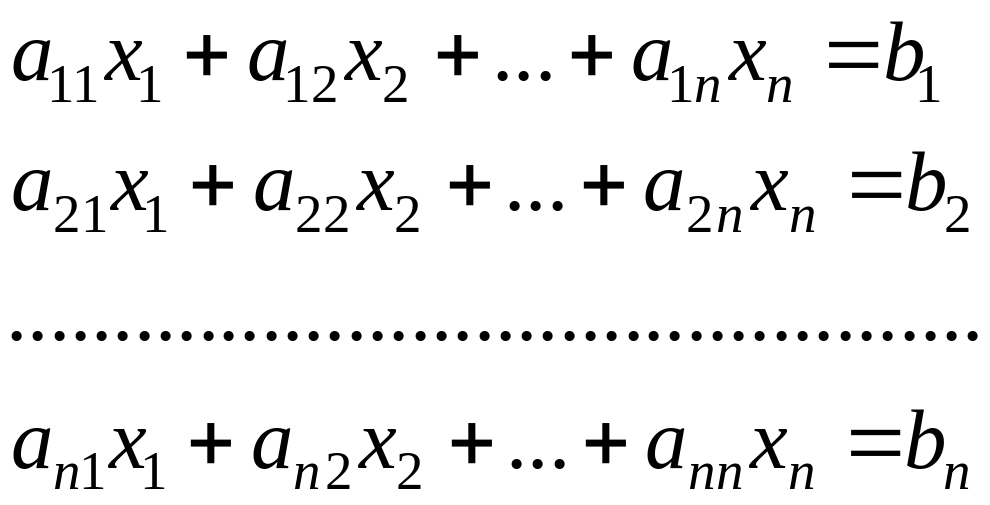(3.2.1)

С отличным от нуля определителем основной матрицы этой системы:

. (3.2.2)

Рассмотрим далее определители , в которых -й столбец заменен столбцом свободных членов:

. (3.2.3)

Тогда, если , то система уравнений (3.2.1) имеет единственное решение, которое определяется формулами Крамера:

. (3.2.4)

2. Матричный метод решения систем линейных уравнений. Если рассмотреть матрицу , являющуюся основной матрицей системы уравнений (3.2.1):

, (3.2.5)

а также матрицы – столбцы неизвестных и свободных членов , то систему уравнений (3.2.1) можно записать в матричном виде:

. (3.2.6)

Для того, чтобы найти неизвестный столбец , требуется умножить матричное уравнение (3.2.6) слева на матрицу , обратную к матрице . В результате получим:

. (3.2.7)

Так как , где - единичная матрица, то окончательно имеем:

. (3.2.8)

Матричное выражение (3.2.8) и представляет собой решение системы уравнений (3.2.1) или матричного уравнения (3.2.6). Таким образом, для получения решения системы уравнений, записанной в матричной форме (3.2.6), требуется предварительно вычислить обратную матрицу по отношению к основной матрице системы (3.2.1). Можно показать, что формула (3.2.8) эквивалентна формулам Крамера (3.2.4).

3. Метод Гаусса. Рассмотрим снова систему линейных уравнений (3.2.1). Пусть ранг основной матрицы системы равен числу уравнений .

Определение 1. Преобразования системы линейных уравнений (3.2.1) называются эквивалентными, если они не меняют ранга ее основной матрицы.

К числу эквивалентных преобразований системы линейных уравнений (3.2.1) относятся:

1). Перестановка строк или столбцов системы уравнений местами.

2). Умножение любого из уравнений системы на постоянное число, отличное от нуля.

3). Прибавление к некоторому уравнению системы любого другого уравнения, умноженного на произвольное постоянное число.

4). Прибавление к некоторому уравнению системы произвольной линейной комбинации других уравнений этой же системы.

Рассмотрим метод решения системы линейных уравнений (3.2.1), основанный на использовании эквивалентных преобразований (метод Гаусса). Метод Гаусса заключается в последовательном исключении неизвестных, начиная с первого, из системы уравнений. Вся схема решения разделяется на два этапа: прямой и обратный ход метода Гаусса. Каждый этап состоит из конечного числа шагов.

Прямой ход метода Гаусса. В дальнейшем на каждом шаге первый элемент (для прямого хода) и последний элемент (для обратного хода) соответствующей строки будем называть ведущим элементом. Если на каждом шаге прямого и обратного хода метода Гаусса ведущий элемент отличен от нуля, то алгоритм метода Гаусса называют простым (собственно метод Гаусса). Если при выполнении прямого или обратного хода метода Гаусса встречаются строки, в которых ведущий элемент обращается в нуль, то требуется перестановка уравнений системы (3.2.1) с тем чтобы добиться выполнения условия отличия от нуля ведущего элемента. Такой алгоритм называют методом Гаусса с выбором ведущего элемента (метод Жордана-Гаусса).

Пусть для определенности коэффициент . Если это не так, то уравнения системы можно перенумеровать таким образом, чтобы выполнялось условие (эквивалентное преобразование 1). Запишем вновь систему уравнений (3.2.1):

. (3.2.9)

Опишем подробно алгоритм выполнения прямого хода метода Гаусса. Так как по условию , то первый шаг прямого хода метода Гаусса заключается в следующем. Умножим первое из уравнений системы (3.2.9) на и сложим со вторым, умножим первое из уравнений системы на и сложим с третьим и т.д., умножим первое из уравнений системы на и сложим с n-м. Переписывая первое уравнение системы (3.2.9) без изменений, а остальные с учетом описанных операций, получим:

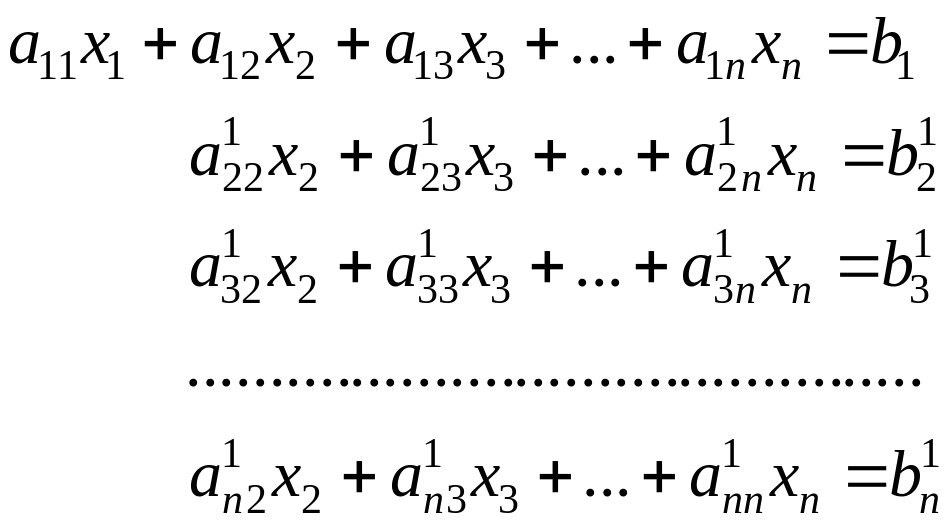, (3.2.10)

где . На этом завершается первый шаг прямого хода метода Гаусса.

На втором шаге прямого хода будем рассматривать все уравнения системы (3.2.10), кроме первого. Перенумеруем оставшиеся уравнения системы таким образом, чтобы выполнялось условие: . Оставляя без изменения первое и второе уравнения системы (3.2.10), остальные уравнения запишем следующим образом: умножая второе уравнение на и складывая с третьим, и т.д. умножая второе уравнение на и складывая с n-м, получим:

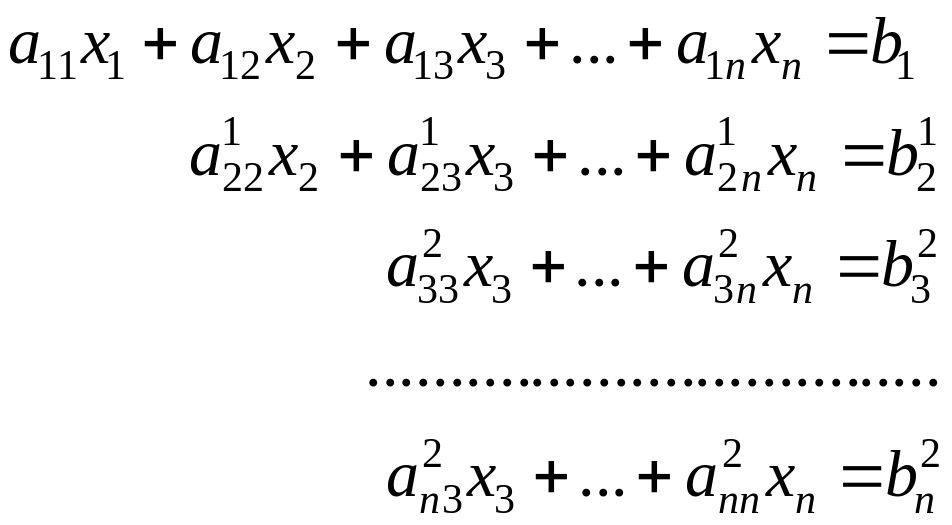, (3.2.11)

где введены обозначения: . На этом завершается второй шаг прямого хода метода Гаусса.

Повторяя описанный процесс исключения неизвестных, после конечного числа шагов, на -м шаге получим систему уравнений с треугольной основной матрицей:

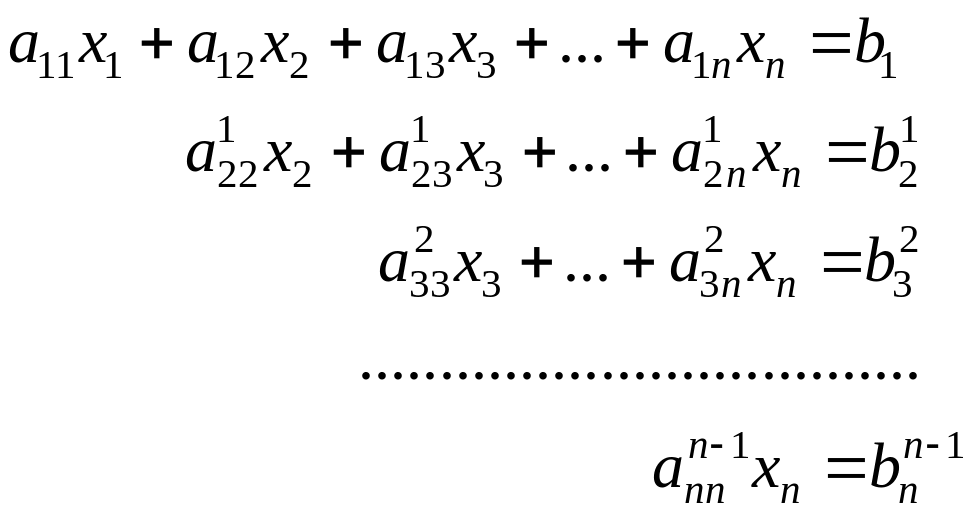. (3.2.12)

Величины и могут быть вычислены аналогично коэффициентам в системах (3.2.10-11) и будут зависеть от коэффициентов всех предыдущих приближений. На этом заканчивается прямой ход метода Гаусса.

Обратный ход метода Гаусса заключается в последовательном исключении неизвестных в обратном порядке, начиная с . Это достигается путем эквивалентных преобразований, аналогичных описанным в прямом ходе, но обращающих в нуль все недиагональные элементы , лежащие выше главной диагонали. В результате получится система уравнений с преобразованной основной матрицей, которая является диагональной. Причем на главной диагонали после деления на соответствующие коэффициенты, стоящие перед неизвестными, будет располагаться вектор решения данной системы . Проиллюстрируем ход решения системы уравнений на следующем примере:

.