§ 2. Матричная запись линейных операторов.

1. Матрицы линейных операторов в заданном базисе линейного пространства . Фиксируем в линейном пространстве базис

. (5.2.1)

Пусть - произвольный элемент пространства . Тогда:

- (5.2.2)

разложение элемента в базисе (5.2.1). Пусть, далее - линейный оператор из . Тогда имеем:

. (5.2.3)

Пусть оператор действует на базисные элементы по следующему правилу:

(5.2.4)

или в развернутом виде:

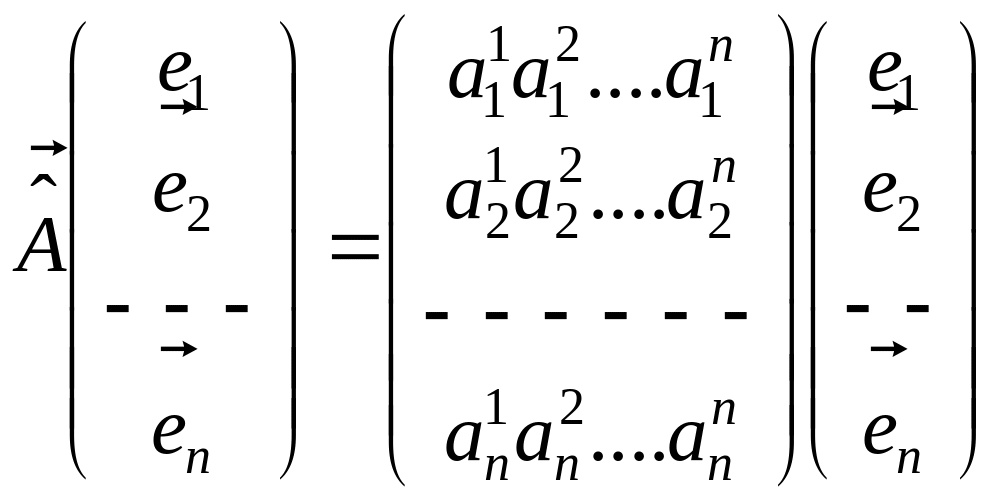(5.2.4’)

Подставляя выражение (5.2.4) в (5.2.3), получим:

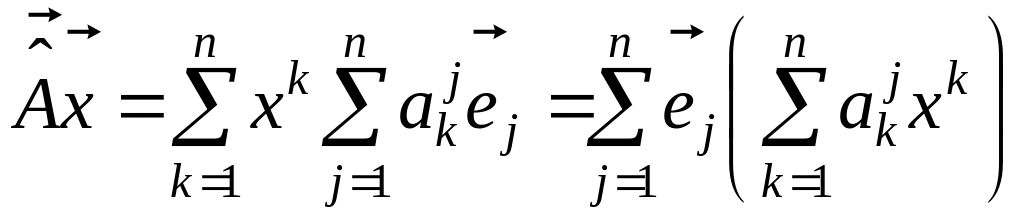. (5.2.5)

Таким образом, если элемент имеет координаты: и справедливо равенство:

, (5.2.6)

то координаты элементов и связаны соотношениями:

(5.2.7)

Квадратная матрица

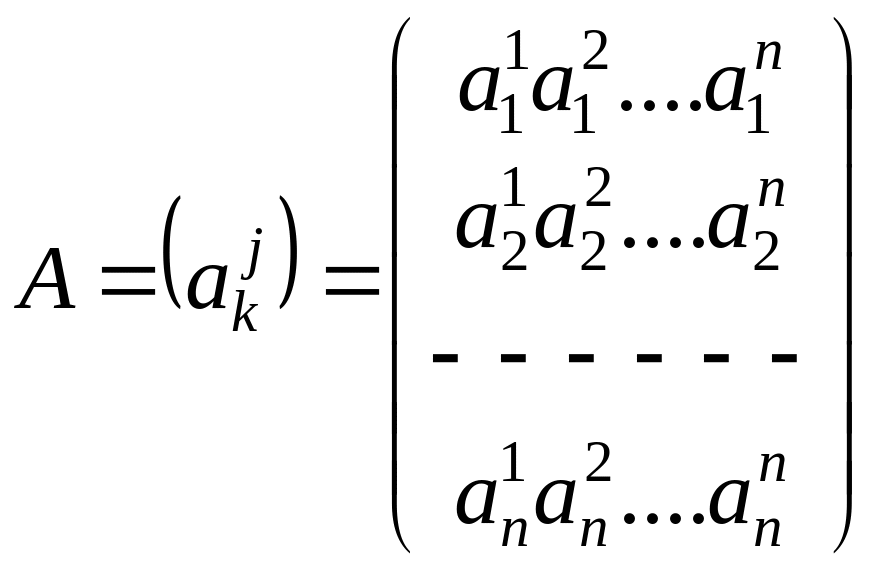(5.2.8)

называется матрицей линейного параметра в заданном базисе (5.2.1).

Замечание 1. Если оператор - нулевой, т.е. , то - нулевая матрица.

Замечание 2. Если оператор - единичный, то - соответствующая ему матрица также является единичной.

Таким образом, установлено, что каждому линейному оператору из в заданном базисе линейного пространства соответствует матрица этого оператора.

Справедливо и обратное утверждение

Терема 5.5. Пусть в линейном пространстве задан базис и пусть - произвольная квадратная матрица, содержащая строк и столбцов. Существует единственный линейный оператор , матрицей которого в заданном базисе является матрица .

Замечание 3. Пусть и - квадратные матрицы порядка , и - соответствующие им линейные операторы в базисе (5.2.1) пространства . Тогда матрице соответствует оператор , где .

Теорема 5.6. Ранг линейного оператора равен рангу матрицы этого оператора: .

Следствие 1.

.

Следствие 2. Обратный оператор для оператора существует только тогда, когда ранг матрицы равен . В этом случае существует и матрица , обратная к .

2. Преобразование матрицы линейного оператора при переходе к новому базису. Пусть - линейное пространство, - линейный оператор из , и - два базиса в . Формулы перехода от базиса к базису имеют вид:

. (5.2.9)

Матрица перехода:

(5.2.10)

Заметим, что . Пусть

и - (5.2.11)

матрицы оператора в базисах (I) и (II). Справедливо следующее утверждение:

Теорема 5.7. Матрицы и оператора в базисах и связаны соотношением:

, (5.2.12)

где - матрица, обратная из (5.2.10).

Доказательство. Если матрицы оператора в базисах и имеют вид (5.2.11), то:

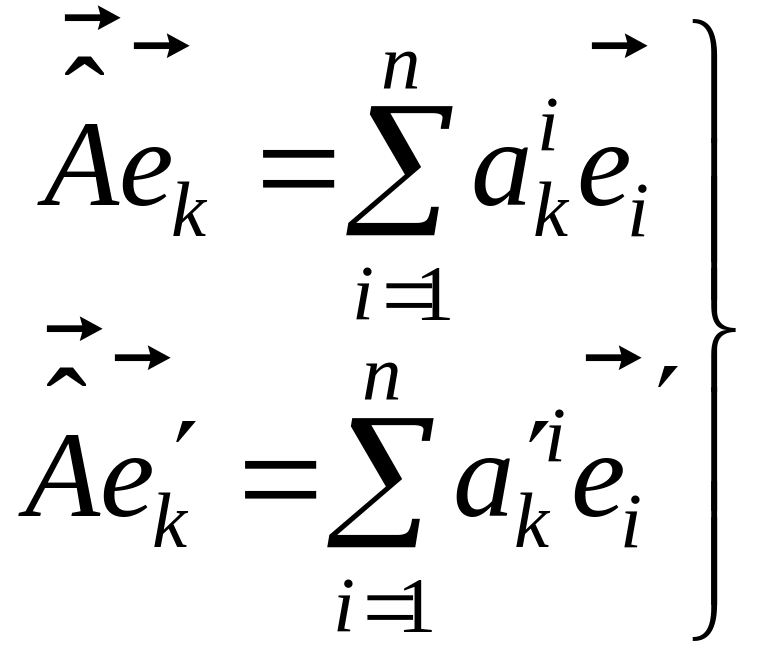(5.2.13)

Так как согласно (5.2.9) : , то из (5.2.13) следует:

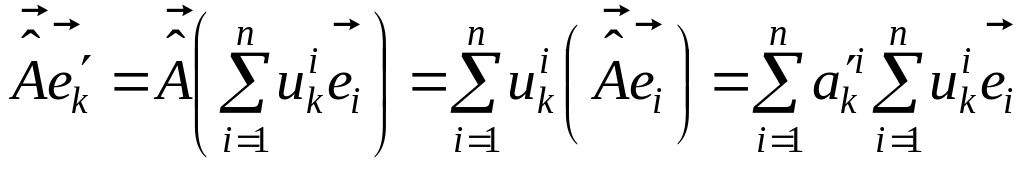. (5.2.14)

Откуда следует, что

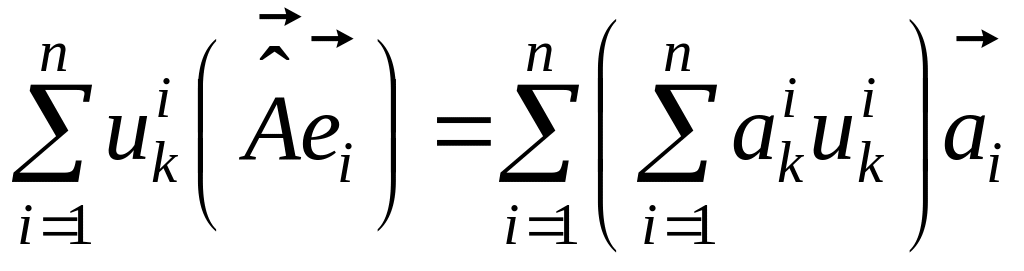. (5.2.15)

Подставляя (5.2.13) в левую часть (5.2.15), получим:

или

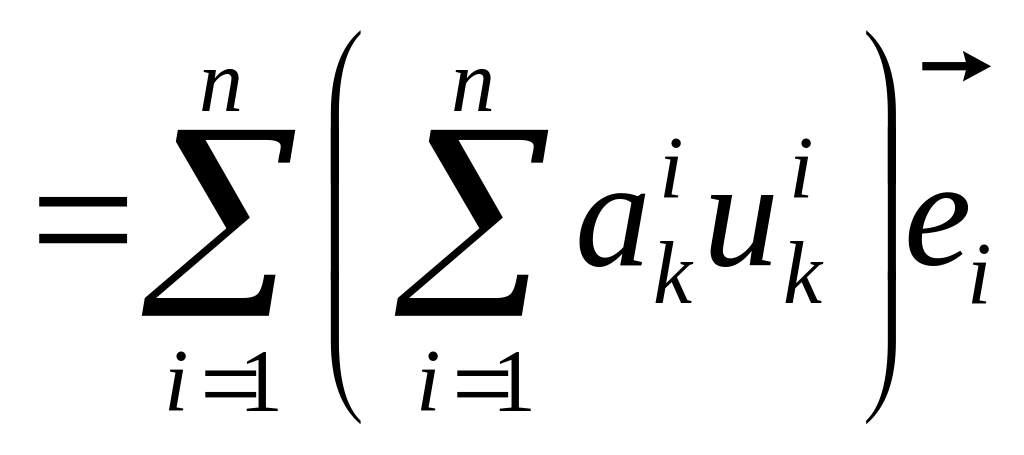. (5.2.16)

Поскольку разложение любого элемента в заданном базисе единственно, то имеют место равенства:

. (5.2.17)

или

, . (5.2.18)

Равенство (5.2.18) эквивалентно матричному равенству:

. (5.2.19)

Умножая (5.2.19) на слева, получим окончательно:

. (5.2.12)

Теорема доказана.

Замечание 1. Преобразование, обратное по отношению к (5.2.12) дается формулой:

. (5.2.20)

Замечание 2. Матрица оператора в базисе имеет вид: . Действительно: и . Если , то и . Поэтому в базисе имеет вид: .

Следствие. Определитель матрицы , соответствующей оператору не зависит от выбора базиса:

. (5.2.21)

В самом деле:

,

так как .

3. Характеристический многочлен линейного оператора. Пусть - линейный оператор, а - единичный оператор из - вещественное комплексное число.

Определение. Характеристическим многочленом оператора называется определитель:

. (5.2.22)

Если - матрица оператора в базисе то

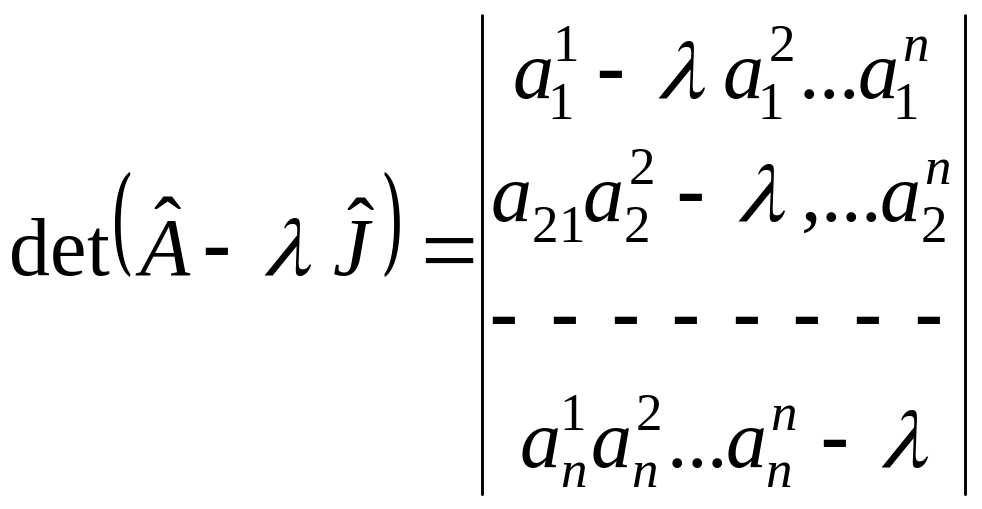(5.2.22’)

Замечание 1. Если (22’) представить в виде:

, (5.2.23)

то так как не зависит от выбора базиса, коэффициенты также не зависят от выбора базиса. Коэффициенты называются инвариантами характеристического многочлена. В частности величина:

. (5.2.24)

также является инвариантом характеристического многочлена (22) и называется следом оператора .

Замечание 2. Уравнение:

(5.2.25)

называется характеристическим уравнением оператора .