§ 4. Закон инерции квадратичных форм.

Классификация квадратичных форм.

1. Закон инерции квадратичных форм. Ранг квадратичной формы равен числу отличных от нуля канонических коэффициентов. Таким образом, число отличных от нуля канонических коэффициентов не зависит от выбора невырожденного преобразования, с помощью которого форма приводится к каноническому виду. Более того, при любом способе приведения формы к каноническому виду не меняется число положительных и отрицательных канонических коэффициентов. Это свойство называется законом инерции квадратичных форм.

Пусть форма в базисе определяется матрицей :

, (6.4.1)

где - координаты вектора в базисе . Допустим, что эта форма при помощи невырожденного преобразования приводится к каноническому виду:

, (6.4.2)

причем - отличные от нуля канонические коэффициенты, занумерованные так, что первые из этих коэффициентов положительные, а следующие коэффициенты отрицательные:

. (6.4.3)

Рассмотрим следующее невырожденное преобразование координат:

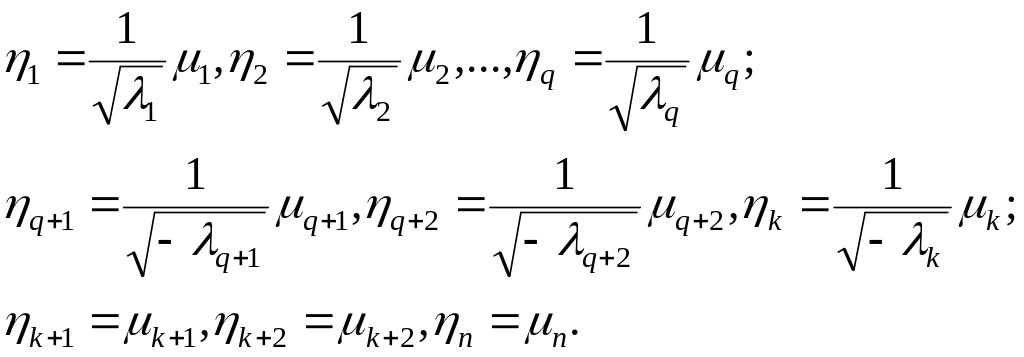(6.4.4)

В результате этого преобразования форма преобразуется к виду:

, (6.4.5)

который называется нормальным видом квадратичной формы .

Итак, с помощью невырожденного преобразования координат вектора в базисе :

(6.4.6)

квадратичная форма (6.4.1) может быть приведена к нормальному виду (6.4.5). При этом преобразование (6.4.6) представляет собой произведение преобразований координат в координаты и координат в координаты по формулам (6.4.4).

Справедливо следующее основное утверждение:

Теорема 6.6 (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами в нормальном виде квадратичной формы не зависит от способа приведения формы к нормальному виду.

Доказательство. Пусть форма с помощью невырожденного преобразования координат (6.4.4) приводится к нормальному виду (6.4.5), а с помощью другого невырожденного преобразования координат приводится к нормальному виду:

. (6.4.7)

Для доказательства теоремы достаточно убедиться в справедливости равенства для индексов из равенств (6.4.7) и (6.4.5).

Предположим противное: . Рассмотрим вначале случай . Случай рассматривается аналогично. Итак, пусть . Покажем, что в этом случае имеется ненулевой вектор такой, что по отношению к базисам, в которых форма имеет вид (6.4.5) и (6.4.7) координаты и этого вектора равны нулю:

; . (6.4.8)

Так как координаты получены путем невырожденного преобразования координат , а координаты - путем аналогичного невырожденного преобразования тех же координат , то соотношения (6.4.8) можно рассматривать как систему линейных однородных уравнений относительно координат искомого вектора в базисе . В развернутом виде система уравнений (6.4.8) с учетом (6.4.6) запишется следующим образом:

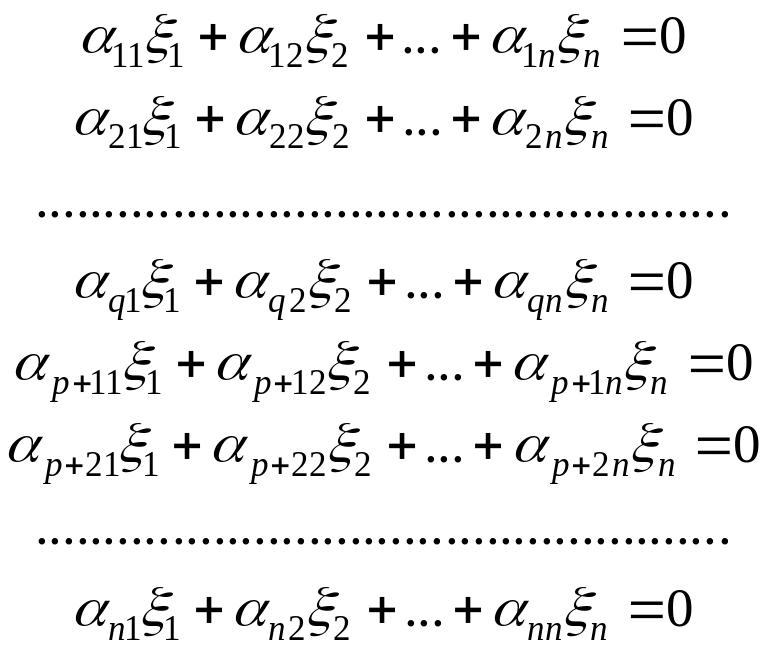(6.4.9)

Так как по предположению , то число уравнений в системе (6.4.9) меньше . Тогда, согласно теореме 2.1, эта система уравнений имеет нетривиальное решение относительно координат искомого вектора . Следовательно, при существует ненулевой вектор , для которого выполняются соотношения (6.4.8).

Вычислим значение квадратичной формы для этого вектора. Согласно соотношениям (6.4.5) и (6.4.7) имеем:

(6.4.10)

Но, так как имеют месть равенства (6.4.8), то должно выполняться условие:

. (6.4.11)

Согласно (6.4.11) является с одной стороны отрицательно определенной квадратичной формой (первое равенство), с другой стороны – положительно определенной квадратичной формой (второе равенство). Соотношение (6.4.11) может быть справедливым тогда и только тогда, когда выполнены условия:

(6.4.12)

Таким образом, в некотором базисе все координаты ненулевого вектора равны нулю (соотношения (6.4.8) и (6.4.12)), т.е. сам вектор равен нулю. Следовательно, предположение приводит к противоречию. К аналогичному противоречию приводит и предположение . Теорема доказана.

2. Классификация квадратичных форм. Введем следующие понятия:

1). Индексом инерции квадратичной формы будем называть число отличных от нуля канонических коэффициентов этой формы (т.е. ее ранг).

2). Положительным индексом инерции квадратичной формы называется число ее положительных канонических коэффициентов.

3). Отрицательным индексом инерции квадратичной формы называется число ее отрицательных канонических коэффициентов.

Сумма положительного и отрицательного индексов инерции равна индексу инерции квадратичной формы: .

В предыдущем пункте было показано, что в любом каноническом базисе квадратичная форма может быть приведена к нормальному виду:

, (6.4.13)

где - координаты вектора в базисе .

2.1. Необходимое и достаточное условие знакоопределенности квадратичной формы. Справедливо утверждение:

Для того, чтобы квадратичная форма , заданная в мерном линейном пространстве , являлась знакоопределенной, необходимо и достаточно, чтобы либо положительный индекс инерции , либо отрицательный индекс инерции был равен размерности пространства . При этом, если , то форма положительно определенная, если , то форма отрицательно определенная.

Доказательство. Ввиду полной аналогии рассмотрения положительно и отрицательно определенных квадратичных форм, проведем доказательство для положительно определенной формы.

1). Необходимость. Так как форма положительно определенная, то (6.4.13) примет вид:

. (6.4.14)

При этом из последнего выражения следует, что при существует ненулевой элемент (вектор) , координаты которого удовлетворяют условиям:

, (6.4.15)

и для которого квадратичная форма . Это противоречит определению положительно определенной квадратичной формы. Поэтому . Необходимость доказана.

2). Достаточность. Пусть . Тогда выражение (6.4.13) примет вид:

. (6.4.16)

Из (6.4.16) следует, что , причем лишь при условии: . Т.е. , если вектор - нулевой. Следовательно - положительно определенная квадратичная форма. Утверждение доказано.

Замечание. Для выяснения вопроса о знакоопределенности квадратичной формы с помощью указанного признака, ее следует привести к каноническому виду.

2.2. Необходимое и достаточное условие знакопеременности квадратичной формы. Справедливо утверждение:

Для того чтобы квадратичная форма была знакопеременной, необходимо и достаточно, чтобы как положительный, так и отрицательный индексы инерции этой формы были отличны от нуля.

Доказательство. 1). Необходимость. Пусть - знакопеременная квадратичная форма. Она принимает как положительные, так и отрицательные значения. Следовательно, форма (6.4.13) содержит как положительные, так и отрицательные слагаемые. Следовательно положительный индекс инерции и отрицательный индекс инерции .

2). Достаточность. Пусть и . Тогда для вектора у которого форма , а для вектора , у которого , а , квадратичная форма . Следовательно, в силу определения, форма знакопеременна. Утверждение доказано.

2.3. Необходимое и достаточное условие квазизнакоопределенности квадратичной формы. Справедливо утверждение: Для того, чтобы квадратичная форма была квазизнакоопределенной, необходимо и достаточно, чтобы выполнялись соотношения: либо и , либо и .

Доказательство. Рассмотрим случай положительно квазизнакоопределенной квадратичной формы. Случай отрицательно квазизнакоопределенной квадратичной формы рассматривается аналогично.

1). Необходимость. Пусть форма положительно квазизнакоопределенная. Тогда очевидно, что и . Если бы выполнялось условие , то форма была бы положительно определенной.

2). Достаточность. Если и , то , и для ненулевого вектора с координатами имеем , т.е. - положительно квазизнакоопределенная квадратичная форма.

3. Критерий Сильвестра знакоопределенности квадратичной формы. Пусть форма в базисе определяется матрицей :

. (6.4.17)

Пусть далее:

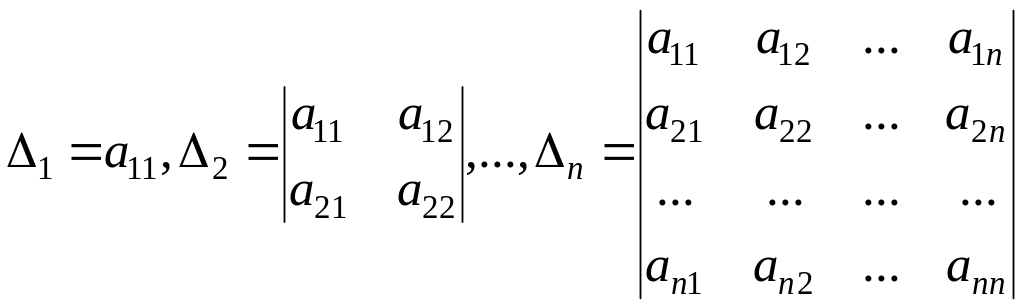- (6.4.18)

угловые миноры и определитель матрицы . Тогда справедливо утверждение:

Теорема 6.7 (критерий Сильвестра). Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы выполнялись следующие неравенства:

. (6.4.19)

Для того чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы знаки угловых миноров чередовались, причем

. (6.4.20)

Доказательство. 1). Необходимость. Пусть квадратичная форма является знакоопределенной. Докажем вначале, что из знакоопределенности квадратичной формы следует, что .

Предположим противное. Пусть некоторый . Тогда существует ненулевой элемент такой, что . Рассмотрим следующую однородную систему линейных уравнений:

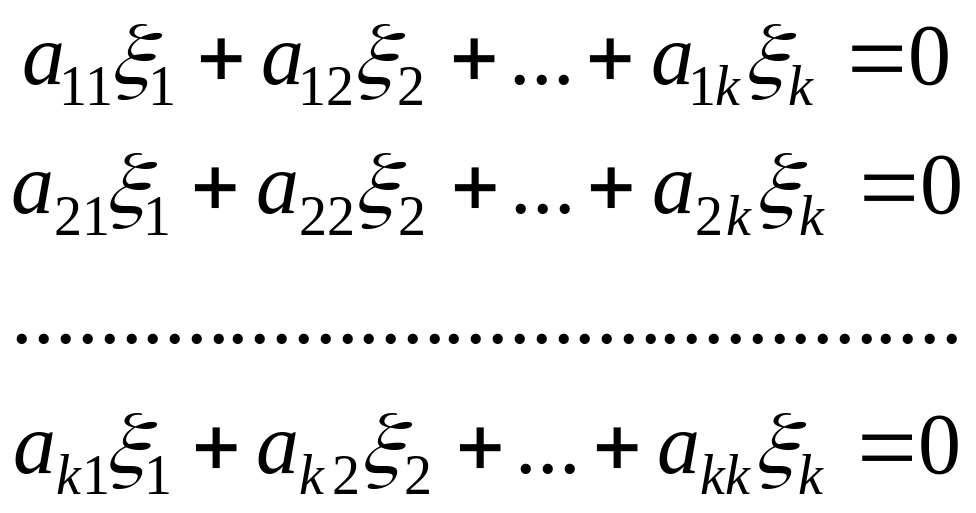(6.4.21)

Так как - определитель этой системы и , то существует нетривиальное решение системы (6.4.21), т.е. не все . Умножим первое из уравнений системы на , второе на , …, е на и, просуммировав результат, получим:

. (6.4.22)

Левая часть выражения (6.4.22) представляет собой квадратичную форму для ненулевого элемента . Так как и , согласно (6.4.22), то это противоречит предположению о знакоопределенности квадратичной формы . Поэтому .

Докажем теперь, что из условия положительной (отрицательной) определенности квадратичной формы необходимо следуют условия (6.4.19) (условия (6.4.20)). Так как все , то квадратичную форму можно привести к каноническому виду. Используя метод Якоби, получим канонические коэффициенты квадратичной формы в следующем виде (§3):

. (6.4.23)

Так как для положительно определенной квадратичной формы

, (6.4.24)

то все и, следовательно, выполняются условия (6.4.19). Для отрицательно определенной формы:

, (6.4.25)

но тогда, в соответствии с (6.4.23): , и , и , …, , , т.е. выполняется условие (6.4.20) и знаки угловых миноров чередуются. Необходимость доказана.

2). Достаточность. Пусть выполняются условия, наложенные на угловые миноры в формулировке теоремы. Так как все , то форму можно привести к каноническому виду методом Якоби. При этом канонические коэффициенты могут быть вычислены по формулам (6.4.23). Если , то из соотношений (6.4.23) следует, что все и форма положительно определенная. Если же знаки угловых миноров чередуются , то из формул (6.4.23) следует, что все и форма является отрицательно определенной. Теорема доказана.