§ 2. Квадратичные формы.

1. Понятие квадратичной формы. Пусть - симметричная билинейная форма, заданная на линейном пространстве .

Определение 1. Квадратичной формой называется числовая функция одного векторного аргумента , которая получается из билинейной формы , при .

Симметричная билинейная форма называется полярной к квадратичной форме .

Полярная билинейная форма и квадратичная форма связаны следующим соотношением:

. (6.2.1)

Действительно вычислим величину :

. (6.2.2)

Так как билинейная форма симметрична, то

. (6.2.3)

Поэтому:

. (6.2.4)

Откуда непосредственно следует:

. (6.2.1)

Пусть в конечномерном линейном пространстве , задана симметричная билинейная форма , полярная к квадратичной форме. Пусть, кроме того, в задан базис .

Согласно теореме 6.2. форму можно представить в виде:

, (6.2.5)

где и - координаты векторов и в базисе . Поэтому в силу (6.2.3), имеем:

. (6.2.6)

Полагая (или, что то же самое, ), получим следующее представление для квадратичной формы:

. (6.2.7)

Матрица называется матрицей квадратичной формы в заданном базисе . Согласно (6.2.6), матрица является симметричной. Матрица квадратичной формы при переходе к новому базису преобразуется по формуле (6.1.13):

. (6.2.8)

Ранг матрицы не меняется при переходе к новому базису. Ранг матрицы квадратичной формы называется рангом квадратичной формы. Если ранг квадратичной формы равен размерности пространства , то форма называется невырожденной, в противном случае – вырожденной.

2. Виды квадратичных форм.

Определение 1. Квадратичная форма называется:

1) положительно (отрицательно) определенной, если для любого ненулевого выполняется неравенство:

; . (6.2.9)

Такие формы называются также знакоопределенными.

2) знакопеременной, если существуют также элементы , что

; . (6.2.10)

3) квазизнакоопределенной, если для всех справедливы неравенства:

или , (6.2.11)

но имеется хотя бы один ненулевой элемент , для которого

. (6.2.12)

Справедливо утверждение: Если представляет собой билинейную форму, полярную к квадратичной форме , то удовлетворяет всем аксиомам скалярного произведения векторов в евклидовом пространстве.

Рассмотрим аксиомы скалярного произведения. Если для скалярного произведения элементов и вместо обозначения использовать символ , то аксиомы запишутся в виде:

1). .

2). .

3). .

4). , и , если .

Таким образом, выполняются все аксиомы скалярного произведения.

Замечание. Аксиомы скалярного произведения можно рассматривать как совокупность требований, определяющих билинейную форму, полярную к положительно определенной квадратичной форме. Поэтому скалярное произведение в линейных пространствах может быть задано с помощью такого вида билинейной формы.

§ 3. Приведение квадратичной формы к каноническому виду.

1. Канонический вид квадратичной формы.

Определение 1. Квадратичная форма называется приведенной к каноническому виду, если существует в - мерном линейном пространстве такой базис , что в этом базисе квадратичная форма имеет вид:

. (6.3.1)

Величины - координаты элемента в базисе , - канонические коэффициенты квадратичной формы .

Будем рассматривать квадратичные формы в произвольном вещественном линейном пространстве. Докажем возможность приведения к каноническому виду любой квадратичной формы в произвольном вещественном линейном пространстве. Параллельно рассмотрим основные методы приведения квадратичных форм к каноническому виду.

Все дальнейшие рассуждения основаны на следующем утверждении: каждому преобразованию базиса отвечает невырожденное преобразование координат, а невырожденному преобразованию координат преобразование базиса. Поэтому вопрос о приведении квадратичной формы к каноническому виду можно решить путем выбора соответствующего невырожденного преобразования координат.

2. Метод Лагранжа. Справедливо следующее основное утверждение.

Теорема 12.4. Любая квадратичная форма , заданная в - мерном линейном пространстве , с помощью невырожденного линейного преобразования координат может быть приведена к каноническому виду (6.3.1).

Доказательство. Приведем доказательство теоремы методом Лагранжа. Основная идея этого метода заключается в последовательном дополнении квадратного трехчлена по каждому аргументу до полного квадрата. Будем считать, что . Если , то ее матрица в любом базисе состоит из нулевых элементов, и поэтому такая форма по определению имеет канонический вид в любом базисе. Итак, пусть . Пусть, кроме того, в данном базисе:

. (6.3.2)

Убедимся, что с помощью невырожденного преобразования координат квадратичную форму можно преобразовать так, что коэффициент при квадрате первой координаты вектора будет неравен нулю: . Если в (6.3.2) , то нужное преобразова­ние является тождественным . Всякое тождественное преобразование не вырождено: . Пусть теперь , но какой-либо из коэффициентов , . Тогда, для того, чтобы добиться требуемого результата , необходимо произвести перенумерацию базисных векторов, которая также является невырожденным преобразованием. После соответствующей перенумерации имеем: . Возможен, наконец, третий случай, когда все , . Тогда, по определению квадратичной формы, хотя бы один из коэффициентов , . Пусть . Если это не так, снова произведем перенумерацию базисных векторов так, чтобы . Рассмотрим следующее невырожденное преобразование координат:

. (6.3.3)

Преобразование (6.3.3) не вырождено, так как его определитель . Так как в рассматриваемом случае все , то квадратичная форма (6.3.2) имеет вид:

(6.3.4)

После подстановки преобразование (6.3.3) в (6.3.4), получим:

(6.3.5)

Таким образом, коэффициент , т.е. всегда можно добиться того, чтобы .

Выделим теперь в выражении (6.3.2) группу элементов, содержащих .

. (6.3.6)

Преобразим первую группу слагаемых следующим образом:

(6.3.7)

Подставляя (6.3.7) в (6.3.6) и выполняя тождественные преобразования, получим:

. (6.3.8)

- коэффициенты квадратичной формы, получающиеся после выполнения преобразований.

Рассмотрим теперь невырожденное преобразование:

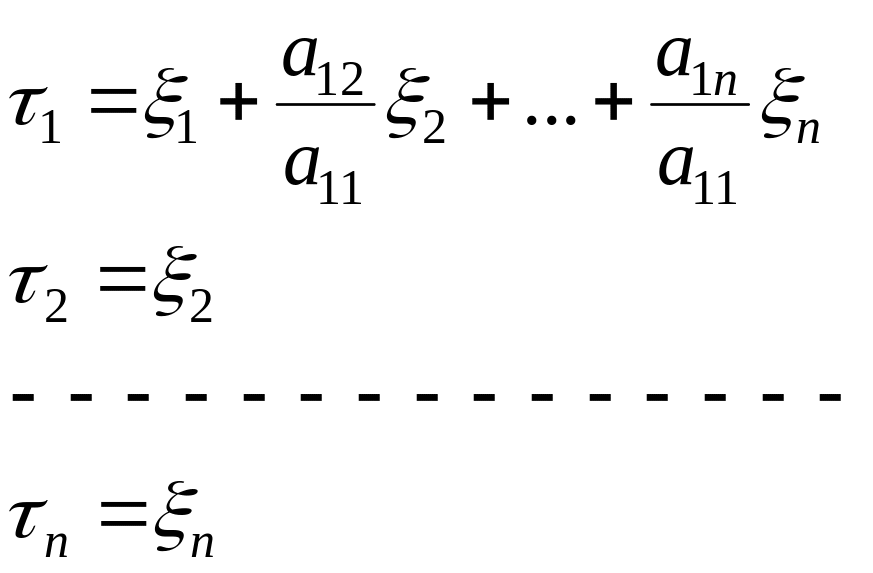(6.3.9)

С помощью этого преобразования квадратичная форма (6.3.8) запишется в виде:

. (6.3.10)

Таким образом, если квадратичная форма (6.3.2), то с помощью преобразования (6.3.9) ее можно привести к виду (6.3.10)

Обратимся теперь к квадратичной форме . Если эта форма тождественно равна нулю, то вопрос о приведении квадратичной формы к каноническому виду решен. Если же форма , то можно повторить описанные выше рассуждения для координат , не меняя при этом координату . Такого типа преобразования координат будут невырожденными. За конечное число шагов путем описанных невырожденных линейных преобразований квадратичная форма из (6.3.2) будет приведена к каноническому виду. Нужное преобразование от исходных координат к конечным может быть получено как результат перемножения найденных в процессе доказательства невырожденных преобразований. Теорема доказана.

Замечание 1. Базис, в котором квадратичная форма имеет канонический вид, называется каноническим. Канонический базис определяется неоднозначно.

Замечание 2. Если форма из (6.3.2) приведена к каноническому виду, то, вообще говоря, не все канонические коэффициенты отличны от нуля. Оставшиеся отличные от нуля канонические коэффициенты и перенумеровывая их, получим:

. (6.3.11)

Ясно, что . Так как по определению, ранг квадратичной формы равен рангу ее матрицы в любом базисе, то из (6.3.11) и условия при , следует, что ранг формы равен .

Таким образом, справедливо утверждение: число отличных от нуля канонических коэффициентов равно рангу квадратичной формы.

3. Метод Якоби. При некоторых дополнительных предположениях о квадратичной форме можно указать явные формы перехода от данного базиса к каноническому базису и формулы для канонических коэффициентов .

Предварительно введем понятие треугольного преобразования базисных векторов. Преобразование базисных векторов называется треугольным, если оно имеет вид:

(6.3.12)

Преобразование (6.3.12) генерируется матрицей:

(6.3.13)

Замечание 3. Определитель матрицы (6.3.13) , поэтому векторы образуют базис.

Введем в рассмотрение угловые миноры матрицы коэффициентов квадратичной формы в базисе , обозначим их символами: .

. (6.3.14)

Справедливо следующее основное утверждение:

Теорема 12.5. Пусть миноры матрицы квадратичной формы в базисе не равны нулю. Тогда существует единственное треугольное преобразование базисных векторов , с помощью которого форму можно привести к каноническому виду.

Доказательство. Коэффициенты квадратичной формы в базисе вычисляются по формулам:

. (6.3.15)

Если форма в базисе имеет канонический вид, то , при . Поэтому для доказательства теоремы достаточно построить с помощью треугольника преобразование (6.3.12) такой базис , в котором будут выполняться соотношения:

; при , или, что то же самое, при . (6.3.16)

При этом, конечно, следует убедиться, что искомое преобразование единственно.

Применяя квадратичную форму к преобразованиям (6.3.12), получим:

(6.3.17)

Для того, чтобы выполнялись условия (6.3.16), достаточно, чтобы выполнялись условия:

. (6.3.18)

Таким образом, существует базис , в котором квадратичная форма имеет канонический вид. Докажем, что этот базис единственен. Для этого распишем (6.3.18) в развернутом виде, учитывая, что

(6.3.19)

получим:

(6.3.20)

(6.3.21)

Введем обозначения:

, (6.3.22)

тогда получим следующую систему уравнений:

(6.3.23)

Система (6.3.23) есть линейная неоднородная система относительно неизвестных коэффициентов . Ее главный определитель . Поэтому система (6.3.23) имеет единственное решение. Следовательно, искомое треугольное преобразование (6.3.12) единственно. Теорема доказана.

Приведем формулы, по которым можно вычислить коэффициенты искомого треуголь­ного преобразования (6.3.12), а также формулы для канонических коэффициентов .

Обозначим символом минор матрицы , стоящий на пересечении строк этой матрицы с номерами и столбцов с номерами: , тогда, согласно формул Крамара, из системы (6.3.23) получим:

. (6.3.24)

Для коэффициентов имеем:

. (6.3.25)

Подставляя (6.3.24) в (6.3.25), окончательно получим:

. (6.3.26)

Так как , поэтому:

. (6.3.27)