
- •Глава I. Матрицы и определители.
- •§ 1. Матрицы.
- •§ 2. Определители второго и третьего порядка.
- •§ 3. Определители n-го порядка.
- •§ 4. Теорема о базисном миноре.
- •3. Необходимое и достаточное условие равенства нулю определителя.
- •Глава II. Линейные пространства.
- •§ 1. Понятие линейного пространства.
- •2. Некоторые свойство произвольных линейных пространств.
- •§2. Базис и размерность линейного пространства.
- •2. Базис и координаты.
- •§ 3. Преобразование координат при преобразовании базиса
- •Глава III. Системы линейных уравнений.
- •§ 3.1. Условие совместности линейной системы.
- •§ 2. Различные методы решения систем линейных уравнений.
- •Глава IV. Евклидовы пространства.
- •§1.Вещественное евклидово пространство и его основные свойства.
- •1. Определение вещественного евклидова пространства.
- •§2. Ортонормированный базис конечномерного евклидова пространства.
- •2. Свойства ортонормированного базиса.
- •§ 3. Комплексное евклидово пространство.
- •2. Примеры конкретных комплексных евклидовых пространств.
- •Глава V Линейные операторы.
- •§ 1. Понятие линейного оператора и его свойства.
- •§ 2. Матричная запись линейных операторов.
- •§ 3. Собственные значения и собственные векторы линейных операторов.
- •2. Основные свойства собственных значений собственных векторов.
- •§ 4. Линейные самосопряженные операторы в евклидовом пространстве.
- •2. Самосопряженные (эрмитовы) операторы.
- •§5. Унитарные и нормальные операторы.
- •1.Понятие унитарного оператора.
- •2. Понятие нормального оператора.
- •3. Основные свойства унитарных и нормальных операторов.
- •§ 6. Канонический вид линейных операторов.
- •Глава VI билинейные и квадратичные формы
- •§ 1. Билинейная форма.
- •§ 2. Квадратичные формы.
- •2. Виды квадратичных форм.
- •§ 3. Приведение квадратичной формы к каноническому виду.
- •1. Канонический вид квадратичной формы.
- •§ 4. Закон инерции квадратичных форм.
§ 3. Преобразование координат при преобразовании базиса
- мерного линейного пространства.
1.Прямое и обратное преобразование
базисов. Пусть
и
![]() - два произвольных базиса
-
мерного линейного пространства
.
Как всякий элемент пространства
,
каждый элемент
может быть разложен по базису
.
Предположим, что элементы базиса
- два произвольных базиса
-
мерного линейного пространства
.
Как всякий элемент пространства
,
каждый элемент
может быть разложен по базису
.
Предположим, что элементы базиса
![]() выражаются через элементы
по формуле:
выражаются через элементы
по формуле:
 (2.3.1.)
(2.3.1.)
Формула (2.3.1.) означает, что переход от первого базиса ко второму задается матрицей:
![]() (2.3.2.)
(2.3.2.)
Определитель матрицы
не равен нулю
![]() ,
ибо, в противном случае, в силу теоремы
1.7 строки матрицы
были бы линейно зависимыми, тогда линейно
зависимыми были бы и элементы
,
ибо, в противном случае, в силу теоремы
1.7 строки матрицы
были бы линейно зависимыми, тогда линейно
зависимыми были бы и элементы
![]() ,
что невозможно, так как они образуют
базис
,
что невозможно, так как они образуют
базис
![]() мерного
пространства.
мерного
пространства.
Докажем, что обратный переход от второго
базиса
к первому
![]() осуществляется с помощью матрицы
,
обратной к
:
осуществляется с помощью матрицы
,
обратной к
:
 . (2.3.3)
. (2.3.3)
Для этого умножим поочередно уравнения
системы (2.3.1) на
![]() .
В результате, получим:
.
В результате, получим:
 . (2.3.4)
. (2.3.4)
Сложив все уравнения системы (2.3.4),
получим (![]() ):
):
 . (2.3.5)
. (2.3.5)
Согласно свойствам определителей, сумма:
![]() . (2.3.6)
. (2.3.6)
Поэтому система уравнений (2.3.5) перепишется в виде:
![]() ,
(2.3.7)
,
(2.3.7)
где
![]() - символ Кронекера. Выражая
- символ Кронекера. Выражая
![]() из (2.3.7), получим формулы обратного
преобразования:
из (2.3.7), получим формулы обратного
преобразования:
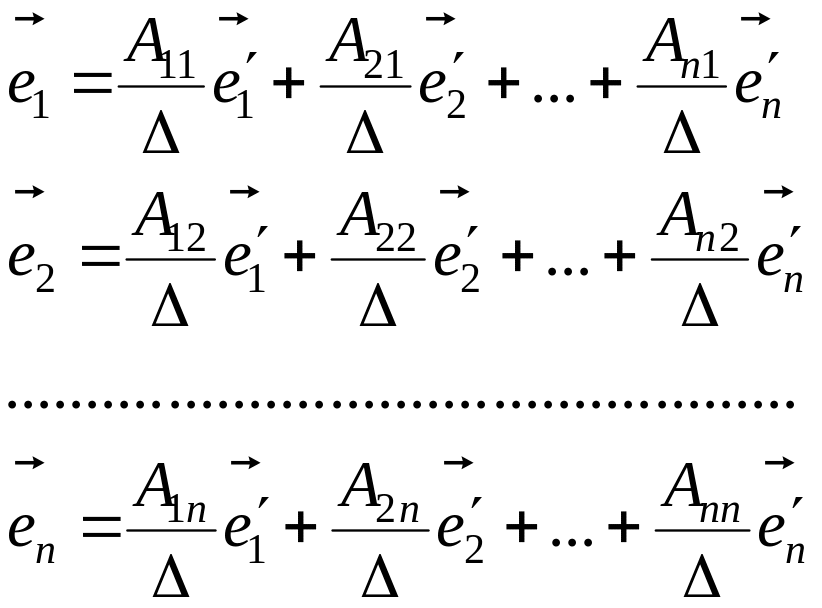 . (2.3.8)
. (2.3.8)
Из (2.3.8) видно, что обратное преобразование от второго базиса к первому генерируется матрицей (2.3.3), обратной к (2.3.2).
2. Связь между преобразованием базисов и преобразованием соответствующих координат. Установим теперь формулы, по которым преобразуются координаты одного и того же элемента линейного пространства .Пусть, как и раньше, базис преобразуется в базис с помощью невырожденной матрицы (2.3.2.). Обратное преобразование задается матрицей (2.3.3.). Пусть, далее - произвольный элемент линейного пространства . В базисе элемент имеет координаты:
![]() . (2.3.8)
. (2.3.8)
В базисе тот же элемент имеет координаты:
![]() . (2.3.9)
. (2.3.9)
Получим формулы преобразования координат элемента (n-мерного вектора) при переходе от одного базиса к другому:
![]() . (2.3.10)
. (2.3.10)
Подставляя в последнее равенство вместо
элементов
![]() их значения из (2.3.7), получим:
их значения из (2.3.7), получим:
 (2.3.11)
(2.3.11)
В силу единственности разложения по базису, из (2.3.11) получим:
 (2.3.12)
(2.3.12)
Откуда, приравнивая коэффициенты при одинаковых векторах слева и справа, получим:
 (2.3.13)
(2.3.13)
Из приведенных рассуждений можно сделать
следующий вывод: если переход от первого
базиса
ко второму
![]() задается невырожденной матрицей A
(2.3.2), то обратный переход задается
обратной матрицей
(2.3.3). Переход же от координат
задается невырожденной матрицей A
(2.3.2), то обратный переход задается
обратной матрицей
(2.3.3). Переход же от координат
![]() произвольного элемента
в первом базисе, к координатам
произвольного элемента
в первом базисе, к координатам
![]() того же элемента во втором базисе
задается матрицей:
того же элемента во втором базисе
задается матрицей:
 , (2.3.14)
, (2.3.14)
транспонированной к обратной матрице , т.е.:
![]() . (2.3.15)
. (2.3.15)
Глава III. Системы линейных уравнений.
§ 3.1. Условие совместности линейной системы.
1. Понятие системы линейных уравнений и ее решения. В общем случае система m линейных уравнений с n неизвестными имеет вид:
 (3.1.1)
(3.1.1)
При этом, через
обозначаются неизвестные величины,
подлежащие определению (их число
равно n). Число неизвестных n не
обязательно равно числу m уравнений
системы. Числа
![]() ,
называются коэффициентами линейной
системы уравнений. Числа
,
называются коэффициентами линейной
системы уравнений. Числа
![]() называются свободными членами линейной
системы. Каждый коэффициент
имеет два индекса, первый из которых i
указывает номер уравнения, а второй –
j указывает номер неизвестного, при
котором стоит этот коэффициент
.
называются свободными членами линейной
системы. Каждый коэффициент
имеет два индекса, первый из которых i
указывает номер уравнения, а второй –
j указывает номер неизвестного, при
котором стоит этот коэффициент
.
Система линейных уравнений (3.1.1) называется однородной, если все ее свободные члены равны нулю:
![]() . (3.1.2)
. (3.1.2)
Система называется неоднородной, если
хотя бы один из
![]() .
Система (3.1.1) называется квадратной,
если число ее уравнений m равно числу
неизвестных n:
.
.
Система (3.1.1) называется квадратной,
если число ее уравнений m равно числу
неизвестных n:
.
Решением системы линейных уравнений
(3.1.1) называется такая совокупность из
n чисел
![]() ,
которая при подстановке в систему
(3.1.1) вместо неизвестных
,
обращает все уравнения системы в
тождества.
,
которая при подстановке в систему
(3.1.1) вместо неизвестных
,
обращает все уравнения системы в
тождества.
Система уравнений (3.1.1) называется
совместной, если она имеет хотя бы одно
решение и несовместной, если у нее не
существует ни одного решения. Совместная
система уравнений может иметь как одно,
так и несколько решений. Два решения
системы уравнений (3.1.1):
![]() и
и
![]() называются различными, если нарушается
хотя бы одно из следующих равенств:
называются различными, если нарушается
хотя бы одно из следующих равенств:
![]() . (3.1.3)
. (3.1.3)
Совместная система линейных уравнений (3.1.1) называется определенной, если она имеет единственное решение и неопределенной, если она имеет по крайней мере два различных решения.
Систему уравнений (3.1.1) удобно записывать в матричной форме. Рассмотрим следующие матрицы: матрицу A:
![]() , (3.1.4)
, (3.1.4)
которую будем называть основной матрицей системы (3.1.1) и матрицу-столбец X, состоящую из неизвестных:
![]() . (3.1.5)
. (3.1.5)
Тогда произведение этих матриц будет равно:
![]() , (3.1.6)
, (3.1.6)
где B – матрица-столбец свободных членов. Таким образом:
![]() . (3.1.6’)
. (3.1.6’)
2. Нетривиальная совместность однородной системы линейных уравнений. Рассмотрим вначале однородную систему линейных уравнений.
 . (3.1.7)
. (3.1.7)
Отметим сразу, что система уравнений
(3.1.7) всегда совместна, поскольку она
всегда имеет так называемое тривиальное
решение:
![]() .
Возникает вопрос о том, при каких условиях
система уравнений (3.1.7) является
нетривиально совместной, т.е. имеет
кроме нулевого и другие решения.
Справедливо утверждение:
.
Возникает вопрос о том, при каких условиях
система уравнений (3.1.7) является
нетривиально совместной, т.е. имеет
кроме нулевого и другие решения.
Справедливо утверждение:
Теорема 3.1. Однородная система линейных уравнений имеет нетривиальное решение тогда и только тогда, когда ранг r матрицы A больше числа ее столбцов n.
Следствие. Однородная квадратная система линейных уравнений имеет нетривиальное решение тогда и только тогда, когда определитель матрицы A (3.1.4), составленный из коэффициентов при неизвестных, равен нулю.
3. Условие совместности общей линейной системы. Установим теперь необходимое и достаточное условие совместности общей линейной системы уравнений. Пусть дана произвольная система уравнений с неизвестными (3.1.1). С этой системой связывают две матрицы: матрицу (3.1.4), называемую основной матрицей системы (3.1.1) и матрицу :
![]() , (3.1.8)
называемую расширенной матрицей системы
уравнений (3.1.1).
, (3.1.8)
называемую расширенной матрицей системы
уравнений (3.1.1).
Справедливо следующее основное утверждение.
Теорема 4.2 (Кронекера – Капелли). Для того, чтобы система линейных уравнений (3.1.1) являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы (3.1.8) этой системы был равен рангу ее основной матрицы (3.1.4).
Доказательство. 1). Необходимость.
Пусть система уравнений (3.1.1) совместна,
т.е. существуют такие числа
![]() ,
что справедливы равенства:
,
что справедливы равенства:
 . (3.1.9)
. (3.1.9)
Обозначим через ранг основной матрицы системы уравнений (3.1.1). Рассмотрим базисных столбцов этой матрицы. В силу теоремы 1.6 (о базисном миноре) всякий столбец матрицы (3.1.4) является линейной комбинацией ее базисных столбцов. Но, в силу равенств (3.1.9) и последний столбец матрицы также линейно выражается через базисные столбцы матрицы , т.е. является их линейной комбинацией. Следовательно, ранг матрицы равен рангу матрицы . Необходимость доказана.
2). Достаточность. Пусть ранги основной и расширенной матриц системы уравнений (3.1.1) совпадают и равны . Тогда базисных столбцов матрицы являются также и базисными столбцами расширенной матрицы . По теореме о базисном миноре (1.6) последний столбец матрицы будет некоторой линейной комбинацией базисных столбцов основной матрицы. Тогда, в силу теоремы 1.5, последний столбец расширенной матрицы является линейной комбинацией и всех остальных столбцов матрицы . Поэтому существуют такие числа , что справедливы равенства (3.1.9). Но эти равенства означаю, что числа представляют собой решение системы уравнений (3.1.1), т.е. эта система является совместной. Теорема доказана.
Теорема Кронекера – Капелли устанавливает необходимое и достаточное условие совместности линейной системы уравнений, но не дает способа нахождения его решения.
