§8. Круговая диаграмма полных сопротивлений

Оказывается, что всё многообразие режимов, возникающих в нагруженной ЛП без потерь, можно отобразить на круговой диаграмме полных сопротивлений (диаграмме Смита).

Для некоторой нагруженной ЛП без потерь можно записать выражение для комплексной амплитуды колебания в произвольной точке с координатой ℓ:

Ú(ℓ)= Ú_пад(ℓ) + Ú_отр(ℓ) = Ú_{0 пад}e^iγℓ + ГÚ_{0 пад}e^{- iγℓ} (1.75)

Отношение комплексных амплитуд отражённой и падающей волн в произвольном сечении ЛП называют текущим коэффициентом отражения Г_ℓ ,

Г_ℓ = Гe^{- i2βℓl}

Текущий коэффициент отражения позволяет выразить напряжение и ток в ЛП таким образом:

Ú(ℓ) = Ú_пад (1 + Г_ℓ); ĺ(ℓ) = - ( Ú_пад/ Z_в)(1 - Г_ℓ) ,

откуда следует формула, связывающая Г_ℓ с нормированным входным сопротивлением ЛП, имеющей длину ℓ:

Z^н_вх = (1 + Г_ℓ) / (1 - Г_ℓ) = - Ú(ℓ) / Z_вĺ(ℓ) (1.76)

Соотношения (1.76) можно представить векторной диаграммой. Для этого комплексное число Г_ℓ геометрически отображается вектором длиной |Г|, который с ростом ℓ вращается по часовой стрелке (фазовый угол Г_ℓ должен уменьшаться). Числитель (1.76) пропорционален текущей амплитуде напряжения, а знаменатель – текущей амплитуде тока. Поэтому для построения векторной диаграммы напряжения и тока в ЛП нужно, отложив на плоскости горизонтальный вектор единичной длины (он соответствует амплитуде падающей волны), геометрически сложить его с двумя вращающимися векторами Г_ℓ и -Г_ℓ .

Последовательность векторных диаграмм, соответствующих различным длинам ℓ, представлена на рис.1.10а. Пусть при ℓ = 0 фаза коэффициента отражения от нагрузки такова, что векторная диаграмма имеет вид, изображённый на рис.1.10а Здесь фаза напряжения на нагрузке опережает фазу тока в ней , что свидетельствует об индуктивном характере нагрузки. Перемещаясь вдоль ЛП по направлению к генератору , будем вращать вектор Г_ℓ по часовой стрелке на угол 2βℓ. При этом неизбежно возникает случай горизонтального расположения вектора Г_ℓ (рис.1.10б). В этой точке ЛП напряжения падающей и отражённой волн сложатся синфазно, а токи этих волн противофазны. Следовательно, в такой точке возникают пучность напряжения и узел тока; входное сопротивление отрезка линии такой длины чисто вещественно, а нормированное входное Z^н_вх численно равно КСВН (по (1.76)).

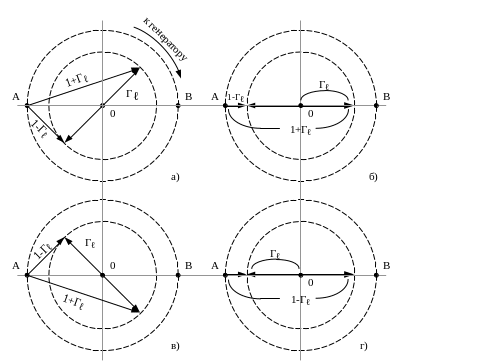
Рис 1.10

С дальнейшим увеличением ℓ изменяется порядок следования векторов напряжения и тока, так что входное сопротивление приобретает емкостной характер (рис.1.10.в). Продолжая вращение вектора Г_ℓ , приходим к противофазному сложению напряжений и синфазному сложению токов (рис.1.10г), то есть к точке с узлом напряжения и пучностью тока. Нормированное входное сопротивление в этом случае вещественно и равно отношению 1/ КСВН . Периодичность функции Г_ℓ приводит к тому, что полный оборот на векторной диаграмме будет совершён при перемещении вдоль ЛП на расстояние , равное половине длины волны, распространяющейся в ЛП.

Обозначим на диаграмме характерные точки. Точка О называется точкой согласования, поскольку ей соответствует нулевой коэффициент отражения. В точке А имеем Г = - 1, U = 0, I = 1 – Г = 2, и следовательно, входное сопротивление линии оказывается равным нулю. Поэтому точку А называют точкой короткого замыкания. Подобное рассуждение приводит к выводу, что точку В следует назвать точкой холостого хода (U = 2, I = 0 ). Диаметр АВ есть геометрическое место точек, соответствующих таким режимам работы ЛП, когда напряжения и ток синфазны. Поэтому этот отрезок называют линией активных входных сопротивлений (реактивные составляющие отсутствуют).

Окружность единичного радиуса с центром в точке О есть геометрическое место точек чисто реактивных входных сопротивлений, так как для каждой точки этой окружности сдвиг фазы между напряжением и током составляет 90° в соответствии с теорией об угле при вершине вписанного треугольника, опирающегося на диаметр.

Наконец, любую окружность с центром в точке О и произвольным радиусом, меньшим единицы, называют окружностью постоянного КСВН. Такая окружность соответствует постоянному модулю коэффициента отражения, остающемуся неизменным при изменении длины ЛП.

С помощью формулы (1.76) свяжем текущий коэффициент отражения непосредственно с нормированным входным сопротивлением отрезка ЛП заданной длины, нагруженного на известное комплексное сопротивление. В теории функций комплексного переменного формула вида (1.76) представляет дробно – линейное преобразование. В нашем случае осуществляется преобразование комплексной плоскости текущего коэффициента Г_l = ξ + iη в комплексную плоскость нормированных входных сопротивлений

Z^н_вх = R^н_вх +iX^н_вх .

Дробно – линейное преобразование обладает важным свойством: любая окружность в плоскости Г_ℓ переводится им тоже в некоторую окружность плоскости Z^н_вх (частный случай окружности – бесконечная прямая). Это преобразование обладает также свойством конформности – оно сохраняет неизменными значения углов между любыми пересекающимися линиями.

Координатная сетка в плоскости Z^н_вх состоит из двух ортогональных семейств прямых вида R^н_вх = const и X^н_вх = const. Можно утверждать, что на плоскости коэффициента Г_ℓ , то есть на векторной диаграмме, описанной выше, эта сетка примет вид двух семейств окружностей, ортогональных друг другу. Круговой диаграммой полных сопротивлений называется векторная диаграмма на плоскости комплексного коэффициента отражения, снабжённая координатной сеткой R^н_вх = const и X^н_вх = const.

Рассмотрим принцип построения этой сетки. Формулу (1.76) запишем

R^н_вх + iX^н_вх = ((1 + ξ) +iη)/ ((1 – ξ) – iη) = ((1 +ξ)+ iη)((1- ξ)+iη)/((1-ξ)² + η²) .

После разделения вещественной и мнимой частей получим равенства:

R^н_вх = ( 1 - ξ² - η²)/((1 – ξ)² + η²) ; (1.77)

X^н_вх = 2η / ((1 – ξ )² + η²) , (1.78)

которые являются уравнениями координатных линий Z^н_вх в плоскости Г_l .

Представим уравнение (1.77) в следующих модификациях:

R^н_вх(1 – ξ)² + R^н_вхη² +ξ² +η² - 1 = 0

ξ² + η² - 2R^н_вхξ/(1 + R^н_вх) = (1 – R^н_вх)/(1 + R^н_вх)

(ξ – R^н_вх/(1 + R^н_вх))² + η² = 1/ (1 + R^н_вх)² (1.79)

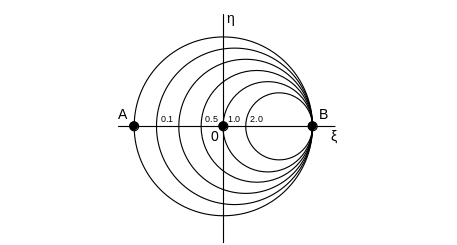
Рис 1.11.

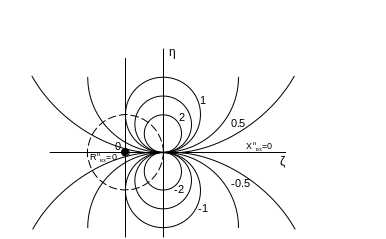
Рис 1.12.

Выведено уравнение семейства окружностей, представляющих собой геометрические места постоянных активных частей входного сопротивления отрезка ЛП. Центр любой окружности семейства находится в точке с координатами ξ = R^н_вх/(1 + R^н_вх), η = 0; при этом радиус окружности определяется величиной 1/ (1 + R^н_вх). На рис.1.11 показаны некоторые из таких окружностей, соответствующие положительным значениям R^н_вх . Отметим два обстоятельства:

1. Положительным значениям R^н_вх соответствуют окружности, целиком лежащие внутри круга с единичным радиусом. Иными словами, дробно – линейное преобразование (1.76) позволяет отобразить правую полуплоскость комплексной переменной Z^н_вх на внутреннюю область единичного круга, лежащего в плоскости переменной Г_ℓ. Остальная часть плоскости в данном случае игнорируется, так как она соответствует нагружению отрезка ЛП не на пассивный двухполюсник, а на источник колебаний (генератор).

2. Все окружности для разных R^н_вх касаются друг друга в точке холостого хода ( ξ = 1, η = 0). При R^н_вх>> 1 наблюдается резкое сжатие масштаба круговой диаграммы сопротивлений (КДС) вблизи точки холостого хода, что приводит к ограничению точности графических построений. Очевидно, что повышение точности может быть достигнуто за счёт увеличения масштаба части КДС, например, в области круга R^н_вх = 2.

Аналогичным образом уравнение (1.78) приводится к уравнениям окружностей:

(ξ – 1)² + (η – 1/X^н_вх)² = 1/(X^н_вх)². (1.80)

Окружности этого семейства имеют радиусы 1/(X^н_вх)²; центры их расположены в точках с координатами ξ = 1, η = 1/X^н_вх .

Соответствующие графики (рис.1.12) показывают, что окружности постоянных реактивных частей входного сопротивления располагаются по – разному в зависимости от знака X^н_вх : индуктивным величинам соответствует верхняя полуплоскость, емкостным – нижняя. Здесь же штриховой линией нанесена окружность единичного радиуса, ограничивающая интересующую нас область на плоскости.