§5.Типы волн в передающих линиях

Анализ общего случая распространения волн по ЛП показывает, что существует два класса волн:

1 – имеют только поперечные составляющие; не обладают дисперсией; не имеют критической частоты (конечной критической длины волны) и могут распространяться на любых частотах, включая постоянный ток. Такие волны называют поперечными электромагнитными, или волнами ТЕМ.

Для волн типа ТЕМ выражения для поперечных составляющих следуют из (2.28) – (2.33) при условии Е_z = 0 и Н_z = 0:

Е_х = - (iγ/ωεε₀)·Н_у; Е_у = (iγ/ωεε₀)·Н_х; (2.38) , (2.39)

Н_х = (iγ/ωμμ₀)·Е_у; Н_у = (iγ/ωμμ₀)·Е_х; (2.40) , (2.41)

2 – имеют помимо поперечных продольные составляющие поля; обладают дисперсией; характеризуются критической длиной волны λ_кр (частота f_кр), так что распространение возможно только на частотах, удовлетворяющих условию f > f_кр ( λ < λ_кр).

Волны с продольной составляющей H_z при Е_z = 0 называются поперечными электрическими волнами, а также волнами типа ТЕ (или типа Н ). Волны с продольной составляющей E_z при Н_z = 0 называются поперечными магнитными волнами, а также волнами типа ТМ (или типа Е).

Для волн типа ТЕ (Е_z = 0) имеем:

Е_х = (- iωμμ₀/(k² + γ²))·∂H_z/∂y; E_y = (iωμμ₀/(k² + γ²))·∂H_z/∂x; (2.42) , (2.43)

H_x = ( - γ/(k² + γ²))·∂H_Z/∂x; H_y = ( - γ/(k² + γ²))·∂H_Z/∂y; (2.44) , (2.45)

Для волн типа ТМ ( Н_z = 0) имеем:

Е_x = ( - γ/(k² + γ²))·∂Е_Z/∂x; Е_у = ( - γ/(k² + γ²))·∂Е_Z/∂у; (2.46) , (2.47)

H_x = (iωεε₀/(k² + γ²))·∂Е_Z/∂у; H_у = ( -iωεε₀/(k² + γ²))·∂Е_Z/∂x; (2.48) , (2.49)

§6.Волны в прямоугольном волноводе

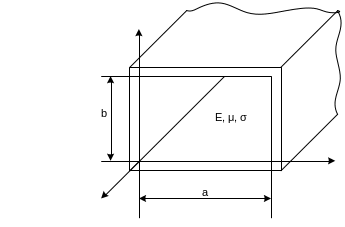
Рис 2.3.

Прямоугольный волновод наиболее часто применяется на практике из всей номенклатуры металлических волноводов и в общем виде соответствует геометрии, представленной на рис.2.3. Считаем, что волновод заполнен однородным изотропным диэлектриком без потерь (σ = 0). Потери в стенках тоже не будем учитывать, что приводит к условию бесконечной проводимости стенок (σ_ст = ∞), или их нулевого сопротивления. Указанные допущения оправданы для большинства практических случаев. Главное же состоит в том , что при условии σ = 0 и σ_ст = ∞ можно получить чёткое математическое описание электромагнитных волн, распространяющихся в волноводе, и на его основе – важные закономерности этих волн. Учёт же вносимых потерь энергии из- за конечных проводимостей σ и σ_ст легко осуществляется как отдельная операция, выполняемая на основе протабулированных значений погонных коэффициентов затухания (то есть величин α).

Общее решение волнового уравнения, выполненное в §2, даёт возможность определить все составляющие электрического и магнитного полей бегущей волны по формуле (2.17)

L = Dcos(ξx – φ)cos(ηy – ψ)exp(iωt – γz)

или

L = D((cos/sin(ξx))·(cos/sin(ηy))·exp(iωt – γz) (2.50)

Вспомним , что постоянная γ , определяющая в волноводе длину волны, фазовую скорость и затухание волны имеет вид (2.14):

γ² = - κ² + ξ² + η² .

Согласно общей теории по не имеющему внутренних проводников волноводу могут распространяться волны типов ТЕ и ТМ, волна же типа ТЕМ в таком волноводе существовать не может. Поэтому поле внутри волновода описывается десятью уравнениями вида (2.27) относительно составляющих Е_х, Е_у, Н_х, Н_у и Е_z или Н_z, каждое из которых содержит пять независимых констант (D, ξ, η, φ, ψ). Следовательно, задача заключается в определении 25 констант для волн типа ТЕ(Н) и 25 констант для волн типа ТМ (Е). Эти постоянные могут быть найдены при задании граничных условий, то есть значений векторов Е и Н на стенках волновода. При наложении условия σ_ст = ∞ тангенциальная (касательная) составляющая электрического поля на стенках должна быть равна нулю , то есть Е_t = 0.

Количество подлежащих определению постоянных может быть уменьшено, поскольку поперечные компоненты поля в соответствии с (2.34) – (2.37) однозначно связаны с продольными составляющими. Значит, для получения уравнений волн ТЕ и ТМ можно ограничиться нахождением всего десяти констант.

6.1Составляющие поля для волн типа ТМ. Эти составляющие определяются формулами (2.46) – (2.49), а которых выражения для продольной составляющей электрического поля Е_z должно соответствовать общему решению (2.50) скалярного волнового уравнения:

Е_z = D₁cos(ξx – φ)cos(ηy – ψ), ( 2.51)

Где D₁ – амплитудный множитель.

Подставив (2.51) в (2.46) – (2.49) и выполнив дифференцирование, получим:

E_x = D₁(ξγ/(κ² + γ²))·sin(ξx – φ)cos(ηy – ψ)·exp(iωt – γz); (2.52)

Е_y = D₁(ηγ/(κ² + γ²))·cos(ξx – φ)sin(ηy – ψ)·exp(iωt – γz); (2.53)

H_х =-iD₁(ωεε₀/(κ² + γ²))·cos(ξx – φ)sin(ηy – ψ)·exp(iωt – γz); (2.54)

Hy = iD₁(ωεε₀/(κ² + γ²))·sin(ξx – φ)cos(ηy – ψ)·exp(iωt – γz); (2.55)

Если обозначить D = D₁/(κ² + γ²) и опустить во всех выражениях множитель exp(iωt – γz), можно (2.52) – (2.55) переписать таким образом:

Е_х = Dγξsin(ξx – φ)cos(ηy – ψ); (2.56)

Е_y = Dγηcos(ξx – φ)sin(ηy – ψ); (2.57)

Е_z = D(κ² + γ²)cos(ξx – φ)cos(ηy – ψ); (2.58)

H_х =-iDωεε₀ηcos(ξx – φ)sin(ηy – ψ); (2.59)

H_х =iDωεε₀ξsin(ξx – φ)cos(ηy – ψ); (2.60)

H_z = 0.

В уравнения (2.56) – (2.60) входят пять независимых констант ξ, η, φ, ψ, D. Обращаясь к рис.2.3, запишем граничные условия для волновода в виде:

Е_х = 0 при у = 0 ; у = b ; Е_у = 0 при х = 0 ; х = a ;

Е_z = 0 при х = 0 ; у = 0 ; х = a ; у = b .

Если Е_х = 0 при любых значениях x, то cos(ηy – ψ) = 0. Полагая у = 0 , получаем cosψ = 0; ψ = π/2 + pπ, где p = 0, 1, 2, … В дальнейшем ограничимся решением ψ = π/2, так как при p > 0 происходит лишь одновременное изменение знака при всех составляющих поля (2.56) – (2.60). Полагая y = b с учётом ψ = π/2, получаем sinηb = 0; ηb = nπ, откуда η = nπ/b, n = 0, 1, 2, … Подобным образом находим постоянные ξ и φ: φ = π/2 и ξ = mπ/a, m = 0, 1, 2, …

Таким образом, определены четыре независимых постоянных, условие Е_z = 0 на стенках волновода не даёт новых решений.

Что касается постоянной D, то она может быть вычислена только при дополнительных условиях (например, при задании передаваемой по волноводу мощности). Однако как видно из уравнений (2.56) – (2.60), в определении структуры поля величина D роли не играет.

Постоянная распространения γ определится теперь так:

γ² = - k² + π²(m²/a² + n²/b²) ( 2.61)

Окончательно компоненты волн типа ТМ в прямоугольном волноводе могут быть представлены в таком виде:

Е_х = - Dγ(πm/a)cos(πmx/a)sin(πny/b); (2.62)

Е_х = - Dγ(πn/b)sin(πmx/a)cos(πny/b); (2.63)

Е_х =Dπ²(m²/a² + n²/b²)sin(πmx/a)sin(πny/b); (2.64)

H_х = iDωεε₀(πn/b)sin(πmx/a)cos(πny/b); (2.65)

H_y = - iDωεε₀(πm/a)cos(πmx/a)sin(πny/b); (2.66)

В каждом из этих уравнений подразумевается множитель exp(iωt – γz), определяющий распространение волны по направлению оси z и гармонический вид колебаний во времени.

Если положить γ = iβ и умножить все уравнения в правой части на i (что соответствует лишь сдвигу начала отсчёта координаты z на четверть длины волны в волноводе без изменений структуры поля), то амплитудные коэффициенты в (2.62) – (2.66) преобразуются в соответствующие величины: Dβ, Dβ, iD, - D, D. Множитель exp(iωt – γz) приобретает вид expi(ωt – βz), где

β = k² - π²(m²/a² + n²/b²). (2.67)

Решение показывает, что в общем случае в прямоугольном волноводе может распространяться бесконечное множество волн типа ТМ, отличающихся множителями m и n, Поэтому принято при обозначении волны в индексе указывать значения m и n, то есть ТМ_mn (Е_mn). Равенство m и n нулю неприемлемо, так как при этом все компоненты обращаются в ноль.Поэтому волны ТМ₀₀(Е₀₀), ТМ_0n(Е_0n) и ТМ_m0(Е_m0) в рассматриваемом волноводе не существуют. Простейшей волной ТМ – типа является волна ТМ₁₁(Е₁₁). Далее следуют волны Е₁₂, Е₂₁, Е₂₂ и т.д. до бесконечности.

Отрицательные значения m и n, допустимые с математической точки зрения, не дают новых решений, а лишь изменяют знак у всех составляющих, что может быть учтено при вычислении постоянной D.

6.2Составляющие поля для волн типа ТЕ. Пользуясь методикой, такой же, как в п.6.1, можем записать

Н_z = D₁cos(ξx – φ)cos(ηy – ψ) , (2.68)

не предполагая равенства соответствующих констант для волн типов ТМ и ТЕ. Подставляя (2.68) в (2.42) – (2.45), получаем

Е_х = iD₁η(ωμμ₀/(k² + γ²))cos(ξx – φ)sin(ηy – ψ); (2.69)

E_y = -iD₁ξ(ωμμ₀/(k² + γ²))sin(ξx – φ)cos(ηy – ψ); (2.70)

H_х = D₁ξ(γ/(k² + γ²))sin(ξx – φ)cos(ηy – ψ); (2.71)

H_х = D₁η(γ/(k² + γ²))cos(ξx – φ)sin(ηy – ψ); (2.72)

где для краткости опущен множитель exp(iωt – γz).

На основании граничных условий (см. п.6.1) получаем

φ = 0; ψ = 0; ξ = πm/a; η = πn/b,

где m и n могут быть любыми целыми чилами и равными нулю.

Отметим, что поперечные константы η и ξ совпадают с таковыми для волн типа ТМ. Поэтому совпадают и выражения для постоянной γ и фазовой постоянной β. Используя найденные постоянные и обозначая D = D₁μμ₀/(k² + γ²) запишем окончательно:

Е_х = Dω(πn/b)·cos(πmx/a)·sin(πny/b) ; (2.73)

Е_y = -Dω(πm/a)·sin(πmx/a)·cos(πny/b) ; (2.74)

H_х = -iD(γ/μμ₀)(πm/a)·sin(πmx/a)·cos(πny/b); (2.75)

H_х = -iD(γ/μμ₀)(πn/b)·cos(πmx/a)·sin(πny/b); (2.76)

H_z = -iD(π²/μμ₀)(m²/a² + n²/b²)·cos(πmx/a)·cos(πny/b); (2.77)

При пренебрежении потерями в волноводе γ = iβ, и коэффициенты амплитуды –iDγ преобразуются в Dβ.

Очевидно существование бесконечного количества волн типа ТЕ(Н), они обозначаются ТЕ_mn(Н_mn). Волна типа Н₀₀ невозможна, однако волны Н_m0 и Н_0n существуют и являются более простыми по структуре.

Особо важную роль в технике СВЧ играет волна Н₁₀ , для которой m = 1 и n = 0, так что компоненты поля имеют вид :

Е_у = -D(ωπ/a)·sin(πx/a); Е_х = Е_z = 0; Н_y = 0;

Н_х = D(βπ/μμ₀a)·sin(πx/a); Н_z = - iD(π²/μμ₀a²)·cos(πx/a).

Таким образом, по однородному прямоугольному волноводу в принципе могут распространяться магнитные волны Н₁₀, Н₀₁, Н₂₀, Н₀₂, …, Н₁₁, Н₁₂, Н₂₂ и т.д. до бесконечности.

6.3 Структуры полей в прямоугольном волноводе.

- Для волн типа ТМ Н_z = 0, поэтому магнитные силовые линии есть плоские кривые, лежащие в поперечном сечении волновода, в то время как электрические силовые линии имеют все три составляющие и являются пространственными кривыми.

Для волны Е₁₁ m = 1 и n = 1, тогда

Н_х ~ sin(πx/a)·cos(πy/b); H_y ~ cos(πx/a)·sin( πy/b).

Очевидно, что Н_х = 0 при у = b/2 и любом х, а Н_у = 0 при х = а/2 и любом у. Следовательно, силовые магнитные линии всюду нормальны к оси АА и к оси ВВ. Во всех прочих точках сечения присутствуют обе составляющие магнитного поля, изменяющиеся по кривым, показанным на рис.2.4. В результате магнитные линии приобретают форму искажённых эллипсов, стремящихся вблизи стенок к прямоугольнику.

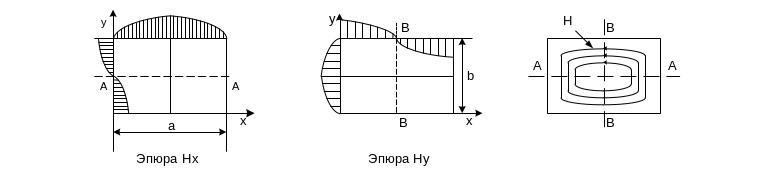
Рис 2.4.

В продольном сечении волновода по оси z напряжённость магнитного поля при t = const изменяется по синусоидальному закону в соответствии с множителем expi(ωt – βz). Расстояние между максимумами Н равно λ_в/2.

Для определения формы электрических силовых линий волны Е₁₁ находим:

Е_х ~ cos(πx/a)·sin(πy/b); E_y ~ sin(πx/a)·cos(πy/b); E_z ~ isin(πx/a)·cos(πy/b).

Эпюры распределения электрического поля в поперечном и продольном сечениях показаны на рис.2.5. Наличие множителя i в формуле для Е_z говорит о сдвиге максимума Е_z по оси z относительно максимума Е_х и Е_у на π/2, то есть на четверть длины волны в волноводе, так как множитель i может быть представлен как exp(iπ/2). Следовательно, при составляющей Е_z имеется множитель expi(ωt – βz^'), где z^' = z – λ_в/4.

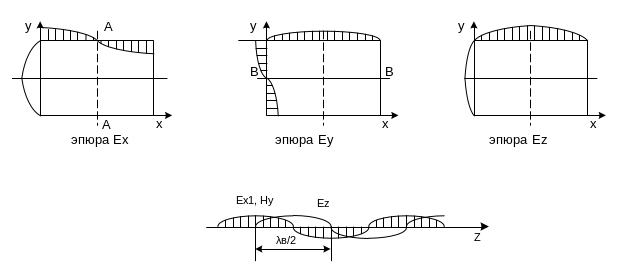
Рис 2.5.

По виду эпюр на рис.2.5 можно заключить, что электрические силовые линии в сечениях АА и ВВ целиком лежат в плоскостях, проходящих через эти оси и параллельных оси z. Продольная составляющая Е_z, равная нулю на поверхности волновода, увеличивается по мере удаления от стенки. В результате этого силовые линии выходят из плоскости XY. Соответствующее изображение электрических силовых линий в поперечном и продольном сечениях показано на рис.2.6.

Рис 2.6.

Для учёта магнитных составляющих надо принять во внимание синфаз ность всех поперечных составляющих и сдвиг на π/2 (из-за множителя i ) для продольной составляющей Е_z. Максимумы поперечного магнитного поля совпадают с максимумами поперечного электрического поля, что соответствует режиму бегущей волны в волноводе, энергия которой перемещается в направлении оси волновода.

Картины электромагнитных полей для бегущих волн типа Е_mn, когда значения m и n больше единицы, получаются мультиплицированием картины поля волны Е₁₁ (рис.2.6). Так для волны Е₂₁ будем иметь две ячейки типа рис.2.6 по оси x (на стороне a волновода), для волны Е₂₂ - четыре ячейки типа рис.2.6, расположенные в виде матрицы 2х2 по сторонам a и b волновода соответственно, для волны Е₄₃ – двенадцать ячеек, расположенных в виде матрицы 4х3 по сторонам a и b , и т.д. Следовательно, числа m и n показывают количество пространственных полупериодов (вариаций) поля по соответствующим осям координат или число простейших ячеек поля вдоль соответствующей стороны прямоугольного волновода.

- Для волн типа ТЕ Е_z = 0 и электрическое поле всегда лежит в плоскости, нормальной к оси волновода, а магнитные силовые линии всегда являются пространственными кривыми.

Вначале рассмотрим простейшую волну Н₁₀, для которой

E_y ~ sin(πx/a); H_x ~ sin(πx/a); H_z ~icos(πx/a); E_x = E_{z = 0;} H_y = 0.

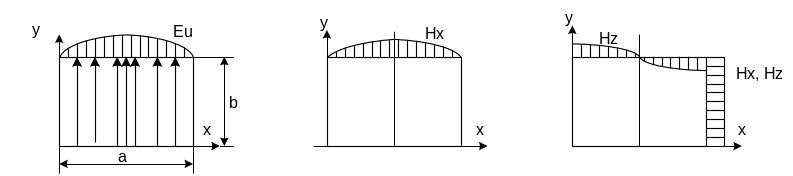
Рис 2.7. Рис 2.8.

На рис.2.7 построена эпюра электрического поля в поперечном сечении. Вариации поля вдоль стороны b отсутствуют, а вдоль стороны a оно изменяется по синусоидальному закону. На этом же рисунке показана структура поля Е. Структура магнитного поля волны Н₁₀ выясняется из эпюр, приведённых на рис.2.8. Магнитные линии имеют форму, похожую на эллипсы, и располагаются целиком в плоскости ХZ, как показано на рис.2.9. Максимум продольной составляющей Н_z смещён вдоль оси z относительно поперечной составляющей Н_х на λ_в/4. Совмещённая картина электрического и магнитного полей бегущей волны Н₁₀ приведена на рис.2.10. Здесь, как и в случае Е – волн, максимумы поперечных составляющих полей обязательно совпадают. Волны типов Н₂₀, Н₃₀ и т. д. имеют соответственно две три и болоее вариаций поля по стороне a. Волна типа Н₀₁ отличается от волны Н₁₀ лишь положением плоскости поляризации (на 90°).

Рис 2.9. Рис 2.10

Магнитные волны Н_mn с индексами m>0 и n>0 имеют более сложную структуру поля. На рис.2.11 показана структура волны Н₁₁ в поперечном сечении волновода. Структуры волн более высокого порядка можно построить, учитывая, что числа m и n здесь тоже указывают на количество вариаций поля по соответствующей оси. Поэтому для описания волны типа Н в прямоугольном волноводе необходимо знать только две простейшие ячейки: первая соответствует волне Н₁₀, вторая – волне Н₁₁.

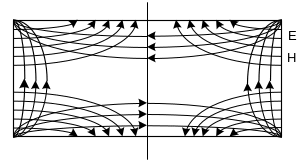
Рис 2.11.

Отметим, что для волн Н₁₀, Н₁₁, Н₂₁ т т.д. в волноводе можно найти плоскости, во всех точках нормальные к линиям Е и касательные к линиям Н. Следовательно, поле данной волны не будет возмущено, если в волноводе расположить тонкие идеально проводящие поверхности, совпадающие с этими плоскостями. В результате волновод с волной Н₁₀может быть разделён на сколь угодно большое число волноводов с неизменным размером a и уменьшенным размером b. В случае волны Н₁₁ волновод разделяется на треугольные ячейки, по которым независимо распространяются электромагнитные волны. При удалении любой из ячеек возникает волновод с формой сечения, значительно отличающейся от прямоугольной, но с такой же критической длиной волны. Сказанное иллюстрируется рис.2.12.

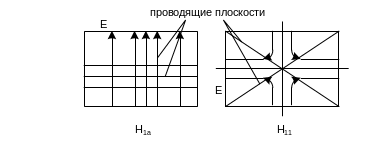
Рис 2.12.

В некоторых случаях введение дополнительных проводящих плоскостей позволяет исключить распространение нежелательного типа волны.

6.4.Токи в стенках прямоугольного волновода.

Из общих электротехнических принципов следует, что по внутренним поверхностям стенок должны протекать высокочастотные токи, структура которых непосредственно связана со структурой поля в волноводе.

На рис.2.13 изображены стенка волновода и отрезок магнитной линии, касательной (тангенциальной) к этой стенке.

Рис 2.13.

Рассмотрим прямоугольный замкнутый контур длиной dℓ, охватывающий магнитный вектор Н_t у стенки и Н´_t внутри стенки. По закону полного тока, обходя штриховой контур, получаем ток проводимости, нормальный к поверхности контура:

dl = |Н_t - Н´_t|dℓ

Направление тока определяется правилом буравчика. Далее запишем

J = dl/dℓ = |Н_t - Н´_t| , (2.78)

где J – плотность поверхностного тока в стенке волновода, А/м.

Распространяя контур на рис.2.13 достаточно далеко внутрь металла, где Н´_t→0, то есть охватывая весь поверхностный ток, имеем

J = |Н_t| (2.79)

В соответствии с правилом буравчика заключаем, что продольный ток J_z обусловлен поперечными составляющими магнитного поля Н_х и Н_у , а токи поперечные J_х и J_у определяются составляющей Н_z.

Глубина проникновения поля в металл δ определяется по уравнению поверхностного эффекта

Δ = (2 /ωμ_стμ₀σ_ст)^0.5 (2.80)

Где σ_ст и μ_ст – активная проводимость материала стенки и его относительная магнитная проницаемость. Когда стенки выполнены из материалов с большой σ_ст (Cu, Ag), толщина δ очень мала и обычно составляет единицы и доли мкм на частотах (10⁹ – 10¹⁰)Гц.

Рассмотрим токи в стенках прямоугольного волновода. У волны типа ТМ(Е) из-за отсутствия продольной составляющей Н_z поперечные токи в стенках волновода отсутствуют:

J_х = J_у = 0.

Для продольных токов в широкой стенке J(a) и узкой стенке J(b) получаем:

J_z(a) = Н_х при у = 0, у = b; (2.81)

J_z(b) = H_y при х = 0, х = a. (2.82)

Используя уравнения для волн типа Е_mn, имеем:

J_z(a) ~sin(πmx/a); J_z(b) ~ sin(πn/b).

Нетрудно видеть, что токи имеют максимумы в середине каждой стороны волновода (х = a/2 и у = b/2) и равны нулю на рёбрах для волны Е₁₁. Вдоль оси z изменение токов происходит по гармоническому закону в соответствии с множителем exp(-iβz), где β = 2π/λ_в.

Отметим, что в стенках волновода могут быть прорезаны узкие щели, параллельные оси z. Распространение волны Е₁₁ (и других волн типа Е) при этом принципаиально не нарушается. Всякая же поперечная щель должна сильно возмутить поле в волноводе, поскольку она нарушает линии тока в стенках.

Построение линий тока при волнах Е₁₂, Е₂₂ и т.д. проводится аналогично по известным структурам магнитного поля.

Обратимся к токам магнитных волн Н. У таких волн имеются все три составляющие магнитного поля, поэтому должны быть в общем случае как продольные, так и поперечные токи. Продольные токи могут быть определены из соотношений (2.81) и (2.82). Плотность поперечных токов зависит от составляющей Н_z :

J_х(a) = Н_z при у = 0 и при у = b; (2.83)

J_у(b) = Н_z при х = 0 и при х = a. (2.84)

Более подробно рассмотрим простейшую волну Н₁₀. Согласно уравнениям для компонент этой волны с учётом направления по правилу буравчика имеем:

J_z(a) = ±D(βπ/μμ₀a)·sin(πx/a); J_z(b) = 0 ; (2.85) , (2.86)

J_x(a) = ±D(π²/μμ₀a²)·cos(πx/a); J_y(b) = iD(π²/μμ₀a²); (2.87) , (2.88).

Рис 2.14.

Эпюры распределения токов по (2.85) – (2.88) плказаны на рис2.14. В узкой стенке волновода продольные токи отсутствуют. Поперечный ток в узкой стенке в фиксированном сечении вариаций не имеет. Следовательно, любая продольная щель в узкой стенке должна сильно возмущать поле волны Н₁₀. Напротив, узкая поперечная щель в боковой стенке b не должна влиять на структуру и распространение волны.

Обратим внимание на то , что поперечный ток J_х(a) в середине широкой стенки при х = a/2 равен нулю. Следовательно, продольная щель , прорезанная точно в середине широкой стенки, не должна влиять на распространение волны Н₁₀. Такие щели используются в волноводной технике для зондовых измерений стоячих волн.

Построение эпюр и картин паспределения токов для волн Н₀₁, Н₂₀, Н₁₁ и т.д. не представляет труда по рассмотренным ранее структурам полей в волноводе.

6.5.Критическая длина волны и диспесия волн в прямоугольном волноводе.

Условием распространения волн Е и Н типов является неравенство λ < λ_кр, где λ_кр – измеренная в свободном пространстве длина волны, при которой прекращается распространение волны конкретного типа по волноводу. Согласно общему положению (2.14)

β² = k² - (ξ² + η²) (2.89)

В критическом режиме β = 0, и величина k, определяемая изь(2.23), при λ = λ_кр равна

k= (2π/λ_кр)·(εμ)^0.5 ;

принимая ε = μ = 1 (вакуумное наполнение) и полагая в (2.89) β = 0, получаем

λ_кр = 2π/(ξ² + η²)^0.5 (2.90)

Поперечные постоянные ξ и η совпадают для электрических и магнитных полей, поэтому выражение для критической длины волны является общим для волн Е и Н. Подставляя в (2.90) выражения для ξ и η, получаем важное уравнение:

λ_кр = 2 / ((m²/a²) + (n²/b²))^0.5 (2.91)

Уравнение (2.91) показывает, что λ_кр одно и то же для волн Е и Н при одинаковых значениях m и n. Такое событие называется вырождением. Следовательно, волны в прямоугольном волноводе обычно имеют двухкратное вырождение (исключение – волны Н_m0 и H_0n поскольку не существует волн Е_m0 и Е_0n).

Примеры: для волны Н₁₀ (m = 1; n = 0) λ_кр= 2a;

для волны Н₀₁ (m = 0; n = 1) λ_кр= 2b;

для волн Н₁₁ и Е₁₁ λ_кр = 2ab/(a² + b²) и т. д.

Волну, для которой λ_кр имеет наибольшее значение, называют низшей (основной) волной конкретного волновода. В прямоугольном волноводе λ_кр тем больше, чем меньше числа m и n. Пэтому низшей (основной) волной здесь является волна Н₁₀ (при a > b). Зная значение величины λ_кр, нетрудно найти длину волны λ_в и фазовую скорость V_ф.

Если при заданных размерах a и b необходимо использовать волновод на по возможности самых низких чатотах или, наоборот, необходимо получить наименьшие размеры сечения волновода для передачи энергии в заданной полосе частот, целесообразно использовать тип волны с наиболее возможной λ_кр. Очень важен выбор типа волны с точки зрения управления сигналом (воздействия на сигнал) при его прохождении по волноводному тракту: изменения амплитуды, преобразования по частоте, детектирования, изменения направления передачи и др., так как разработка устройств, воздействующих на сигнал в волноводе, базируется на одном определённом типе волны. Выбор для всех устройств волноводного тракта основного (низшего) типа колебаний (Н₁₀ для прямоугольного волновода) унифицирует устройства и с точки зрения рабочего диапазона частот.