
- •Математичні моделі в сапр: методичні вказівки до лабораторних робіт
- •Передмова до методичних вказівок
- •1.Лабораторна робота EvalExpr на тему "Знаходження похибок обчислень"
- •Теоретичні питання.
- •Приклад виконання роботи EvalExpr
- •Варіанти індивідуальних завдань до роботи EvalExpr
- •2.Лабораторна робота DetKram на тему “Розв’язання слр за формулами Крамера”
- •Теоретичні питання
- •Приклад виконання роботи DetKram
- •Варіанти індивідуальних завдань до роботи DetKram
- •Допоміжні матеріали до роботи DetKram Інструкція користувачу до додатку InteractiveDet
- •Приклад змісту вхідного файла Det.Inp:
- •Вихідні файли програми.
- •Натискання клавіші “Введення з файлу”.
- •Натискання клавіші “Зменшити у рядку”.
- •Натискання клавіші “Зменшити у стовпці”.
- •Натискання клавіші “Зменшити розміри”.
- •Завершення роботи додатку.
- •3.Лабораторна робота InvMatr на тему “Розв’язання слр за методом оберненої матриці”
- •Теоретичні питання
- •Приклад виконання роботи InvMatr
- •Варіанти індивідуальних завдань до роботи InvMatr
- •Допоміжні матеріали до роботи InvMatr Програма AdjMatr
- •Інструкція користувачу до додатку InteractiveAdjMatr
- •4.Лабораторна робота Gauss на тему „Наближене розв`язання слр методами виключення невідомих”
- •Теоретичні питання
- •Приклад виконання роботи Gauss
- •2В. Обчислення компонент вектора нев’язки.
- •3A. Знаходження наближеної оберненої матриці за методом Гауса.
- •3B. Знаходження компонент наближеного розв’язку .
- •3C. Знаходження компонент вектору нев’язки
- •5. Знаходження міри обумовленості головної матриці системи.
- •Варіанти індивідуальних завдань до роботи Gauss
- •Додаткові матеріали до роботи Gauss Програма NormVect знаходження різних норм вектора
- •Програма NormMatr знаходження різних норм матриці
- •Процедура g3v33l4
- •Модуль GaussRow
- •Iнструкцiя користувачу до програми InteractiveGauss
- •5.Лабораторна робота LinSysIt на тему “Ітераційні методи розв’язання слр”
- •Теоретичні питання
- •Приклад виконання роботи LinSysIt
- •Варіанти індивідуальних завдань до роботи LinSysIt
- •Допоміжні матеріали до роботи LinSysIt Програма NormForm
- •Програма SysIter
- •Програма Zeidel
- •6.Лабораторна робота TransEq на тему "Розв'язання трансцендентних рівнянь з одним невідомим"
- •Теоретичні питання
- •Приклад виконання роботи TransEq
- •Розрахункова таблиця знаходження кореня
- •Розрахункова таблиця знаходження кореня
- •Розрахункова таблиця знаходження кореня
- •Уточнення відокремленого кореня за методом простих ітерацій.
- •Розрахункова таблиця знаходження кореня рівняння за методом простих ітерацій
- •Розрахункова таблиця знаходження кореня рівняння за методом простих ітерацій
- •Варіанти індивідуальних завдань до роботи TransEq
- •Додаткові матеріали до роботи TransEq Інструкція користувачу для роботи з додатком TranscEq
- •Робота з додатком TranscEq
- •7.Лабораторна робота NonLinSys на тему „Розв’язання систем нелінійних рівнянь”
- •Теоретичні питання
- •Приклад виконання роботи NonLinSys
- •Розрахункова таблиця знаходження роз'вязку
- •Варіанти індивідуальних завдань до роботи NonLinSys
- •Допоміжні матеріали до роботи NonLinSys Інструкція користувачу для роботи з програмою Newton2
- •Текст програми Newton2
- •Текст модуля Funct
- •Текст модуля NewtonS
- •8.Лабораторна робота SelfEq на тему ”Знаходження характеристичного рівняння”
- •Теоретичні питання
- •Приклад виконання роботи SelfEq
- •Варіанти індивідуальних завдань до роботи SelfEq
- •9.Лабораторна робота SelfVect на тему “Знаходження власних векторів”
- •Теоретичні питання.
- •Приклад виконання роботи SelfVect
- •Варіанти індивідуальних завдань до роботи SelfVect
- •Література
4.Лабораторна робота Gauss на тему „Наближене розв`язання слр методами виключення невідомих”
Завдання: Розв'язати наближено СЛР за методом Гауса. Знайти відповідний наближений розв'язок. Знайти міри обумовленості СЛР для трьох векторних норм (норми максимуму, квадратичної та інтегральної норми).
Хід виконання. Дня заданої СЛР:
Записати її у матричному виді. Знайти головну та розширену матриці СЛР.
Розв'язати наближено СЛР за допомогою метода Гауса. Нехай
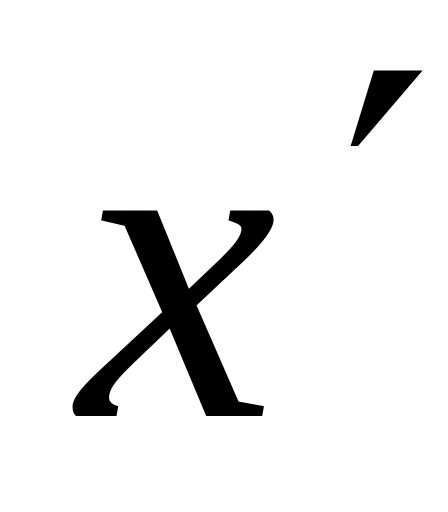 -
відповідний
наближений розв'язок і
-
відповідний
наближений розв'язок і
 - відповідний
вектор нев'язки.
- відповідний
вектор нев'язки.Знайти за методом Гауса наближену обернену матрицю
 і розв'язок СЛР.
Нехай
і розв'язок СЛР.
Нехай
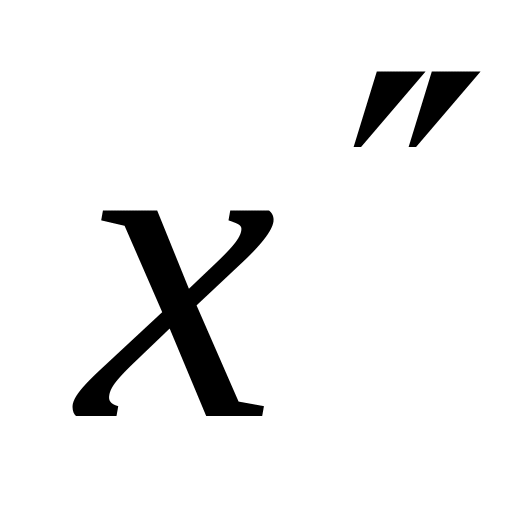 —
відповідний наближений розв'язок і
—
відповідний наближений розв'язок і
 відповідний вектор нев'язки.
відповідний вектор нев'язки.
Порівняти знайдені наближені розв'язки за допомогою відповідних векторів нев'язок
Знайти міри обумовленості
 головної матриці
системи
для різних векторних норм (норми
максимуму, квадратичної та інтегральної
норм).
головної матриці
системи
для різних векторних норм (норми
максимуму, квадратичної та інтегральної
норм).Знайти розв'язок СЛР за допомогою стандартної або за допомогою власної програми. Порівняти цей розв'язок з попередніми розв'язками.
Оформити звіт та захистити лабораторну роботу.
Теоретичні питання
Метод Гауса розв’язання СЛР. Головний та ведучий елементи у методах Гауса.
Нев'язка наближеного розв'язку та її використання.
Знаходження оберненої матриці за методом Гауса або Жордана-Гауса.
Знаходження рангу матриці за методом Гауса.
Норма вектора, та її властивості. Приклади векторних норм (норма максимуму, квадратичної та інтегральної норми).
Норма матриці та її властивості. Підлегла норма матриці. Приклади підлеглих норм матриць (для норми максимуму, квадратичної та інтегральної норм).
Погана обумовленість квадратних матриць і СЛР.
Приклад виконання роботи Gauss
Лабораторна робота Gauss на тему „Наближене розв`язання СЛР методами виключення невідомих”
Варіант 33. Виконав студент групи БІТ1-05, Усіков Микита Юрійович. Дата виконання: 15.10.2006.
Завдання. Розв’язати систему лінійних рівнянь
![]() (1.4.9)
(1.4.9)
за методом Гауса. Знайти наближену обернену матрицю до головної матриці системи за методом Гауса і за допомогою цієї матриці знайти відповідний наближений розв'язок. Порівняти одержані наближені розв’язки за допомогою відповідних векторів нев'язок та знайти міри обумовленості системи для трьох векторних норм (норми максимуму, квадратичної та інтегральної норми).
Виконання роботи.
1. Знаходження розширеної матриці системи. Додаючи до головної матриці системи (1.4.9)
 (1.4.10)
(1.4.10)
вектор-стовпець з правих частин, одержуємо розширену матрицю системи (1.4.9):
 (1.4.11)
(1.4.11)
2.
Знаходження наближеного розв'язку
![]() системи за методом Гауса.
Скористуємось програмою InteractiveGauss
(див.
далі відповідну інструкцію користувача),
у якій реалізовано
алгоритм Гауса з обранням головного
елементу серед елементів поточного
стовпця під головною діагоналлю.
При цьому виберемо
системи за методом Гауса.
Скористуємось програмою InteractiveGauss
(див.
далі відповідну інструкцію користувача),
у якій реалізовано
алгоритм Гауса з обранням головного
елементу серед елементів поточного
стовпця під головною діагоналлю.
При цьому виберемо
![]() (число знаків після коми, які потрібно
залишити при заокругленні). Відповідний
вхідний файл Gauss.inp
буде мати вигляд:
(число знаків після коми, які потрібно
залишити при заокругленні). Відповідний
вхідний файл Gauss.inp
буде мати вигляд:
------------------ початок ------------------

------------------- кінець ----------
2а. Прямій хід. Початкова матриця (1.4.11).
Цикл 1. Крок 1:
Пошук головного елемента у стовпці 1.
(Це![]() ).
).
Цикл 1. Крок 2: Переставлення 4 і 1 рядків.
 .
.
Цикл 1. Крок 3:
Ділення рядка 1 на число
![]() .
.
 .
.
Цикл 1. Крок 4:
Створення
нулів у стовпці 1 під
![]() :
:
 .
.
Цикл 2.Крок 1:
Пошук головного елемента у стовпці 2
(під
![]() включно). Це
включно). Це
![]()
Цикл 2. Крок 2: Переставлення рядків 2 і 2. Поточна матриця не змінюється.
Цикл 2. Крок 3: Ділення рядка 2 на число
 .
.
Цикл 2. Крок 4:
Створення нулів у стовпці 2 під
![]()
 .
.
Цикл 3. Крок 1:
Пошук головного елемента у стовпці 3
(під
![]() включно). Це
включно). Це
![]() .
.
Цикл 3. Крок 2: Переставлення рядків 3 і 4.
 .
.
Цикл 3. Крок 3:
Ділення рядка 3 на число
![]() .
.

Цикл 3.Крок 4:
Створення нулів у стовпці 3 під
![]()
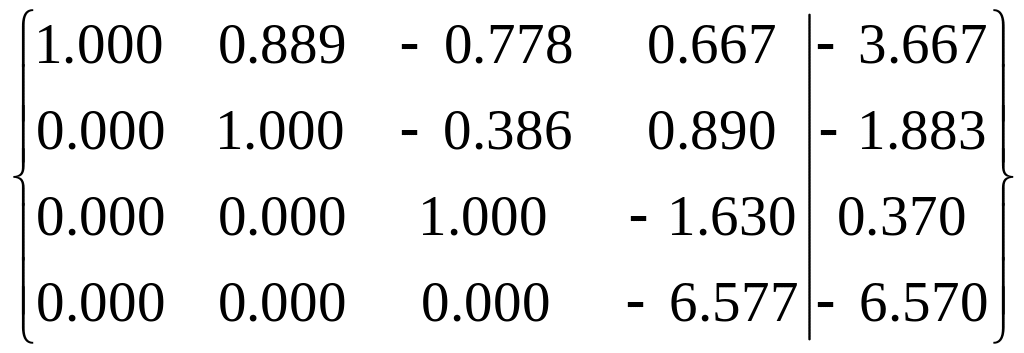
Цикл 4. Крок 1:
Пошук головного елемента у стовпці 4
(під
![]() включно). Це
включно). Це
![]()
Цикл 4. Крок 2: Переставляння рядків 4 і 4. Поточна матриця не змінюється.
Цикл 4. Крок 3:
Ділення рядка 4 на число
![]()

Головна матриця системи зведена до верхньої трикутної матриці. Прямий хід завершено.
2б. Обернений
хід.
Крок 1:
Створення нулів у стовпці 4 над![]()
 .
.
Крок 2:
Створення нулів у стовпці 3 над
![]()
 .
.
Крок 3:
Створення нулів у стовпці 2 над
![]()
 .
.
Отже, головна матриця системи зведена до одиничної матриці. Обернений хід закінчено.
При цьому, останній
стовпець останьої матриці містить
вектор наближеного розв’язку
![]() за методом Гауса. Тому
за методом Гауса. Тому
![]()
