Приклад виконання роботи TransEq

Лабораторна робота TransEq на тему "Розв'язання трансцендентних рівнянь з одним невідомим".

Варіант З1. Виконав студент групи БІТІ-04, Павлік Олексій Васильович. Дата виконання: 05.11.2003.

Завдання. По-перше, відокремити корінь рівняння , який має найменшу абсолютну величину серед всіх коренів цього рівняння, і знайти цей корінь з точністю за допомогою методів дихотомії, хорд і дотичних.

По-друге, відокремити корінь рівняння , який має найменшу абсолютну величину серед всіх коренів цього рівняння, представити рівняння в околі відокремленого кореня у вигляді і знайти цей корінь наближено з точністю за допомогою метода простих ітерацій із зупинками обчислень за числом ітерацій та за величиною поточного кроку.

Виконання роботи.

1. Відокремлення коренів рівняння . Легко перевірити, що не є коренем рівняння 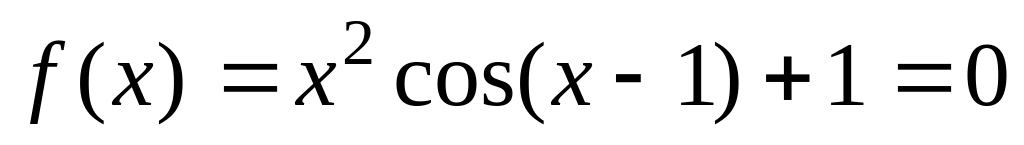. Тому можна поділити обидві частини цього рівняння на і отримати еквівалентне рівняння . Легко накреслити спільний малюнок графіків функцій і (креслення відповідного малюнку з графіками залишаємо студентові). З цього малюнку бачимо, що існує нескінченна кількість точок перетину цих графіків. Проекції на вісь цих точок дає корені рівняння . З того ж малюнку бачимо, що найменший за абсолютною величиною корінь належить інтервалу і він єдиний на цьому інтервалі.

Дійсно, легко перевірити, що , . Скористаємось додатком TranscEq, виконання якого показує, що на інтервалі функція змінює знак. У той же час бачимо, що функції і власного знаку не змінюють.

Проведемо аналітичну перевірку відокремлення кореня (на малюнку – найбільш близького до початку координат). Для цього підрахуємо значення функції у точках і :

,

.

Значення функції на кінцях інтервалу мають різні знаки. Тому на інтервалі є єдиний корінь рівняння .

2. Уточнення відокремленого кореня на інтервалі за методом дихотомії. Зведемо підрахунки у таблицю.

Таблиця 1.

Розрахункова таблиця знаходження кореня

рівняння за методом дихотомії.

1	2	3	4	5	6	7	8
0	-1.3	-0.126	-1.2	0.154	-1.25	0.085	0.1
1	-1.3	-0.126	-1.25	0.085	-1.275	-0.0525	0.05
2	-1.275	-0.0525	-1.25	0.085	-1.2625	-0.0167	0.025
3	-1.2625	-0.0167	-1.25	0.085	-1.25625	0.00098	0.0125
4	-1.2625	-0.0167	-1.25625	0.00098	-1.25938	-0.00782	0.00625
5	-1.25938	-0.00782	-1.25625	0.00098	-1.2578	-0.00338	0.003125
6	-1.2578	-0.00338	-1.25625	0.00098	-1.2570	-0.001126	0.00155
7	-1.2570	-0.00113	-1.25625	0.00098	-1.2566	-6.8707	0.00075

Момент зупинки підрахунків –за величиною 8-ої графи цієї таблиці (у рядку маємо ). Як наближене значення кореня беремо число у графі 6 з рядка 7, тобто, .

3. Уточнення відокремленого кореня на інтервалі за методом пропорційних частин (методом хорд). Так як при перевірці можливості уточнення кореня за методом дихотомії було знайдено, що на інтервалі перша та друга похідні функції не змінюють знак , то до цього інтервалу можна застосувати метод хорд.

Старт. Спочатку знайдемо, який кінець хорд буде нерухомим. Згідно з теорією, буде нерухомим той кінець, для якого знак функції співпадає зі знаком другої похідної у цій точці. Так як , , то і точка є нерухомою (точніше, є нерухомою точка на хордах , які послідовно будуються у методі хорд). Тому ітераційна схема методу хорд у нашому випадку має вигляд

, (1.5.24)

Момент зупинки. Для вибору моменту зупинки в методі хорд можна скористатися загальною формулою оцінки похибки n-ого наближення (див.[9,стор.114, формула (5)]):

, (1.5.25)

де -корінь, який ми шукаємо (тобто ) і - додатна оцінка знизу абсолютної величини першої похідної функції на всьому інтервалі . Відмітимо, що ця оцінка є вірною для будь-якого ітераційного метода.

Значення одержуємо з використанням додатку TranscEq: . Якщо виконана оцінка або , то буде досягнута задана точність підрахунків. Обчислення зведемо в таблицю.

Таблиця 2.