Допоміжні матеріали до роботи NonLinSys Інструкція користувачу для роботи з програмою Newton2

Тут наведено текст програми Newton2.pas для уточнення відокремленого розв’язку системи двох нелінійних рівнянь

Вихідний файл Newton2.inp. Вихідний файл повинен бути у поточної теці (в якої розміщено тексти програми Newton2.pas і модуля Funct.pas). Структура вхідного файлу.

----------------------- початок ----------------------------

0.2 : x0 - координата x початкового наближення

0.9 : y0 - координата y початкового наближення

4 : n - число ітерацій

9 : All - число всіх позицій для друкування числа

6 : dec - число цифр після коми для друкування числа

------------------------- кінець ----------------------------

Робота з заготівкою модуля Funct.

1. Перед початком роботи потрібно підготувати записи функцій , , 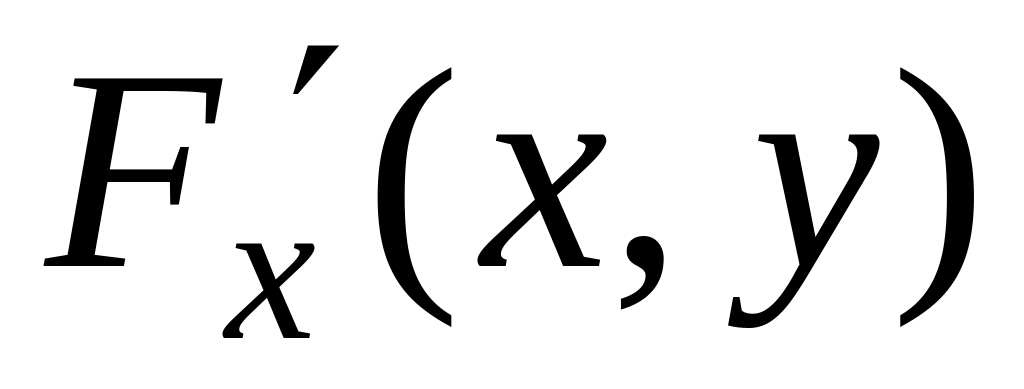і , як рядків програми на мові Turbo Pascal у вигляді функція:= вираз функцїї (див. відповідні рядкі у тексті модуля Funct);

2. Скопіювати повністю теку Newton2 (під тим же ім’ям) на власний магнітний носій (комп’ютер).

3. Завантажити Turbo Pascal, знайти в теці Newton2.pas і завантажити текст головної програми Newton2.pas у текстовий редактор Turbo Pascal.

4. Відкрити для змін вихідний текстовий файл Newton2.inp і встановити значення вхідних параметрів (кожен у окремому рядку з прогалиною після параметру, а далі до кінця рядка будь-яка послідовність символів). Наприклад:

------------------------ початок -----------------------

0.8 х₀- координата х початкового наближення,

1.5 у₀- координата у початкового наближення,

5 n - число ітерацій,

9 all- число всіх позицій для друкування числа,

8 dec- число цифр після коми для друкування числа.

------------------------------ кінець -----------------------------

5. Відкрити для зміни текстовий файл Funct.pas і замінити відповідні тіла функцій F(x,y), F_x^’(x,y), F_y^’(x,y) i G(x,y), G_x^’(x,y), G_y^’(x,y) на підготовлені раніше вирази. Скомпілювати замінений модуль.

6. Скомпілювати і виконати програму Newton2.pas.

7. Результати роботи програми будуть знаходитись у текстовому файлі Newton2.out.

Результуючий файл Newton2.out. У першому рядку наведені початкові дані (див. опис вхідного файлу). Далі йдуть рядки ітераційних кроків з номером кроку , попереднього ітераційного наближення (у дужках) плюс вектор ітераційного кроку (у дужках). Підраховане нове ітераційне наближення міститься у наступному рядку (як попереднє ітераційне наближення для наступного кроку). Наведемо приклад вихідного файлу.

---------------------- початок -----------------------------

S<Newton2>

x0= 0.800 y0= 1.500 n=5 all=9 dec=6

1:{ 0.800000 1.500000} + {-0.012964 -0.087106}

2:{ 0.787036 1.412894} + { 0.002920 -0.005103}

3:{ 0.789956 1.407791} + { 0.000025 -0.000014}

4:{ 0.789981 1.407777} + { 0.000000 -0.000000}

5:{ 0.789981 1.407777} + { 0.000000 -0.000000}

F<Newton2>

--------------------- кінець ----------------------------