Вопрос 13. Общая схема построения графика функции.

Если дана функция y=f(x), то построение графика этой функции сводится к следующим пунктам:

1) Область существования, точки разрыва, вертикальные асимптоты.

2) Участки возрастания и убывания функции, точки экстремума.

3) Участки выпуклости и вогнутости, точки перегиба

4) Наклонные асимптоты.

Замечания:

Если функция чётная, то её график симметричен относительно y (f(x)=f(-x))

Если функция нечётная, то её график симметричен относительно точки 0 (f(x)=-f(x))

Если функция является периодической, то её график достаточно строить для одного периода.

Схема исследования функций и построения графиков.

1.Общий характер функции: область определения функции и, если это возможно, область её значений; наличие чётности, периодичности; нахождение, если это возможно, пересечений графика функции с осями координат и областей её знакопостоянства (граничными точками интервалов знакопостоянства могут быть только концы интервалов области определения, точки разрыва, нули функции); область непрерывности функции, её разрывы и их характер; пределы при стремлении к границам области определения (при этом будут получены уравнения горизонтальных и вертикальных асимптот, если они есть); наличие наклонных асимптот. 2.Исследование функции с помощью первой производной на экстремумы и участки монотонности. Граничными точками интервалов монотонности функции могут быть только концы интервалов области её определения, точки разрыва, критические точки первого рода. 3.Исследование функции с помощью второй производной на выпуклость и точки перегиба. Граничными точками интервалов выпуклости графика функции могут быть только концы интервалов области её определения, точки разрыва, критические точки второго рода. После первого этапа исследования полезно построить примерный график, который уточняется в результате второго и третьего этапов.

Вопрос14 Первообразная функция. Структура множества первообразных функций

Первообразная и её свойства.

Функция F(x) называется первообразной для f(x) на интервале (a,b) если F (x) дифференцируема на (a,b) и F‘(x)=f(x).

§ Первообразная суммы равна сумме первообразных

§ Первообразная произведения константы и функции равна произведению константы и первообразной функции

§ У заданной на отрезке функции любые две первообразные отличаются на постоянную.

Определение. Функция F(x) называется первообраз­ной функцией (или просто первообр

азной) для функции f(x) на интервале (а,b), если в любой точке х интервала (a,b) функция F(x) дифференцируема и имеет про­изводную F'(x), равную f(x).

Замечание. Аналогично определяется первообразная для функции f(x) на бесконечной прямой и на открытой полу­прямой

Примеры. 1) Функция является перво-

образной для функции на интервале (—1,+1),

ибо в любой точке х этого интервала

2. Функция F(x) = sinx является первообразной для функ­ции f(x) = cos х на бесконечной прямой (—оо, оо), ибо в каждой точке х бесконечной прямой (sin x)' = cos χ.

3. Функция F(x) =lnx является первообразной для функции

f (x) = 1/x на открытой полупрямой х > 0, ибо в каждой точке x этой полупрямой

Если F(x) является первообразной для функции f(x) на ин­тервале (а,b), то, очевидно, и функция F(x) + С, где С — лю­бая постоянная, является первообразной для функции f(x) на интервале (а,b).

Естественно, возникает вопрос, как связаны между собой раз­личные первообразные для одной и той же функции f(x). Спра­ведлива следующая основная теорема.

Теорема 6.1. Если F₁{x) и F₂{x) — любые первообразные для функции f(x) на интервале (а, b), то всюду на этом интервале F₁ (х) — F₂ (х) = С, где С — некоторая постоянная.

Другими словами, две любые первообразные для одной и той же функции могут отличаться лишь на постоянную.

Доказательство. Положим Ф(х) = F₁(x)—F₂(x). Так как каждая из функций F₁ (χ) и F₂ (χ) дифференцируема на ин­тервале (a, b), то в силу теоремы 5.3 и функция Ф(х) дифферен­цируема на интервале (а,b), причем всюду на этом интервале Ф'(х) = F₁^/{x) - F₂^/(x) = f(x) - f(x) = 0.

В § 10 гл. 8 методами, не использующими результатов этой главы ¹), будет доказана теорема 8.13 следующего содержания: если функция Ф(х) дифференцируема всюду на интервале (а, Ь) и если всюду на этом интервале Ф'(х) = 0, то функция Ф(х) является постоянной на интервале (а, b).

Из этой теоремы получим, что Ф(х) = F₁(x) — F₂(x)= С = = const, что и требовалось доказать.

Следствие. Если F(x) — одна из первообразных функций для функции f(x) на интервале (а,b), то любая первооб­разная Ф(х) для функции f{x) на интервале (а,b) имеет вид Ф(х) — F(x) + С, где С — некоторая постоянная.

Функция F(x) называется первообразной для функции f(x) на интервале [a,b] (конечном или бесконечном), если в каждой точке этого интервала f(x) является производной для F(x), т.е. 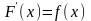. Из этого определения следует, что задача нахождения первообразной обратна задаче дифференцирования: по заданной функции f(x) требуется найти функцию F(x), производная которой равна f(x). Первообразная определена неоднозначно: для функции первообразными будут и функция arctg x, и функция arctg x-10: . Для того, чтобы описать все множество первообразных функции f(x), рассмотрим. Свойства первообразной. 1.Если функция F(x) - первообразная для функции f(x) на интервале X, то функция f(x) + C, где C - произвольная постоянная, тоже будет первообразной для f(x) на этом интервале. (Док-во: ). 2.Если функция F(x) - некоторая первообразная для функции f(x) на интервале X=(a,b), то любая другая первообразная F₁(x) может быть представлена в виде F₁(x) = F(x) + C, где C - постоянная на X функция. Док-во. Так как функции F(x) и F₁(x) - первообразные для f(x), то . 3.Для любой первообразной F(x) выполняется равенство dF(x) = f(x) dx. Из этих свойств следует, что если F(x) - некоторая первообразная функции f(x) на интервале X, то всё множество первообразных функции f(x) (т.е. функций, имеющих производную f(x) и дифференциал f(x) dx) на этом интервале описывается выражением F(x) + C, где C - произвольная постоянная.