Вопрос 1 Предел последовательности. Ограниченные, возрастающие, убывающие последовательности.

Последовательностью называется занумерованное бесконечное множество чисел, расположенных в порядке возрастания номеров (х₁, х₂, х₃…)

Формула, задающая член последовательности с номером n, называется общим членом.

Определение 1: число а называется пределом последовательности {х_n}, если члены этой последовательности становятся сколь угодно близки к числу а для всех достаточно больших номеров n.

Определение 2: число а называется пределом последовательности {х_n}, если для любого сколь угодно малого числа ε>0 найдётся N, такое, что |x_n-a|≥ε, если n≥N.

ε-окрестностью числа а называется множество точек, удовлетворяющих неравенству |х-а|≤ ε и отстоящих от а не больше, чем на ε.

Определение 3: число а называется пределом последовательности{х_n}, если для любой сколь угодно малой окрестности все члены последовательности с достаточно большими номерами попадают в эту окрестность.

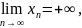если для всех достаточно больших n члены последовательности становятся положительными и сколь угодно большими.

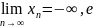сли для всех достаточно больших n члены последовательности становятся отрицательными и сколь угодно малыми.

Признаки существования предела последовательности:

1)Теорема о 2х милиционерах. {х_n}, {y_n}, {z_n} – три последовательности. х_n <y_n <z_n Тогда если 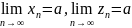, то

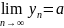
Доказательство: x_n-a≤y_n-a≤z_n-a. x_n-a и z_n-a стремятся к 0, значит, и y_n-a→0

2) Если последовательность {х_n} является возрастающей и ограниченной сверху, то она имеет конечный предел.

Последовательность {х_n} называется возрастающей, если х₁≤х₂≤х₃≤ х_n

Аналогично – убывающая.

Последовательность {х_n} называется ограниченной сверху, если существует такое число М, что x_n≤M для всех номеров n.

Аналогично – ограниченная снизу.

Свойства пределов последовательности. Признаки сходимости.

1) Если {х_n} имеет конечный предел а, то она ограничена.

Док-во: пусть ε>0. т.к. точка а является пределом, то все члены последовательности, начиная с некоторого номера, попадают в ε-окрестность этой точки. Вне этой окрестности может быть только конечное число членов последовательности. А значит, существует отрезок [-M;M], содержащий все члены нашей последовательности, следовательно, последовательность ограничена.

2) Пусть

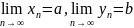
Тогда

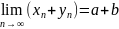
Док-во: т.к. члены последовательности 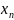сколь угодно близки к а для достаточно больших n, а члены последовательности y_n сколь угодно близки к b для достаточно больших n, то очевидно, что члены последовательности x_n+y_n сколь угодно близки к а+b для всех достаточно больших n.

3) Если , то

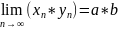
4) Если и b≠0, то

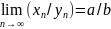
Вопрос 2 Предел функции.

Пусть функция y=f(x) определена на некотором промежутке, содержащем точку a, всюду, кроме, может быть, самой этой точки a.

Определение 1: число A называется пределом функции y=f(x) в точке a, если значения функции f(x) сколь угодно близки к числу A для всех значений x, достаточно близких к точке a.

Определение 2: число A является пределом функции y=f(x) в точке a, если для любого ε>0 найдётся Δ>0 такое, что для 0<|x-a|<Δ выполняется |f(x)-a|< ε.

Определение 3: число A является пределом функции y=f(x) в точке a, если |f(x)-A|< ε для x, лежащих в достаточно малой Δ-окрестности точки a.

Свойства пределов функции.

Будем говорить, что функция y=f(x) ограничена в некоторой окрестности точки x=a, если существует такое M>0, что в этой окрестности |f(x)| не превосходит M.

Свойства:

1) Если функция y=f(x) имеет в точке a предел, равный A, тогда функция y=f(x) ограничена в некоторой окрестности точки a.

Если f(x)→A при x→a, то |f(x)-A|≤ ε в некоторой окрестности точка a, но тогда по свойству модуля |f(x)|-|A|<|f(x)-A| => |f(x)|≤|f(x)-A|, т.е., f(x) ограничена.

2) Если f(x)→A при x→a, а g(x)→B при x→a, то предел (f(x)+g(x)) при x→a равен A+B.

3) Если 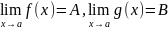, то предел произведения равен произведению пределов.

4) Если и B≠0, то частное пределов равно пределу частного.

5) Если в окрестности точки a f(x)≥0 и существует 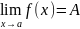, то A≥0.

Док-во – методом от противного: если A<0, то, поскольку значения f(x) должны быть сколь угодно близки к A, они тоже будут <0, что противоречит условию.

6) Если в некоторой окрестности точки a f(x)≤g(x) и , то A≤B.

Док-во: пусть h(x)=g(x)-f(x). 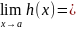B-A,

следовательно, B-A≥0, следовательно, B≥A.

7) Теорема о двух милиционерах.

Если в некоторой окрестности точки a f(x)≤h(x)≤g(x) и если 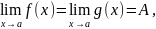то