Вопрос22. Интегрирование тригонометрических выражений.

Интеграл вида . Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx. Интегралы этого вида вычисляются с помощью подстановки t=tg(x/2). Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную. ,  Тогда  Таким образом: Описанное выше преобразование называется универсальной тригонометрической подстановкой.

  Пример.

  Несомненным достоинством этой подстановки является то, что с ее помощью всегда можно преобразовать тригонометрическую функцию в рациональную и вычислить соответствующий интеграл. К недостаткам можно отнести то, что при преобразовании может получиться достаточно сложная рациональная функция, интегрирование которой займет много времени и сил.

 Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.

Интеграл вида  если функция R является нечетной относительно cosx.

 Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.

 

Функция  может содержать cosx только в четных степенях, а следовательно, может быть преобразована в рациональную функцию относительно sinx.

Вообще говоря, для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.

Интеграл вида  если функция R является нечетной относительно sinx.

 По аналогии с рассмотренным выше случаем делается подстановка t = cosx.

Тогда

Интеграл вида функция R четная относительно sinx и cosx.

 

  Для преобразования функции R в рациональную используется подстановка

t = tgx. Тогда

 Интеграл произведения синусов и косинусов различных аргументов.

В зависимости от типа произведения применятся одна из трех формул:

Вопрос 23. Определенный интеграл. Необходимое условие интегрируемости.

Пусть функция задана на отрезке . Рассмотрим разбиение R отрезка точками:

R: . Обозначим

— параметр разбиения. Точка — произвольная.

Составим сумму (интегральная сумма):

Если , не зависящий от разбиения R и выбора , то говорят, что определен интеграл Римана: . Т.е. .

Если (существует и конечен), то функция называется интегрируемой

Определение . Функция f(x) называется интегрируемой на сегменте [a,b] если существует конечный предел I интегральных сумм этой функции при d стремящихся к 0. Указанный предел I называется определенным интегралом от функции f(x) по сегменту [a,b] и обозначается следующим образом

I =

Понятие верхней и нижней сумм. Пусть функция f(x) ограничена на сегменте [а,b] и Т — разбиение этого сегмента точками Обозначим через M_i и m_i

соответственно точную верхнюю и точную нижнюю грани этой функции на сегменте . Суммы

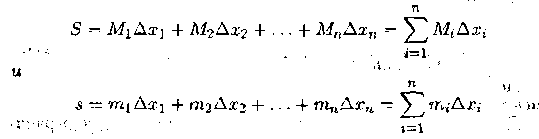
называются соответственно верхней и нижней сум­мами функции f(x) для данного разбиения Т сегмента [а, Ь].

Очевидно, что любая интегральная сумма данного

разбиения Т сегмента [а,b] заключена между верхней и ниж­ней суммами S и s этого разбиения.

Свойства верхних и нижних сумм. Докажем справед­ливость следующих свойств верхних и нижних сумм:

1°. Для любого фиксированного разбиения Т и для любого ε > 0 промежуточные точки на сегментах можно

выбрать так, что интегральная сумма будет удовле-

творять неравенствам . Точки можно

выбрать также и таким образом, что интегральная сумма будет удовлетворять неравенствам

Пусть Т — некоторое фиксированное разбиение сегмента [а, 6]. Докажем, например, возможность выбора по данному ε > 0 то­чек так, что будет выполняться неравенство < е. По определению точной грани Mi для данного ε > 0 на сегменте можно указать такую точку , что

Умножая эти неравенства на и затем складывая, получим

Справедливость свойства 1° установлена.

2°. Если разбиение Т' сегмента [а,b] получено путем добав­ления новых точек к точкам разбиения Т этого сегмента, то верхняя сумма S' разбиения Т' не больше верхней суммы S раз­биения Т, а нижняя сумма s' разбиения Т' не меньше нижней суммы s разбиения Т, т. е.

Так как разбиение Т' может быть получено из разбиения Г пу­тем последовательного добавления к последнему новых точек, то, очевидно, сформулированное свойство достаточно доказать для случая, когда к разбиению Т добавляется одна точка. Пусть эта точка х' располагается на сегменте разбиения Т сегмента [а,b]. Обозначим через точные верхние грани

функции f(x) на сегментах , через

длины этих сегментов и через S и S' верхние суммы разбие­ния Г и разбиения Т', полученного добавлением к разбиению Т точки х'. Отметим, что . Кроме того, если Mi — точная верхняя грань значений функции f(x) на сегмен­те , поскольку очевидно, что точная верхняя грань функции на части сегмента не превосходит точную верхнюю грань Mi этой функции на всем сегменте . Поэтому, учитывая, что суммы S и 5" раз­личаются лишь слагаемыми , получим

т. е. Доказательство для нижних сумм проводится аналогично.

3°. Пусть Т' и Т" — любые два разбиения сегмента [а, b]. Тогда нижняя сумма одного из этих разбиений не превосходит верхнюю сумму другого. Именно, если s', S' и s", S" — соот­ветственно нижние и верхние суммы разбиений Т' и Т", то

Выше мы установили, что нижняя сумма данного разбиения не превосходит верхнюю сумму этого разбиения. Пусть Т — разби­ение сегмента [a, b], полученное объединением разбиений ¹) Т' и Г", a s и S — верхняя и нижняя суммы разбиения Т. Так как разбиение Т может быть получено из разбиения Т' добавлением к нему точек разбиения Г", то по свойству 2° и отмеченному свойству нижней и верхней суммы одного и того же разбиения имеем

Но разбиение Т может быть также получено из разбиения Т" добавлением к нему точек разбиения Т'. Поэтому

Сравнивая установленные выше неравенства с только что полу­ченными, убедимся, что

4°. Множество {S} верхних сумм данной функции f(x) для всевозможных разбиений сегмента [α, b] ограничено снизу. Множество {s} нижних сумм ограничено сверху.