Вопрос 9.Правило Лопиталя.

Пусть выполнены следующие условия:

1. Функции f(x) и g(x) определены и дифференцируемы в выколотой окрестности точки a.

2. (1)

3. g(x) и f(x) не равны нулю в этой выколотой окрестности.

Если при этом существует (2)

То существует и (3)

П ричем, они равны между собой.(4)

Д оказательство: Доопределим функции f(x) и g(x) в точке x=a, положив f(a)=g(a)=0. Рассмотрим отрезок между числами a и x, где точка из упомянутой в условии выколотой окрестности. Для определенности будем считать, что x<a. Обе функции на отрезке [x,a] неперывны, а в интервале (x,a) дифференцируемы, т.е. удовлетворяют условиям теоремы Коши. Следовательно, Существует такая точка с(x,a), что выполняется равенство(5)

Так как f(a)=g(a)=0. При ха будет са, потому x<c<a.

П о условию теоремы существует (2). Здесь х можно заменить любой другой буквой, в частности с. Переходя к пределу в равенстве (5) при ха, получим

Или, что то же самое (4).

Правило Лопиталя

Случай 1. Неопределённость 0/0

Теорема.

Пусть функции y=f(x) и y=g(x) дифференцируемы в некоторой окрестности точки а. Пусть f(a)=0 и g(a)=0. Тогда =

Док-во:

Применим т.Коши к отрезку [a,x].

Тогда 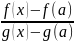= , где a<c<x

(т.к. f(a)=0; g(a)=0)

Пусть х→а. Тогда с→а

= =

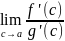Случай 2. Неопределённость ∞/∞

Теорема.

Пусть функции y=f(x) и y=g(x) дифференцируемы в некоторой окрестности точки а кроме самой точки а. Пусть

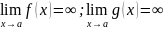Тогда

=

Вопрос 10. Возрастание и убывание функции.

Функция y=f(x) называется возрастающей на некотором промежутке, если для двух точке x₁ и x₂ этого промежутка из условия x₁<x₂ следует

f(x₁)<f(x₂)

Теорема о возрастании:

Часть первая. Мы учим летать самолёты.

Если функция y=f(x) на некотором промежутке является возрастающей, то на этом промежутке f’(x)≥0

Часть вторая. Москва слезам не верит.

Если на некотором промежутке f’(x)>0, то функция y=f(x) является на этом промежутке возрастающей.

Доказательство первой части!

Пусть x – некоторая точка. Дадим приращение х+Δх.

Тогда приращение функции Δу=f(х+Δх)-f(x).

Δу=f(х+Δх)-f(x)>0, если Δх>0

Δу=f(х+Δх)-f(x)<0, если Δх<0

Поэтому всегда >0 Значит, y’=f’(x)= ≥0

Доказательство второй части! Внимание, товарищи!

Возьмём произвольные точки x₁ и x₂ из нашего промежутка, такие, что x₁<x₂. Запишем для таких точек формулу конечных приращений.

f(x₂)-f(x₁)=f’( )(x₂-x₁) => f(x₂)>f(x₁), т.е., функция является возрастающей.

Теорема об убывающей функции.

1) Если y=f(x) является убывающей на некотором промежутке, то на этом промежутке f’(x)≤0.

2) Если f’(x) на некотором промежутке ≤0, то f(x) на этом промежутке является убывающей. Док-во аналогично предыдущему.

ВОЗРАСТАНИЕ И УБЫВАНИЕ Ф-ИИ.

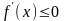Условие (нестрогой) монотонности функции на интервале. Пусть функция имеет производную в каждой точке интервала (a,b). Для того, чтобы эта функция была монотонно возрастающей на интервале (a,b), необходимо и достаточно выполнение условия для . Для того, чтобы функция была монотонно убывающей на интервале , необходимо и достаточно выполнение условия для .

Док-во. Необходимость. Если f(x) монотонно возрастает, то для любых , при выполняется .

Достаточность. Пусть для , 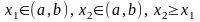. По формуле конечных приращений Лагранжа , т.е. монотонно возрастает на (a,b).

Случай монотонного убывания рассматривается аналогично.

В случае, рассмотренном в Теор.8.2.1, мы не исключаем для функции f(x) возможность оставаться постоянной на некотором подынтервале ( и, как следствие, для её производной быть равной нулю на этом подынтервале). Если эту возможность исключить, получим условия строгой монотонности функции на интервале:

Условие строгого возрастания функции на интервале. Пусть функция имеет производную в каждой точке интервала (a,b). Для того, чтобы эта функция строго возрастала на интервале (a,b), необходимо и достаточно, чтобы выполнялись условия:

1. для ;

2. не обращается тождественно в нуль ни на каком подынтервале этого интервала.

Док-во. Необходимость. Если f(x) строго возрастает, то, по теор.8.2.1 для ; при этом не обращается в нуль ни на каком подынтервале этого интервала, так как в этом случае по теор.8.1 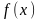была бы постоянной на этом подынтервале, что противоречит условию строгого возрастания.

Достаточность. Если выполняются условия теоремы, то, по теор.8.2.1, f(x) не убывает. Предположим, что для двух точек и интервала (a,b) значения функции равны: . Тогда, вследствие неубывания f(x), для , т.е. постоянна на на этом интервале, что противоречит второму условию теоремы. Случай строгого убывания рассматривается аналогично.