Вопрос 31. Дифференциальные уравнения с разделенными переменными

Рассмотрим дифференциальное уравнение вида: f1(x)dx=f2(y)dy,     (1) которое называется  уравнением с разделенными переменными. Пусть найдено некоторое его решение y(x). При подстановке y=y(x) в дифференциальное уравнение (1) оно обратится в тождество и, интегрируя его, имеем f1(x)dx=∫f2(y)dy+C,    (2)  где C - произвольная постоянная. Получили уравнение (2), которому удовлетворяют решения дифференциального уравнения (1). Обратно, каждое решение y(x) уравнения (2) является и решением исходного дифференциального уравнения (1), так как если y(x) обращает в тождество уравнение (2), то, дифференцируя это тождество, получим, что y(x) обращает в тождество и уравнение (1). Следовательно, равенство (2) содержит все решения дифференциального уравнения (1) и оно называется общим интегралом уравнения (1). Из него при определенных условиях можно выразить y от x или x от y. Если надо выделить частное решение, удовлетворяющее условиям: y=y0 при x=x0, то таким решением является равенство ∫xx0f1(t)dt=∫yy0f2(t)dt, так как оно содержится в общем интеграле (2) и удовлетворяет начальным условиям.

Пример. Найти решение дифференциального уравнения xdx+ydy=0. Решение. Переменные здесь разделены, то есть коэффициенты при дифференциалах dx и dy являются соответственно функциями только от x и y, следовательно, интегралом уравнения будет ∫xdx+∫ydy=C1 или 2x2+2y2=C1 или x2+y2=2C1. Ответ. x2+y2=C2, C -- произвольная постоянная.

Вопрос 32. Диф. Уравнения с разделяющимися пер-ми.

Определение. Дифференциальное уравнение называется уравнением с разделяющимися переменными, если его можно записать в виде

Такое уравнение можно представить также в виде:

Перейдем к новым обозначениям

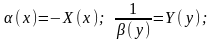
Получаем:

После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными. Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение. Пример. Найти общее решение дифференциального уравнения:

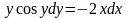
Интеграл, стоящий в левой части, берется по частям (см. Интегрирование по частям.):

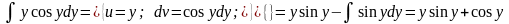
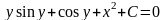
• это есть общий интеграл исходного дифференциального уравнения, т.к. искомая функция и не выражена через независимую переменную. В этом и заключается отличие общего (частного) интеграла от общего (частного) решения. Чтобы проверить правильность полученного ответа продифференцируем его по переменной х.

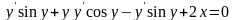
- верно

Вопрос 33. Диф. Однородные диф. Ур-я 1-го порядка.

Ур-е 1-го порядка y’= f(x,y) (1) однородно если f(ax,ay)=af(x,y) (2).

Ур-е n-го порядка однородно если f(ax,ay)=a^nf(x,y).

Если ф-я f(x,y) удолетворяет условию (2) то можно записать x<>0 f(x,y)= f(x*1,x*y/x)= f(1,y/x) = =g(y/x) f(x,y)=g(y/x) f(1,u)=g(u) (3). В силу соотношения (3) ур-е (2) имеет вид y’=g(y/x) (4). Это ур-у не явл. ур-м с разд. пер. но может быть сведено к нему заменой u=y/x (5): y=ux y’=u’x+u подставим в (4) u’x+u=g(u) xdu/dx=g(u)-u du/(g(u)-u)=dx/x (6) проинтегр.(6) g(u)-u<>0

du/(g(u)-u)=ln|x|+c (7) Соотношение (7) задает общий интеграл для ур-я (4) после этого возвр. к x, y. Выпис. ур-е g(u)-u=0 (8) и реш-т, корень ур-я (8) задает реш-е ур-я (1).