
- •Вопрос 1 Предел последовательности. Ограниченные, возрастающие, убывающие последовательности.
- •Вопрос 2 Предел функции.
- •Вопрос 3. Замечательные пределы.
- •Вопрос 4. Непрерывные функции
- •Вопрос 5 .Определение производной. Примеры.
- •Вопрос 6. Таблица производных.
- •Вопрос 7. Основные правила дифференцирования.
- •Вопрос 8. Производные и дифференциалы высших порядков.
- •Вопрос 9.Правило Лопиталя.
- •Вопрос 10. Возрастание и убывание функции.
- •Вопрос11 Точки экстремума функции. Необходимые условия экстремума.
- •Вопрос 12. Выпуклость и вогнутость.
- •Вопрос 13. Общая схема построения графика функции.
- •Вопрос14 Первообразная функция. Структура множества первообразных функций
- •Вопрос 15. Неопределенный интеграл его свойства. Таблица интегралов
- •Вопрос 16. Замена переменной в неопределенном интеграле.Примеры.
- •Вопрос 17. Интегрирование по частям в неопределенном интеграле. Примеры
- •Вопрос 18. Вычислениe неопределённых интегралов, содержащих в знаменателе квадратный трёхчлен.
- •Вопрос 19. Итегрирование рациональных дробей
- •Вопрос 20. Разложение рациональной дроби на простейшие.
- •Вопрос21 Интегрирование иррациональных выраж. Дробно- линейные иррациональности.
- •Вопрос22. Интегрирование тригонометрических выражений.
- •Вопрос 23. Определенный интеграл. Необходимое условие интегрируемости.
- •Вопрос 24. Определение и геометрический смысл определенного интеграла
- •Вопрос25 Свойства определенного интеграла
- •Вопрос 26. Приложение определенного интеграла. Вычисление площади криволинейной трапеции.
- •Вопрос 27. Теорема о замене переменной в определенном интеграле.
- •Вопрос 28. Несобственные интегралы.
- •Вопрос 29. Понятие диф ур-я, основные определения.
- •Вопрос 30, Задача Коши для диф. Ур 1пор.
- •Вопрос 31. Дифференциальные уравнения с разделенными переменными
- •Вопрос 32. Диф. Уравнения с разделяющимися пер-ми.
- •Вопрос 33. Диф. Однородные диф. Ур-я 1-го порядка.
- •Вопрос34. Лин диф ур.
- •Вопрос 36.Интегрируемые типы диф ур-й 2-го порядка
- •Вопрос 37. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
- •Вопрос 38. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида.
- •Вопрос 39. Комплексные числа.
- •Вопрос 40. Функции нескольких переменных. Основные определения и свойства.
- •Вопрос 41. Производные от функций многих переменных.
- •Вопрос 42. Исследование функций двух независимых переменных на экстремум
- •Вопрос 43. . Числовые ряды. Основные понятия.
- •Вопрос 44. Признак сравнения.
- •Вопрос 45. Знакочеред ряды. Т Лейбница.
- •Теор Признак Лейбница
- •Вопрос 47. Разложение элементарных функций в ряд Маклорена
- •Вопрос 48. Интегрирование дифференциальных уравнений с помощью степенных рядов.
- •Вопрос 49. Решение дифференциальных уравнений с помощью степенных рядов.
- •Вопрос 50. Множества. Операции над множествами
Вопрос 24. Определение и геометрический смысл определенного интеграла
Пусть
на отрезке
 задана функция
.
Разобьём отрезок
произвольным образом на n
частей точками
задана функция
.
Разобьём отрезок
произвольным образом на n
частей точками
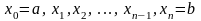 ;
длину
;
длину
 -го
отрезка обозначим
-го
отрезка обозначим
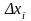 :
:
 ;
максимальную из длин отрезков обозначим
;
максимальную из длин отрезков обозначим
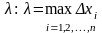 .
На каждом из отрезков
.
На каждом из отрезков
 выберем произвольную точку
выберем произвольную точку
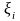 и составим сумму
и составим сумму

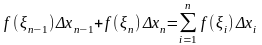 .
.
Сумма
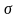 называется интегральной суммой. Если
существует (конечный) предел
последовательности интегральных сумм
при
называется интегральной суммой. Если
существует (конечный) предел
последовательности интегральных сумм
при
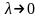 ,
не зависящий ни от способа разбиения
отрезка
на части
,
не зависящий ни от способа разбиения
отрезка
на части
 ,
ни от выбора точек
,
то функция
называется интегрируемой по отрезку
,
а этот предел называется определённым
интегралом от функции
по отрезку
и обозначается
,
ни от выбора точек
,
то функция
называется интегрируемой по отрезку
,
а этот предел называется определённым
интегралом от функции
по отрезку
и обозначается
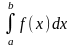 .
.
Геометрический
смысл определённого интеграла.
если
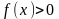 на отрезке [a,b],
то
равен площади криволинейной трапеции
ABCD,
ограниченной снизу отрезком [a,b],
слева и справа - прямыми x=a
и x=b,
сверху - функцией
.
на отрезке [a,b],
то
равен площади криволинейной трапеции
ABCD,
ограниченной снизу отрезком [a,b],
слева и справа - прямыми x=a
и x=b,
сверху - функцией
.
Если положение точки при её движении по числовой прямой задаётся функцией S = f(t), где t – время движения, то производная функции S – мгновенная скорость движения в момент времени t. По аналогии с этой моделью вообще говорят о том, что производная функции у = f(x) – скорость изменения функции в точке х.
Вопрос25 Свойства определенного интеграла
Линейность.

Док-во. Рассмотрим разбиение R отрезка точками:
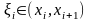 — произвольная
точка;
.
Составим интегральную сумму для левой
части равенства:
— произвольная
точка;
.
Составим интегральную сумму для левой
части равенства:

переходя
к пределу при
 получим
требуемое равенство.
получим
требуемое равенство.
Аддитивность по множеству
Если
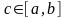 и
интегрируема на
и
интегрируема на
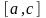 и
и
 ,
то
интегрируема на
и
,
то
интегрируема на
и
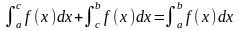
Док-во.
Рассмотрим разбиение
 ;
;

Обозначим
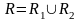 :
:
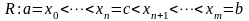
Если
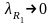 и
и
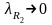 ,
то
,
то
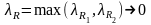
Составим
интегральную сумму:
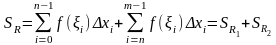
Прейдем
к пределу при
и
:
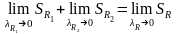
Т.е. получим требуемое равенство.
Свойства определённого интеграла.
1) ;
2)
;
2)
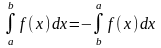 ;
3)
;
3)
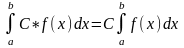 ;
4)
;
4)
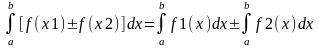 ;
5)
;
5)
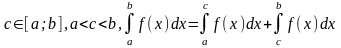 .
.
Формула Ньютона-Лейбница
Если
непрерывна на
,
а
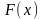 ее
первообразная, то:
ее
первообразная, то:
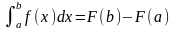 .
.
Док-во.
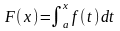 — непрерывная функция
— непрерывная функция
 .
Рассмотрим разность
.
Рассмотрим разность
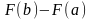 .
.
Разобьем отрезок на части точками R:
Представим
разность
в виде:
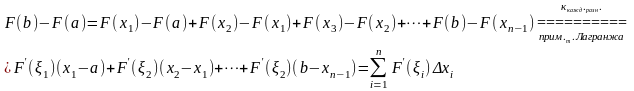
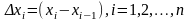 .
Но
.
Но
 ,
поэтому
,
поэтому
 .
.
Переходим
к пределу при
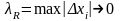 ,
получим
.
,
получим
.
Cв-ва опр. интеграла:
(все интегралы на отрезке от А до В)
1 ∫С·f(x)dx=C·∫f(x)dx
2 ∫(f(x)±g(x))dx=∫f(x)dx±∫g(x)dx
3 ∫f(x)dx=-∫f(x)dx
4 Если f(x)≤g(x) на (A,B), то ∫f(x)dx≤∫g(x)dx
5 Если на (А,В) m=minf(x) M=maxf(x)то m(B-
-A)≤∫f(x)dx≤M(B-A)
6 Если f(x) непрерывна на (A,B) то сущ. также точка
С∈(A;B) ∫f(x)dx=f(C)·(B-A)
7 Если f(x) непрерывна на (А,В) то ∫f(x)dx существует
8 ∫f(x)dx=∫(a→d)f(x)dx+∫(d→b)f(x)dx
9 Формула Ньютона-Лейбница:
∫f(x)dx=F(B)-F(A)→F`(x)=f(x)
Вопрос 26. Приложение определенного интеграла. Вычисление площади криволинейной трапеции.
1)
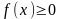
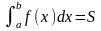
Площадь криволинейной трапеции с оси X=a, X=b и боковыми сторонами: отрезок и график функции .
2)
Площадь четырехугольника заключенного
между кривыми
 ,
,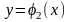 ;
;
 и прямыми X=a,
X=b
и прямыми X=a,
X=b
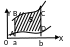
 — разность площадей двух трапеций
— разность площадей двух трапеций
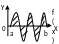
Можно находить площади более сложных фигур: — меняет знак S — сумма четырех площадей
Вычисление объема тела вращения.
Пусть кривая заданная на отрезке , вращается вокруг оси OX.
Требуется найти объем тела вращения

Разобьем отрезок на части точками:
Обозначим
Проведем
через точки
 плоскости
плоскости
 .
.
Тело
вращения разобьется на цилиндры с
объемом
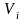
высотой
,
радиусом оси
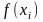 .
.
Объем
цилиндра
 .
Объем вписанного ступенчатого
цилиндрического тела
.
Объем вписанного ступенчатого
цилиндрического тела
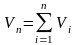 .
.
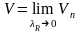 — объем
тела вращения вокруг оси OX.
Здесь
— объем
тела вращения вокруг оси OX.
Здесь

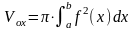 ;
;
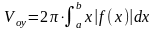
Объёмы тел вращения.
Вычисление
объёма тела по площадям поперечных
сечений.
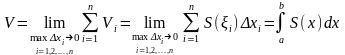
Объём
тела, получающегося при вращении кривой
вокруг координатной оси
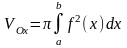
Объём
тела, получающийся при вращении сектора,
ограниченного кривой
 и двумя полярными радиусами
и двумя полярными радиусами
 и
и
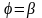 ,
вокруг полярной оси находится
по формуле
,
вокруг полярной оси находится
по формуле
 .
.
Вычисление
работы с помощью определённого интеграла.
1) Если сила постоянна
![]() ,
то работа выражается следующим образом
,
то работа выражается следующим образом
![]() .
2) Если сила переменная
величина, то
.
2) Если сила переменная
величина, то
![]() .
.
Путь,
пройденный телом
![]()
