Тема 3. Единая геометрия ри

Несмотря на большое разнообразие отдельных видов РИ, все они имеют режущий клин, ограниченный передней А и задней А поверхностями (рис. 1.1,а, с. 2).

Работоспособность лезвия в значительно степени определяется его геометрическими параметрами: передним углом , задним главным и вспомогательным углами , главным и вспомогательным углами в плане, углом наклона главной режущей кромки (РК) (рис. 1.3, а, с.2).

Однако для изготовления и контроля РИ часто необходимо знать геометрические параметры лезвия в сечениях, перпендикулярных и параллельных основным базовым поверхностям РИ (например, для токарного резца на рис. 1.4, с.3 такими сечениями являются продольное сечение I-I и поперечное сечение II-II).

Пусть для этого токарного резца известны углы l, и углы в главной секущей плоскости Р : , g. Необходимо определить угол a_I в сечении I-I и угол a_II в сечении II-II.

Введём дополнительный угол w- угол между проекцией главной РК АВ на основную плоскость и следом CD главной задней поверхности резца на основной плоскости.

В некоторой произвольно взятой точке М главной РК образуются задние углы между главной задней поверхностью и инструментальной плоскостью резания, которая проходит через перпендикуляр МЕ и РК АВ: в главной секущей плоскости

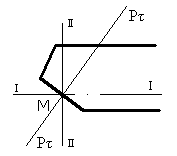
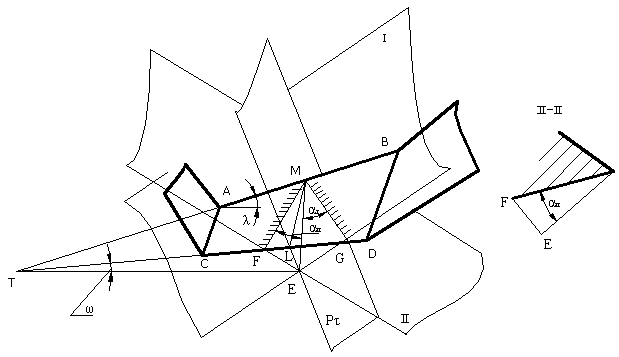
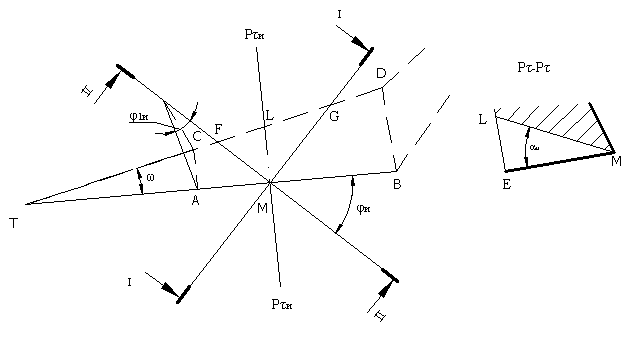
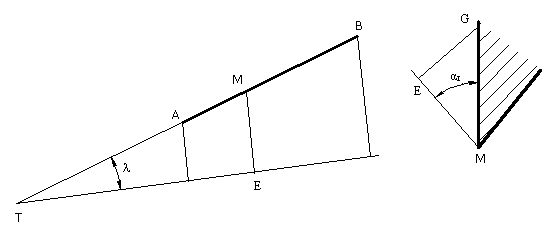Рис. 9

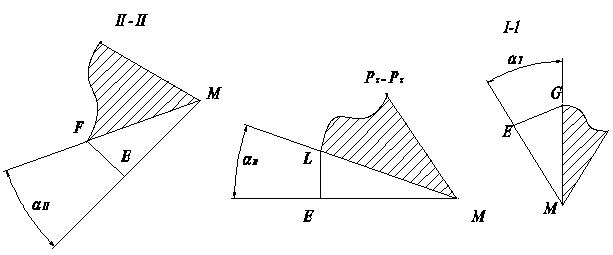
Рис. 10

Р угол ЕML равен углу ; в сечении I-I - угол EMG = a_I ; в сечении II-II - угол EMF = a_II.

Все секущие плоскости проходят через общий перпендикуляр к основной плоскости МЕ, который является общим катетом трёх прямоугольников, лежащих в указанных выше секущих плоскостях.

Расстояние от точки М до основной плоскости:

ЕМ = EL / tg a_и = EG / tg a₁ = EF / a_II.

Из треугольника TEL (на виде сверху это треугольник TML)

tg w = EL / ET =(EM * tg a_и) / (EM / tgl) = tg a_{и *} tgl . (1)

Из треугольника EFL и треугольника EGL (по теореме синусов с использованием формул приведения).<FLM = 90-ω.

sinLFM/ sinFLM = EL / EF = sin (w + j_и) / cosw;

EL / EG = cos (w + j_и)/cosw.

Для в сечении I-I:

ctg a₁ = EM / EG =(EL /tg a_и) / (EL * cos w / cos (w +j_и)) =

(cos (w +j_и)/ cos w ) * ctg a_и; (2)

Для в сечении II-II:

ctg a_1I = EM / EF =(EL /tg a_и) / (EL * cos w / sin (w +j_и)) =

(sin (w +j_и)/ cos w ) * ctg a_и. (3)

После преобразования и подстановки tg a_и = tg w / tg l получим:

ctg a_I = ctg a_{и *} cos j_и – tg l * sin j_{и ;} (4)

ctg a_II = ctg a_{и *} sin j_и – tg l _* cos j_{и .} (5)

Умножив ур-е (4) на cos j_и и ур-е (5) на sin j_и , получим два уравнени, из совместного решение которых относительно ctg j_и имеем:

ctg a_И = ctg a_{I *} cos j_и + ctg a_{II *} sin j_{и .} (6)

Аналогично рассуждая для углов на передней поверхности резца, получим следующие формулы для передних углов g_I, g_II и g_И:

tg g_I = tg g_{I *} cos j_и - tg l _* sin j_{и ;} (7)

tg g_II = tg g_{И *} sin j_и + tg l _* cos j_и; (8)

tg g_И = tg g_{I *} cos j_и + tg g_{II *} sin j_и. (9)

Решив систему уравнений (4) и (5) относительно tg l получим:

tg l= сtg a_{II *} cos j_и – сtg a_{I *} sin j_{и .} (10)

Решая систему уравнений (7) и (8) относительно tg l получим:

tg l= tg g_{II *} cos j_и – tg g_{I *} sin j_и . (11)

Полученные формулы (1) – (11) называются формулами единой геометрии РИ, т.к. они справедливы для всех РИ содержащих лезвие.