
- •1. Физические модели в механике. Тело отсчета. Система отсчета. Операции с векторами. Время. Траектория. Путь. Перемещение.
- •2. Скорость и ускорение. Нормальное и касательное ускорение.
- •3. Угловые характеристики: перемещение (поворот), скорость и ускорение. Связь между линейными и угловыми кинематическими характеристиками.
- •5. Преобразования координат г. Галилея. Принцип относительности г. Галилея.
- •6. Сила тяжести и вес тела. Закон Гука. Модули упругости, коэффициент Пуассона.
- •7. Сухое и вязкое трение. Формула Ньютона. Виды сухого трения: покоя, скольжения, качения.
- •8. Закон Всемирного тяготения. Напряженность, работа, потенциал гравитационного поля.
- •9. Космические скорости.
- •10. Неинерциальные системы отсчета. Сила инерции. Сила Кориолиса и ее проявление в природе и технике.
- •11. Импульс. Вывод закона сохранения импульса из второго закона динамики. Центр масс системы материальных точек.
- •12. Физические основы космических полетов: законы движения тел переменной массы.
- •13. Энергия как количественная мера движения материи. Работа силы. Мощность. Кинетическая энергия и ее связь с работой.
- •14. Потенциальная энергия. Потенциальное поле. Консервативные силы. Работа в поле потенциальных сил.
- •Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.
- •16. Момент инерции и момент импульса. Уравнение моментов. Основное уравнение динамики вращательного движения.
- •17. Момент инерции твердого тела относительно неподвижной оси вращения. Теорема Штейнера. Моменты инерции тел вращения.
- •18. Кинетическая энергия твердого тела.
- •19. Постулаты Эйнштейна. Преобразования Лоренца. Инварианты преобразований.
- •20. Элементы релятивистской динамики: масса, импульс и энергия. Релятивистская динамика Энергия и импульс
- •[Править]Уравнения движения
- •21. Общие свойства жидкостей и газов. Давление. Закон Паскаля, закон Архимеда. Равновесие, погруженных в жидкость, тел. Идеальная жидкость.
- •Характерные свойства газов, жидкостей и твердых тел.
- •22. Уравнение неразрывности струи. Уравнение Бернулли. Течение вязкой жидкости. Уравнение неразрывности.
- •Уравнение Бернулли.
- •23. Ламинарное и турбулентное течение. Число Рейнольдса. Движение вязкой жидкости в трубе. Формула Пуазейля. Метод Стокса.
- •25. Сложение гармонических колебаний: колебаний одного направления, взаимно перпендикулярных колебаний.
- •§2.1. Сложение гармонических колебаний одного направления.
- •§2.2. Сложение взаимно перпендикулярных колебаний.
- •26. Маятники: физический, математический и пружинный.
- •27. Свободные колебания. Коэффициент затухания, декремент затухания, добротность колебательной системы.
- •28. Вынужденные колебания. Резонанс.
- •29. Понятие волны. Продольные и поперечные волны. Волновое уравнение. Энергия бегущей волны. Вектор Умова. Стоячие волны.
- •Волновое уравнение.
- •Вектор Умова.
- •Стоячие волны.
- •30. Уравнение состояния. Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам.
- •31. Классическая теория теплоемкости идеального газа.
- •33. Политропические процессы. Политропные процессы
- •34. Обратимые и необратимые тепловые процессы. Тепловые двигатели. Обратимые и необратимые тепловые процессы.
- •35. Второе начало термодинамики в формулировке Томсона и Клаузиуса. Цикл Карно. Кпд тепловой машины.
- •36. Энтропия. Закон возрастания энтропии. Цикл Карно в (t,s) – координатах.
- •1. Понятии и общая характеристика энтропии
- •2. Принцип возрастания энтропии
- •37. Термодинамические потенциалы.
- •38. Реальные газы. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса.
- •Отступление от законов идеального газа. Уравнение Ван-дер-Ваальса.
- •3. Изотермы Ван дер Ваальса и их анализ.
- •39. Внутренняя энергия реального газа. Эффект Джоуля-Томсона. Энтальпия.
- •Внутренняя энергия реального газа.
- •Эффект Джоуля—Томсона.
- •40. Свойства жидкостей. Поверхностное натяжение. Явление смачивания.
- •41. Давление под искривленной поверхностью жидкости. Капиллярные явления.
- •42. Свойства твердых тел. Моно- и поликристаллы. Типы кристаллических решеток.
- •43.Дефекты в кристаллах. Теплоемкость твердого тела.
- •44. Фазовые переходы первого рода. Условия равновесия фаз. Диаграмма фазового равновесия. Тройная точка. Фазовые переходы второго рода. Λ-переходы. Фазовые переходы первого рода
- •Примеры фазовых переходов первого рода
- •3.1. Условия равновесия фаз. Фазовые диаграммы
10. Неинерциальные системы отсчета. Сила инерции. Сила Кориолиса и ее проявление в природе и технике.
Неинерциальные системы отсчета (НИСО). Уравнение движения материальной точки в НИСО.
Различают
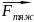 ,
,
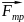 ,
,
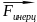 .
В СО связанные с Землей, на каждое тело
действует
:
.
В СО связанные с Землей, на каждое тело
действует
:
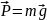 – весом называют силу, с кот любое тело
в поле сил тяжести, созданным небесным
объектом, действует на опору или подвес,
кот препятствует свободному падению
тел. Отметим, что сила тяж и веса приложены
к разным объектам: вес – к опоре,
– весом называют силу, с кот любое тело
в поле сил тяжести, созданным небесным
объектом, действует на опору или подвес,
кот препятствует свободному падению
тел. Отметим, что сила тяж и веса приложены
к разным объектам: вес – к опоре,
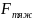 – к телу. Эти силы имеют различную
физическую природу: вес – упругую
природу (электромагнитная), а
– гравитационную. Когда
– к телу. Эти силы имеют различную
физическую природу: вес – упругую
природу (электромагнитная), а
– гравитационную. Когда
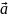 тела относительно Земли отличается от
тела относительно Земли отличается от
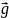 по 2 закону Ньютона :
по 2 закону Ньютона :
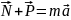 .
Тогда по определению вес тела
.
Тогда по определению вес тела
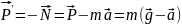 .
При свободном падении тела вместе с
опорой (подвесом) вес
.
При свободном падении тела вместе с
опорой (подвесом) вес
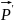 равен нулю, т.к.
равен нулю, т.к.
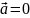 .
Невесомость
– состояние
тела, при кот оно движется только под
действием силы тяжести. Введение сил
инерции позволяет для ИСО ввести
уравнение, подобное 2-ому з Ньютона,
внешний вид которого сохраняется за
счет введения сил инерции.
,
.
Невесомость
– состояние
тела, при кот оно движется только под
действием силы тяжести. Введение сил
инерции позволяет для ИСО ввести
уравнение, подобное 2-ому з Ньютона,
внешний вид которого сохраняется за
счет введения сил инерции.
,
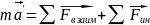 (уравнение
движения в НИСО),
(уравнение
движения в НИСО),
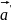 - ускорение в НИСО.
- ускорение в НИСО.
В
механике НИСО: 1). Ускорение тел вызывается
силами, но эти силы не обязательно
обусловлены действием тел друг друга.
2). в НИСО действуют:
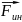 ,
кот присутствуют из-за ускоренного
движения сист
,
кот присутствуют из-за ускоренного
движения сист
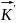 относительно K.
3). Все силы инерции, подробно силам
тяготения, пропорциональны массе тел.
относительно K.
3). Все силы инерции, подробно силам
тяготения, пропорциональны массе тел.
Абсолютное
движение –
движение относительно сист К. Относительное
движение – движение
тела относительно движущейся СО.
Переносное
движение – движение,
кот покоится в системе
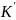 ,
кот движ относительно K.
,
кот движ относительно K.
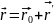 ,
,
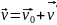 - закон преобразования скорости при
переходе от сит К к сист
- закон преобразования скорости при
переходе от сит К к сист
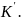
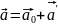 ,
,
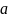 – ускорение в сист К,
– ускорение в сист К,
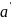 - ускорение в НИСО,
- ускорение в НИСО,
 – переносное ускорение, ускорение
относительно К. Формулы
справедливы только для поступательного
переносного движения.
– переносное ускорение, ускорение
относительно К. Формулы
справедливы только для поступательного
переносного движения.
Силы инерции.
Сила
инерции – векторная
величина, численно равная произведению
мат точки на ее ускорение (ускорение
НИСО) и направленная противоположно
ускорению.
.
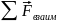 – геометрическая
сумма всех сил, действующих на данное
тело со стороны
других тел,
– геометрическая
сумма всех сил, действующих на данное
тело со стороны
других тел,
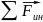 – сумма сил
инерции, действующих на тело.
– сумма сил
инерции, действующих на тело.
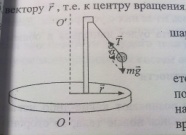
1).
тело покоится во вращающейся с пост
угл скоростью в НИСО:
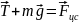 ,
,
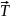 – сила натяжения нити,
– сила натяжения нити,
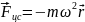 – равнодействующая силы тяжести и силы
натяжения нити.
– равнодействующая силы тяжести и силы
натяжения нити.
 2).
В СО, вращающейся с постоянной
2).
В СО, вращающейся с постоянной
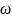 ,
на покоящееся в ней тело действует
центробежная
сила инерции
,
на покоящееся в ней тело действует
центробежная
сила инерции
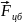 :
:
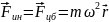 .
Переносное ускорение при этом:
.
Переносное ускорение при этом:
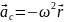 .
.
3).
Тело движется во вращающейся с пост
в НИСО, кот перемещается поступательно
с ускорением
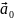 относительно неподвижной ИСО, то
переносное ускорение
относительно неподвижной ИСО, то
переносное ускорение
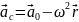 .
Действуют 3 силы: 1. поступательная сила
инерции
.
Действуют 3 силы: 1. поступательная сила
инерции
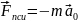 .
Возникает при поступательном движении
НИСО. 2. Центробежная сила инерции
.
Возникает при поступательном движении
НИСО. 2. Центробежная сила инерции
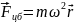 .Действует
во вращающихся СО и на движущиеся, и на
неподвижные тела, удаленные от оси
вращения на конечное расстояние r.
3. кориолисова сила инерции
.Действует
во вращающихся СО и на движущиеся, и на
неподвижные тела, удаленные от оси
вращения на конечное расстояние r.
3. кориолисова сила инерции
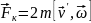 .
Действует во вращающейся системе
координат только на движущиеся с
относительной скоростью
.
Действует во вращающейся системе
координат только на движущиеся с
относительной скоростью
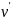 тела. Когда скорость эт движения =0, эта
сила исчезает. Она зависит от угловой
скорости вращения и относительной
скорости вращения. Т.о.
тела. Когда скорость эт движения =0, эта
сила исчезает. Она зависит от угловой
скорости вращения и относительной
скорости вращения. Т.о.
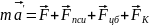 ,
,
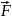 – сумма сил, действующих на тело со
стороны других тел.
– сумма сил, действующих на тело со
стороны других тел.
Си́ла Кориоли́са — одна из сил инерции, существующая в неинерциальной системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения. Названа по имени французского учёного Гюстава Гаспара Кориолиса, впервые её описавшего. Ускорение Кориолиса было получено Кориолисом в 1833 году, Гауссом в 1803 году и Эйлеромв 1765 году.
Причина появления силы Кориолиса — в кориолисовом (поворотном) ускорении. В инерциальных системах отсчёта действует закон инерции, то есть, каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось, требуется придавать телу ускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса.
Для
того, чтобы тело двигалось с кориолисовым
ускорением, необходимо приложение силы
к телу, равной ![]() ,
где
,
где ![]() —
кориолисово ускорение. Соответственно,
тело действует по третьему закону Ньютона с
силой противоположной направленности.
—
кориолисово ускорение. Соответственно,
тело действует по третьему закону Ньютона с
силой противоположной направленности. ![]() Сила,
которая действует со стороны тела, и
будет называться силой Кориолиса. Не
следует путать Кориолисову силу с
другой силой
инерции — центробежной
силой,
которая направлена
по радиусу вращающейся окружности.
Сила,
которая действует со стороны тела, и
будет называться силой Кориолиса. Не
следует путать Кориолисову силу с
другой силой
инерции — центробежной
силой,
которая направлена
по радиусу вращающейся окружности.
Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки — то вправо.
Сила Кориолиса в природе
Сила Кориолиса, вызванная вращением Земли, может быть замечена при наблюдении за движением маятника Фуко[1].
Кроме того, сила Кориолиса проявляется и в глобальных масштабах. В северном полушарии сила Кориолиса направлена вправо от движения, поэтому правые берега рек в Северном полушарии более крутые — их подмывает вода под действием этой силы[2] (см. Закон Бэра). В Южном полушарии всё происходит наоборот. Сила Кориолиса ответственна также и за вращение циклонов и антициклонов[3] (см. геострофический ветер): в Северном полушарии вращение воздушных масс происходит в циклонах против часовой стрелки, а в антициклонах — по стрелке; в Южном — наоборот: по часовой стрелке в циклонах и против — в антициклонах. Отклонение ветров (пассатов) при циркуляции атмосферы — также проявление силы Кориолиса.
Если бы рельсы были бы идеальными, то при движении железнодорожных составов с севера на юг и с юга на север, под воздействием силы Кориолиса один рельс изнашивался бы сильнее, чем второй. В северном полушарии больше изнашивается правый, а в южном левый[4].
Силу Кориолиса необходимо учитывать при рассмотрении планетарных движений воды в океане. Она является причиной возникновения гироскопических волн[5].
При идеальных условиях сила Кориолиса определяет направление закручивания воды например, при сливе в раковине. Однако идеальные условия трудно достижимы. Поэтому феномен «обратного закручивания воды при стоке» является скорее околонаучной шуткой.
