
- •1. Физические модели в механике. Тело отсчета. Система отсчета. Операции с векторами. Время. Траектория. Путь. Перемещение.
- •2. Скорость и ускорение. Нормальное и касательное ускорение.
- •3. Угловые характеристики: перемещение (поворот), скорость и ускорение. Связь между линейными и угловыми кинематическими характеристиками.
- •5. Преобразования координат г. Галилея. Принцип относительности г. Галилея.
- •6. Сила тяжести и вес тела. Закон Гука. Модули упругости, коэффициент Пуассона.
- •7. Сухое и вязкое трение. Формула Ньютона. Виды сухого трения: покоя, скольжения, качения.
- •8. Закон Всемирного тяготения. Напряженность, работа, потенциал гравитационного поля.
- •9. Космические скорости.
- •10. Неинерциальные системы отсчета. Сила инерции. Сила Кориолиса и ее проявление в природе и технике.
- •11. Импульс. Вывод закона сохранения импульса из второго закона динамики. Центр масс системы материальных точек.
- •12. Физические основы космических полетов: законы движения тел переменной массы.
- •13. Энергия как количественная мера движения материи. Работа силы. Мощность. Кинетическая энергия и ее связь с работой.
- •14. Потенциальная энергия. Потенциальное поле. Консервативные силы. Работа в поле потенциальных сил.
- •Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.
- •16. Момент инерции и момент импульса. Уравнение моментов. Основное уравнение динамики вращательного движения.
- •17. Момент инерции твердого тела относительно неподвижной оси вращения. Теорема Штейнера. Моменты инерции тел вращения.
- •18. Кинетическая энергия твердого тела.
- •19. Постулаты Эйнштейна. Преобразования Лоренца. Инварианты преобразований.
- •20. Элементы релятивистской динамики: масса, импульс и энергия. Релятивистская динамика Энергия и импульс
- •[Править]Уравнения движения
- •21. Общие свойства жидкостей и газов. Давление. Закон Паскаля, закон Архимеда. Равновесие, погруженных в жидкость, тел. Идеальная жидкость.
- •Характерные свойства газов, жидкостей и твердых тел.
- •22. Уравнение неразрывности струи. Уравнение Бернулли. Течение вязкой жидкости. Уравнение неразрывности.
- •Уравнение Бернулли.
- •23. Ламинарное и турбулентное течение. Число Рейнольдса. Движение вязкой жидкости в трубе. Формула Пуазейля. Метод Стокса.
- •25. Сложение гармонических колебаний: колебаний одного направления, взаимно перпендикулярных колебаний.
- •§2.1. Сложение гармонических колебаний одного направления.
- •§2.2. Сложение взаимно перпендикулярных колебаний.
- •26. Маятники: физический, математический и пружинный.
- •27. Свободные колебания. Коэффициент затухания, декремент затухания, добротность колебательной системы.
- •28. Вынужденные колебания. Резонанс.
- •29. Понятие волны. Продольные и поперечные волны. Волновое уравнение. Энергия бегущей волны. Вектор Умова. Стоячие волны.
- •Волновое уравнение.
- •Вектор Умова.
- •Стоячие волны.
- •30. Уравнение состояния. Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам.
- •31. Классическая теория теплоемкости идеального газа.
- •33. Политропические процессы. Политропные процессы
- •34. Обратимые и необратимые тепловые процессы. Тепловые двигатели. Обратимые и необратимые тепловые процессы.
- •35. Второе начало термодинамики в формулировке Томсона и Клаузиуса. Цикл Карно. Кпд тепловой машины.
- •36. Энтропия. Закон возрастания энтропии. Цикл Карно в (t,s) – координатах.
- •1. Понятии и общая характеристика энтропии
- •2. Принцип возрастания энтропии
- •37. Термодинамические потенциалы.
- •38. Реальные газы. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса.
- •Отступление от законов идеального газа. Уравнение Ван-дер-Ваальса.
- •3. Изотермы Ван дер Ваальса и их анализ.
- •39. Внутренняя энергия реального газа. Эффект Джоуля-Томсона. Энтальпия.
- •Внутренняя энергия реального газа.
- •Эффект Джоуля—Томсона.
- •40. Свойства жидкостей. Поверхностное натяжение. Явление смачивания.
- •41. Давление под искривленной поверхностью жидкости. Капиллярные явления.
- •42. Свойства твердых тел. Моно- и поликристаллы. Типы кристаллических решеток.
- •43.Дефекты в кристаллах. Теплоемкость твердого тела.
- •44. Фазовые переходы первого рода. Условия равновесия фаз. Диаграмма фазового равновесия. Тройная точка. Фазовые переходы второго рода. Λ-переходы. Фазовые переходы первого рода
- •Примеры фазовых переходов первого рода
- •3.1. Условия равновесия фаз. Фазовые диаграммы
7. Сухое и вязкое трение. Формула Ньютона. Виды сухого трения: покоя, скольжения, качения.
Внешнее трение — механическое сопротивление, возникающее в плоскости касаний двух соприкасающихся, прижатых друг к другу тел при их относительном перемещении. Сила сопротивления, направленная противоположно относительному перемещению тела, называется силой трения, действующей на это тело. На величину внешнего трения влияют: нагрузка, скорость перемещения тел, шероховатость их поверхностей, температура, наличие смазки. Наибольшее значение сила трения имеет в момент «трогания» тела с места. Различают трение покоя, трение скольжения, трение качения и вязкое трение. Сила трения качения обычно значительно меньше силы трения скольжения, а скольжения меньше силы трения покоя.
Сила трения покоя — сила, возникающая между телами при отсутствии относительного движения тел.
Сила трения скольжения — сила, возникающая при движении тел друг по другу.
Сила трения качения — сила, возникающая при вращательном движении одного тела по другому.
Вязкая сила трения — сила, возникающая в газах и жидкостях (сила сопротивления).
Импульс (от лат. impulsus — удар, толчок) — мера механического движения. В механики различают два импульса: импульс силы и импульс массы.
Закон сохранения импульса — закон механики, в соответствии с которым: векторная сумма импульсов тел в замкнутой системе остается постоянной при любых взаимодействиях этих тел между собой и может только перераспределяться между частями системы.
Второй
закон Ньютона в импульсной форме:
из второго закона Ньютона: ![]() получаем
получаем ![]()
8. Закон Всемирного тяготения. Напряженность, работа, потенциал гравитационного поля.
В
рамках классической
механики гравитационное
взаимодействие описывается законом
всемирного тяготения.
Этот закон был открыт Ньютоном в
1666 г.. Он гласит, что сила гравитационного
притяжения между двумя материальными
точками массы ![]() и
и ![]() ,
разделёнными расстоянием
,
разделёнными расстоянием ![]() ,
пропорциональна обеим массам и обратно
пропорциональна квадрату расстояния
между ними — то есть:
,
пропорциональна обеим массам и обратно
пропорциональна квадрату расстояния
между ними — то есть:
![]()
Здесь ![]() — гравитационная
постоянная, равная
— гравитационная
постоянная, равная ![]() м³/(кг
с²).
м³/(кг
с²).
Напряженность
 гравитационного поля – векторная
характеристика поля:
гравитационного поля – векторная
характеристика поля:
 .
– сила, действующая на тело массы 1 кг.
Силы тяготения имеют потенциальный
характер, что позволяет ввести скалярную
характеристику гравитационного поля
– потенциал
.
– сила, действующая на тело массы 1 кг.
Силы тяготения имеют потенциальный
характер, что позволяет ввести скалярную
характеристику гравитационного поля
– потенциал
 ,
связанный с
соотношением:
,
связанный с
соотношением:
 .
Для грав поля, создаваемого мат точкой
с массой М, находящейся в начале координат,
напряженность равна:
.
Для грав поля, создаваемого мат точкой
с массой М, находящейся в начале координат,
напряженность равна:
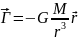 ,
– радиус-вектор точки поля, в кот
определяется
.
Работа сил
гравитационного поля,
например Земли, не зависит от формы
пути, а от начального и конечного
положения тела. При перемещении тела с
расстояния
,
– радиус-вектор точки поля, в кот
определяется
.
Работа сил
гравитационного поля,
например Земли, не зависит от формы
пути, а от начального и конечного
положения тела. При перемещении тела с
расстояния
 :
:
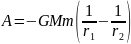 .
Потенциал
гравитационного поля
зависит от массы тела, создающего грав
поле, и расстоянием от центра данного
тела до нек точки поля:
.
Потенциал
гравитационного поля
зависит от массы тела, создающего грав
поле, и расстоянием от центра данного
тела до нек точки поля:
 .
Потенциальная эн тела вблизи пов Земли:
.
Потенциальная эн тела вблизи пов Земли:
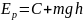 ,
где постоянная С на пов Земли принимается
равной 0. Тогда
вблизи пов Земли определяется как:
,
где постоянная С на пов Земли принимается
равной 0. Тогда
вблизи пов Земли определяется как:
 .
.
9. Космические скорости.
Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении с поверхности небесного тела сможет:
v1 (круговая скорость) — стать спутником небесного тела (то есть вращаться по круговой орбите вокруг НТ на нулевой или пренебрежимо малой высоте относительно поверхности);
v2 (параболическая скорость, скорость убегания) — преодолеть гравитационное притяжение небесного тела и уйти на бесконечность;
v3 — покинуть звёздную систему, преодолев притяжение звезды;
v4 — покинуть галактику.
Космические скорости.
Первая космическая скорость — скорость, которую необходимо придать баллистическому снаряду, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы поместить его на круговую орбиту с радиусом равном радиусу планеты. Иными словами, первая космическая скорость — это скорость, с которой надо бросить камень в горизонтальном направлении, чтобы он больше не упал на Землю. Для вычисления первой космической скорости необходимо рассмотреть равенство центробежной силы и силы тяготения действующих на снаряд на круговой орбите.

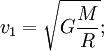
где m — масса снаряда, M — масса планеты, G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2),
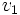 —
первая космическая скорость, R —
радиус планеты. Подставляя численные
значения (для Земли, M = 5,97·1024 кг,
R = 6 378 000 м), найдем
—
первая космическая скорость, R —
радиус планеты. Подставляя численные
значения (для Земли, M = 5,97·1024 кг,
R = 6 378 000 м), найдем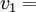 7,9 км/с
7,9 км/с
Первую космическую скорость можно определить через ускорение свободного падения — так как g = GM/R², то
 .
.
Первой космической скорости недоста точно для того, чтобы тело могло выйти из сферы земного притяжения. Необходимая для этого скорость называется второй кос мической. Второй космической (или пара болической) скоростью v2 называют ту наименьшую скорость, которую надо со общить телу, чтобы оно могло преодолеть притяжение Земли и превратиться в спут ник Солнца, т. е. чтобы его орбита в поле тяготения Земли стала параболической. Для того чтобы тело (при отсутствии со противления среды) могло преодолеть земное притяжение и уйти в космическое пространство, необходимо, чтобы его кине тическая энергия была равна работе, совершаемой против сил тяготения:
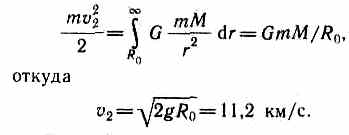
Между первой и второй космическими скоростями существует простое соотношение:

Для того чтобы покинуть пределы солнечной системы, тело должно преодолеть, кроме сил притяжения к земле, также и силы притяжения к Солнцу. Необходимая для этого скорость запуска тела с поверхности Земли называется третьей космической скоростью V3. Скорость V3 зависит от направления запуска. При запуске в направлении орбитального движения Земли эта скорость минимальна и составляет около 17 км/с. При запуске в направлении, противоположном направлению движения Земли, V3 равняется примерно 73 км/с.
