2. Скорость и ускорение. Нормальное и касательное ускорение.

Скорость и ускорение. Вычисление пройденного пути.

Скорость – векторная физическая величина, которая определяет как быстроту движения, так и его направление в данный мом вр. Вектор средней скорости за интервал времени – отношение приращения радиус-вектора точки к промеж вр: 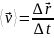. Мгновенная скорость мат точки – средняя скорость за бесконечно малый инт вр, определяемая как векторная величина, равная первой производной по вр от радиус-вектора рассматриваемой точки: 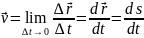. Вектор мгновенной скорости напрвлен по касательной к траектории в сторону движения. В неравномерном движении модуль мгновенной скорости с течением времени изменяется средняя скорость неравномерного движения (средняя путевая скорость) – пройденное телом расстояние s, деленное на время, затраченное на прохождение этого расстояния: 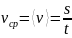. -> 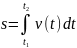. Равномерное движение – точка за любые равные промеж вр проходит равные расстояния. Ускорение – векторная величина, определяемая как изменение скорости в ед вр: 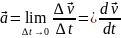. Кинематический закон изменения скорости: .

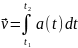Тангенциальное и нормальное ускорения. Угол между векторами скорости и ускорения.

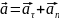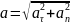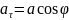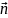, , где , . Единичный вектор касательной направлен по касательной к траектории сторону движения точки, единичный вектор главной нормали направлен к центру кривизны. Орты и всегда перпендикулярны друг другу. Тангенциальное и нормальное ускорения характеризуют соответственно изменение скорости по величине и изменение направления вектора скорости точки: , . Равнопеременное движение –

. Любое криволинейное движение можно разбить на участки каждой из кот будет эл окружности.

3. Угловые характеристики: перемещение (поворот), скорость и ускорение. Связь между линейными и угловыми кинематическими характеристиками.

Частным случаем криволинейного движения – является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением.

где r – радиус окружности.

Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.

Кроме центростремительного ускорения, важнейшими характеристиками равномерного движения по окружности являются период и частота обращения.

Вращательное движение тела или точки характеризуется углом поворота, угловой скоростью и угловым ускорением.

Угол поворота φ - это угол между двумя последовательными положениями радиуса вектора r, соединяющего тело или материальную точку с осью вращения. Угловое перемещение измеряется в радианах.

Угловая скорость (w) – векторная физическая величина, показывающая, как изменяется угол поворота в единицу времени и численно равная первой производной от угла поворота по времени, т.е

.

Направление вектора угловой скорости совпадает с направлением вектора углового перемещения, т.е. вектора, численно равного углу φ и параллельного оси вращения; оно определяется по правилу буравчика: если совместить ось буравчика с осью вращения и поворачивать его в сторону движения вращающейся точки, то направление поступательного перемещения буравчика определит направление вектора угловой скорости. Точка приложения вектора произвольна, это может быть любая точка плоскости, в которой лежит траектория движения. Удобно совмещать этот вектор с осью вращения.

При равномерном вращении численное значение угловой скорости не меняется, т.е. ω = const. Равномерное вращение характеризуется:

- периодом вращения Т, т.е. временем, за которое тело делает один полный оборот, период обращения измеряется в с;

- частотой, измеряемой в Гц и показывающей число оборотов в с;

- круговой (циклической,угловой) частотой (это та же самая угловая скорость).

Угловая скорость может меняться как по величине, так и по направлению. Векторная величина, характеризующая изменение угловой скорости в единицу времени и численно равная второй производной от углового перемещения по времени, называется угловым ускорением:

Если положение и радиус окружности, по которой происходит вращение не изменяется со временем, то направление векторов углового ускорения и угловой скорости совпадают, если вращение ускоренное, и противоположны, если вращение замедленное.

При равномерном движении по окружности тангенциальная составляющая ускорения равна нулю, т.е. модуль линейной скорости постоянен и определяется соотношением Но т.к. направление скорости постоянно изменяется, то существует нормальное ускорение Т.о., линейная скорость направлена по касательной к окружности в каждой точке по движению; ускорение перпендикулярно скорости и направлено к центру кривизны.

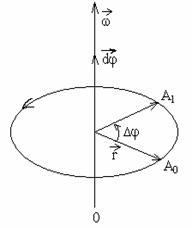
Связь между линейными и угловыми величинами, характеризующими движение

Отдельные точки вращающегося тела имеют различные линейные скорости v, которые непрерывно изменяют свое направление и зависят от угловой скорости ω и расстояния r соответствующей точки до оси вращения. Точка, находящаяся на расстоянии r от оси вращения проходит путь ΔS = rΔφ. Поделим обе части равенства на

Переходя к пределам при , получим или .

Таким образом, чем дальше отстоит точка от оси вращения, тем больше ее линейная скорость. По определению ускорения, или

что значения линейной скорости, тангенциального и нормального ускорений растут по мере удаления от оси вращения. Формула устанавливает связь между модулями векторов v, r, ω, которые перпендикулярны друг к другу.

4. Сила как физическая величина. Свойства сил. Инерция. I закон динамики (закон инерции). Инерциальная система отсчета. Опыты Г. Галилея. Масса. Импульс. II закон динамики в формулировке Ньютона и его современная трактовка. III закон динамики.

I ЗАКОН НЬЮТОНА (закон инерции) – существуют такие СО, в кот. свободная (уединенная) частица движется не ускоренно, т.е. равномерно и прямолинейно, если равнодействующая внешних сил, приложенных к частице =0 (или силы не действуют). Такие СО наз инерциальными, а движение – по инерции. Инертность – свойство тела сохранять состояние покоя или равномерного прямолинейного движения. Любая другая СО, движущаяся равномерно и прямолинейно относительно ИСО, явл также инерциальной. Пример ИСО: гелиоцентрическая СО с центром на Солнце и осями, проведенными в направлении определенных звезд. В ИСО сила F – векторная величина, являющаяся мерой механического воздействия на тело со стороны др тел или полей, в рез кот тело получает ускорение или изменяет форму и размеры. Каждый вид сил задается силовым законом. Физическое поле задано, если каждой точке пространства задается определенное значение нек физ величины. Прямая, вдоль кот направлена сила, наз линией действия силы. Механическая система – совокупность мат точек (тел), рассматриваемых как единое целое. Внешние тела – не входят в состав исследуемой системы. Внешние силы – действуют на систему со стороны внешних тел. Внутренние силы – силы взаимодействия между частями рассматриваемой системы. Стационарное поле – неизменяющееся с течением времени поле, действующее на на мат точку. Масса – физ величина, являющаяся мерой инертности мат точки или мерой инертности тела при поступательном движении. В рамках ньютоновской механики масса тела служит мерой содержащегося в теле вещества и выполняются законы сохранения и аддитивности: масса изолированной системы тел не изменяется со временем и равна сумме масс тел, составляющих систему. Плотность – отношение массы малого эл тела к величине объема этого элемента: 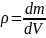. Импульс (количество движения) – совпадает по направлению со скоростью; величина аддитивная. Импульс системы, состоящей из n мат точек, равен вект сумме импульсов всех точек системы.

Второй закон Ньютона как уравнение движения.

В ИСО справедлив второй закон Ньютона: ускорение, получаемое мат точкой , пропорционально его силе, совпадает с ней по направлению и обратно пропорционально массе мат точки (тела):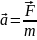 . Более общая формулировка второго закона Ньютона – основной закон динамики мат точки: скорость изменения импульса мат точки равна действующей силе (и по модулю, и по направлению): . 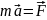– уравнение движения мат точки. Одновременное действие на мат точку нескольких сил 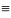действию одной силы, называемой равнодействующей силой и равной их геометрической сумме:

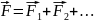
Третий закон Ньютона. Законы сил.

Общее свойство всех сил взаимодействия постулировано в 3-ем законе Ньютона: силы взаимодействия 2-ух мат точек в ИСО всегда равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки: 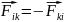. Принцип дальнодействия: взаимодействие между телами распространяется в пространстве с б.б.скоростью. При скоростях << скорости света 2 и 3 законы Ньютона выполняются с большой точностью. подтверждает ЗСИ в ИСО. Парность взаимодействия: сила, с кот взаимодействуют 2 тела (мат точки), зависит только от их относительного положения и относительной скорости движения.