Вопрос 12. Обратная матрица. Вычисление обратной матрицы.
Обратную
матрицу 
можно
найти по следующей формуле:
,
где 
–
определитель матрицы 
, 
–
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы
.
Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Обозначения: Как
Вы уже, наверное, заметили, обратная
матрица обозначается надстрочным
индексом 
Начнем с простейшего случая – матрицы «два на два». Чаще всего, конечно, требуется найти обратную матрицу для матрицы «три на три», но, тем не менее, настоятельно рекомендую изучить более простое задание, для того чтобы усвоить общий принцип решения.
Пример:
Найти
обратную матрицу для матрицы 
Решаем. Последовательность действий удобно разложить по пунктам.
1)
Сначала находим определитель матрицы.
Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
В
рассматриваемом примере, как выяснилось, 
,
а значит, всё в порядке.
2)
Находим матрицу миноров 
Для решения нашей задачи не обязательно знать, что такое минор, однако, желательно ознакомиться со статьей Как вычислить определитель.
Матрица
миноров имеет такие же размеры, как и
матрица
,
то есть в данном случае 
.
Дело
за малым, осталось найти четыре числа
и поставить их вместо звездочек.
Возвращаемся
к нашей матрице
Сначала
рассмотрим левый верхний элемент
Как
найти его минор?
А
делается это так: МЫСЛЕННО вычеркиваем
строку и столбец, в котором находится
данный элемент:
Оставшееся
число и является минором
данного элемента,
которое записываем в нашу матрицу
миноров:
Рассматриваем
следующий элемент матрицы
:
Мысленно
вычеркиваем строку и столбец, в котором
стоит данный элемент:
То,
что осталось, и есть минор данного
элемента, который записываем в нашу
матрицу:
Аналогично
рассматриваем элементы второй строки
и находим их миноры:
Готово.
–
матрица миноров
соответствующих элементов матрицы
.
3)
Находим матрицу алгебраических
дополнений 
Это
просто. В матрице миноров нужно ПОМЕНЯТЬ
ЗНАКИ у
двух чисел:
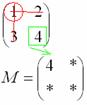
Именно
у этих чисел, которые я обвел в кружок!
–
матрица алгебраических
дополнений соответствующих элементов
матрицы
.
И всего-то лишь…
4) Находим транспонированную матрицу алгебраических дополнений .
Что такое транспонирование матрицы, и с чем это едят, смотрите в лекции Действия с матрицами.
–
транспонированная
матрица алгебраических дополнений
соответствующих элементов матрицы
.
5) Ответ.
Вспоминаем нашу формулу Всё найдено!
Таким
образом, обратная матрица:
Вопрос 13. . Ранг матрицы. Практические приёмы вычисления ранга матрицы.
Определение
4.1. Минором
порядка 
матрицы 
называется
определитель квадратной матрицы,
образованной из элементов исходной
матрицы, находящихся на пересечении
каких-либо выбранных
строк
и
столбцов
матрицы 
Определение
4.2.
В матрице
порядка 
минор
порядка 
называется
базисным, если он не равен нулю, а все
миноры порядка 
и
выше равны нулю, или не существуют вовсе.
Определение
4.3. Порядок
базисного минора матрицы
называется
рангом матрицы
и обозначается символом 
Замечание. Из приведённых определений следует, что ранг матрицы равен наибольшему из порядков её миноров, отличных от нуля.
Одним из способов вычисления ранга матрицы является метод окаймления миноров. Рассмотрим применение этого способа на следующем примере.
Пример. Определить
ранг матрицы 
Среди
миноров второго порядка матрицы
существует,
по крайней мере, один, отличный от нуля.
Например, минор матрицы 
полученный
вычёркиванием из этой матрицы третьей
строки, третьего, четвёртого и пятого
столбцов, отличен от нуля:
следовательно, ранг данной матрицы не меньше двух.
Найдём
миноры третьего порядка матрицы 
Все
десять миноров третьего порядка равны
нулю, поэтому ранг данной матрицы не
может быть равен трём. Таким образом, 
Другой способ вычисления ранга матрицы основан на применении элементарных преобразований матрицы и использовании следующих утверждений.
Теорема 4.1. Ранг ступенчатой матрицы равен количеству её ненулевых строк.
Теорема 4.2. Элементарные преобразования матрицы не изменяют её ранг.
Пример. Вычислим
ранг матрицы из предыдущего примера.
Для этого матрицу
с
помощью элементарных преобразований
приведём к ступенчатому виду. Найдём
сумму второй строки матрицы
с
первой строкой, умноженной на 
а
также сумму третьей строки матрицы
с
первой строкой, умноженной на 
В результате
указанных элементарных преобразований
получим эквивалентную матрицу
Третью
строку полученной матрицы сложим с её
первой строкой, умноженной на
и
получимэквивалентную матрицу
Удалим
из этой матрицы третью строку и получим
ступенчатую эквивалентную матрицу,
количество ненулевых строк которой
равно двум:
В соответствии с теоремой 4.1, ранг полученной матрицы равен двум, а значит (теорема 4.2),