§2. Линейно зависимые и линейно независимые системы элементов.

Определение 1. Сумма   называется линейной комбинацией элементов а₁, а₂,…,а_n  с коэффициентами λ_k .

Определение 2. Система элементов линейного пространства {a₁,…,a_n} называется линейно зависимой, если найдутся коэффициенты  λ₁,…,λ_n  не все равные нулю, линейная комбинация с которыми равна нулю, т.е.                                                 

Определение 3. Система элементов линейного пространства {a₁,…,a_n} называется линейно

независимой, если ее линейная комбинация равна нулю только с нулевыми коэффициентами: 

Имеют место несколько простых утверждений.

Теорема 1 (необходимое и достаточное условие линейной независимости).  a₁,…,a_n – линейно зависима   когда хотя бы один из элементов является линейной комбинацией остальных.

Теорема 2. Если один из элементов системы равен нулю, то вся система линейно зависима.

{ }

Теорема 3. Если подсистема линейно зависима, то и вся система линейно зависима.

{ }

 Евклидовы пространства.

Определение 1. Линейное пространство E = {f, g, h, …} называется евклидовым, если 

ставится  в соответствие число, называемое скалярным произведением: . При этом, для      выполняются аксиомы:

 

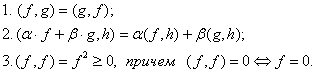
§8. Линейные операторы.

Определение 1. Функция (отображение) А, определенная на линейном пространстве L_n , область значений которой принадлежит линейному пространству  L_m (здесь n и m – размерности соответствующих пространств) называется оператором : 

 Если   

 Все прообразы нулевого элемента L_m называют ядром оператора  А: 

Определение 2. Оператор  А  называется линейным, если для   выполняется равенство: 

Определение 3. Матрицей линейного оператора  А  называется матрица (будем обозначать ее  через А_mn ), столбцами которой являются координаты образов базисных элементов {e} в базисе  {f}, т.е. , если

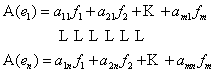     , то 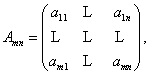  или в матричной форме:

  

Замечание. Оператор, в частности линейный, определяет некоторое действие на элементы линейного пространства и не зависит от базиса. В свою очередь, матрица линейного операторазависит как от базиса пространства прообразов, так и от базиса пространства  образов.

Теорема 1. Образ вектора  х  равен произведению матрицы линейного оператора на столбец его            координат: если  у = А(х),  то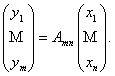          

 

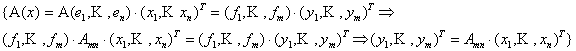
Таким образом, каждому линейному оператору ставится в соответствие матрица. Верно и обратное: каждой матрице можно поставить в соответствие линейный оператор. {Зададим оператор  А формулой 

 } 

В настоящем курсе используются операторы, прообразы и образы которых принадлежат  одному и тому же линейному пространству  L . Матрицы таких операторов квадратные, а образы и прообразы, естественно, представляются в едином базисе. Будем обозначать матрицу оператора  А  как  A_n (n – размерность пространства), либо  A_e ( {e} - базис пространства).  В дальнейшем будем рассматривать только такие операторы.

Одной из особенностей этих операторов является наличие определителя у его матрицы.

Определение 4. Линейный оператор из  L в L , определитель матрицы которого равен нулю, называется вырожденным и невырожденным в противном случае.

Замечание. Матрицу невырожденного оператора можно рассматривать как матрицу перехода от одного базиса к другому.

Теорема 2. При переходе к новому базису матрица линейного оператора меняется по        следующему закону:   

{Пусть {f} – новый базис, {e} – старый. 1)   (§5,8);

 2)   }

Следствие. Определитель матрицы линейного оператора не зависит от базиса.

{ }

Определение 4. Матрицы  А   и      называются подобными.

Свойства подобных матриц:

1.   { см. выше}

2.  матрица обратная к подобной подобна обратной матрице.