§9. Действия с линейными операторами.

Рассмотрим множество линейных операторов  Определим на этом множестве операции сложения, умножения на число и произведение операторов:  А + В, λА  и  А·В.

1. 

2. 

3. 

Легко проверить, что все указанные операторы – линейные.  {проверим для  А·В :

(АВ)(αх +βу) = А(αВ(х) + βВ(у)) = α(АВ)(х) +β(АВ)(у) }

Этим операторам соответствуют матрицы: 

{ для двух первых действий – очевидно; (3):   }

                                              Свойства линейных операций: 

              1. А  + В = В +А ;                                             5. λ( μА ) = (λμ)А ;

              2. ( А + В ) + С = А + ( В + С ) ;                    6. 1·А = А ;

              3. А + Ø = А ;                                                  7. (λ + μ)А = λА + μА ;

              4. А + (−А ) = Ø ;                                            8. λ( А + В ) = λА + λВ ;

Из этих соотношений следует, что множество линейных операторов образует линейное пространство (размерности  n² ).

                                        Свойства произведения операторов:

            1. (λА)·В = λ ( А·В) ;                                           3.( А + В )·С = А·С + В·С ;                           

            2. А·( В·С ) = ( А·В )·С ;                                     4. А·( В + С ) = А·В + А·С ;

Произведение операторов позволяет ввести понятие степени оператора:

А¹ = А, А² = А·А  и т.д.   (тождественному оператору:  , его матрица, очевидно, равна единичной). Так же, по определению, вводится понятие обратного

оператора:   Он обладает следующим свойством: если у = А(х),

то    Ясно, что его матрица равна обратной матрице исходного  ( ) и он существует только у невырожденных операторов.

Пример. 

 

Вопрос 6. Сложение векторов, умножение векторов на числа. Вычитание векторов.

Суммой двух векторов и называется вектор , направленный из начала вектора в конец вектора при условии, что начало совпадет с концом вектора . Если векторы заданы их разложениями по базисным ортам, то при сложении векторов складываются их соответствующие координаты.

Рассмотрим это на примере декартовой системы координат. Пусть

Покажем, что

Из рисунка 3 видно, что

Сумма любого конечного числа векторов может быть найдена по правилу многоугольника (рис. 4): чтобы построить сумму конечного числа векторов, достаточно совместить начало каждого последующего вектора с концом предыдущего и построить вектор, соединяющий начало первого вектора с концом последнего.

Свойства операции сложения векторов:

В этих выражениях m, n - числа.

Разностью векторов и называют вектор Второе слагаемое является вектором, противоположным вектору по направлению, но равным ему по длине.

Таким образом, операция вычитания векторов заменяется на операцию сложения

Вектор , начало которого находится в начале координат, а конец - в точке А (x1, y1, z1), называют радиус-вектором точки А и обозначают или просто . Так как его координаты совпадают с координатами точки А, то его разложение по ортам имеет вид

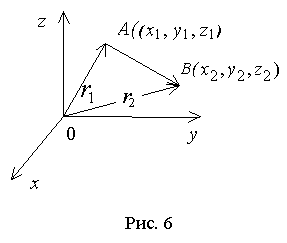
Вектор , имеющий начало в точке А(x1, y1, z1) и конец в точке B(x2, y2, z2), может быть записан в виде

где r₂- радиус-вектор точки В; r₁- радиус-вектор точки А.

Поэтому разложение вектора по ортам имеет вид

Его длина равна расстоянию между точками А и В

УМНОЖЕНИЕ

Так в случае плоской задачи произведение вектор на a = {ax; ay} на число b находится по формуле

a · b = {ax · b; ay · b}

Пример 1. Найти произведение вектора a = {1; 2} на 3.

Решение

3 · a = {3 · 1; 3 · 2} = {3; 6}

Так в случае пространственной задачи произведение вектора a = {ax; ay; az} на число b находится по формуле

a · b = {ax · b; ay · b; az · b}

Пример 1. Найти произведение вектора a = {1; 2; -5} на 2.

Решение

2 · a = {2 · 1; 2 · 2; 2 · (-5)} = {2; 4; -10}

Скалярное произведение векторов и где - угол между векторами и ; если либо , то

Из определения скалярного произведения следует, что

где, например, есть величина проекции вектора на направление вектора .

Скалярный квадрат вектора:

Свойства скалярного произведения:

Скалярное произведение в координатах

Если то

Угол между векторами

Угол между векторами — угол между направлениями этих векторов (наименьший угол).

Векторное произведение(Векторное произведение двух векторов. )— это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность строить вектор, перпендикулярный двум имеющимся — векторное произведение предоставляет эту возможность. Векторное произведение полезно для «измерения» перпендикулярности векторов — длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.

Векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.

В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности»

Коллинеарность векторов.

Два ненулевых (не равных 0) вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой. Допусти́м, но не рекомендуется синоним — «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).

Сме́шанное произведе́ние векторов(a, b,c) — скалярное произведение вектора a на векторное произведение векторов b и c:

(a,b,c)=a ⋅(b ×c)

иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).

Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами( a,b,c) .

Свойства

Смешанное произведение кососимметрично по отношению ко всем своим аргументам:т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что Смешанное произведение в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов и :

Смешанное произведение в левой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов и , взятому со знаком "минус":

В частности,

Если любые два вектора параллельны, то с любым третьим вектором они образуют смешанное произведение равное нулю.

Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.

Геометрический смысл — Смешанное произведение по абсолютному значению равно объёму параллелепипеда (см. рисунок), образованного векторами и ; знак зависит от того, является ли эта тройка векторов правой или левой.

Компланарность векторов.

Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости

Свойства компланарности

Если хотя бы один из трёх векторов — нулевой, то три вектора тоже считаются компланарными.

Тройка векторов, содержащая пару коллинеарных векторов, компланарна.

Смешанное произведение компланарных векторов . Это — критерий компланарности трёх векторов.

Компланарные векторы — линейно зависимы. Это — тоже критерий компланарности.

В 3-мерном пространстве 3 некомпланарных вектора образуют базис.