60.Биномиальный интеграл.

Биномиальным дифференциалом наз-ся выражение , где , и - рациональные числа.

Интеграл от биномиального дифференциала приводится к интегралу от рациональной функции в следующих трех случаях.

Случай 1. Показатель степени - целое число. Тогда интеграл сводится к интегралу от рациональной функции с помощью подстановки , где - общий знаменатель дробей и .

Случай 2. Число - целое. Тогда сводится к интегралу от рац.функции с помощью подстан. , - знаменатель дроби .

Случай 3. Число - целое. Тогда интеграл рационализируется с помощью подстановки , где - знаменатель дроби .

Пример. Найти интеграл .

Здесь , , - целое число, т.е. имеет место первый случай интегрируемости. Поэтому следует применить подстановку , тогда , и данный интеграл принимает вид

61.Интегрирование функции .

Рассмотрим интегралы вида . Такие интегралы могут быть сведены к интегралам от рациональных функций заменой переменной , где . Действительно , , , .

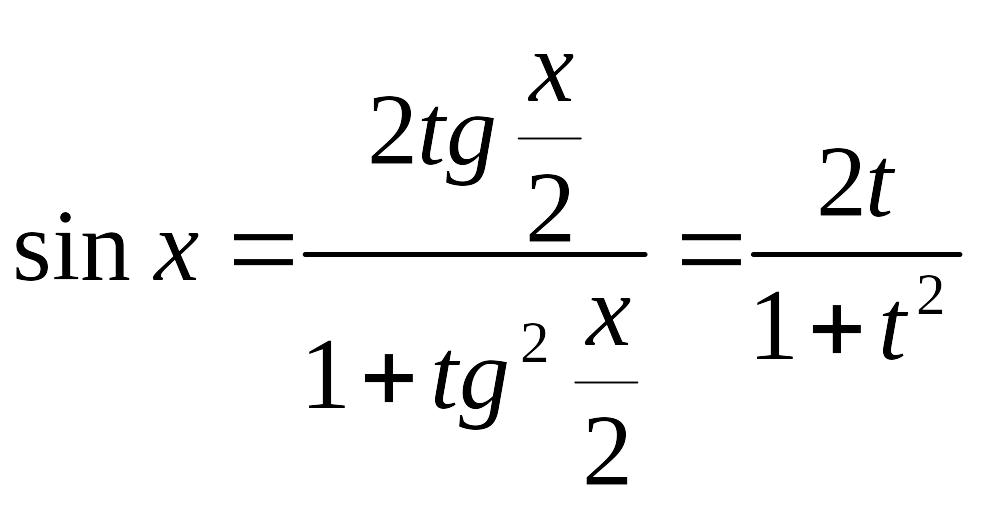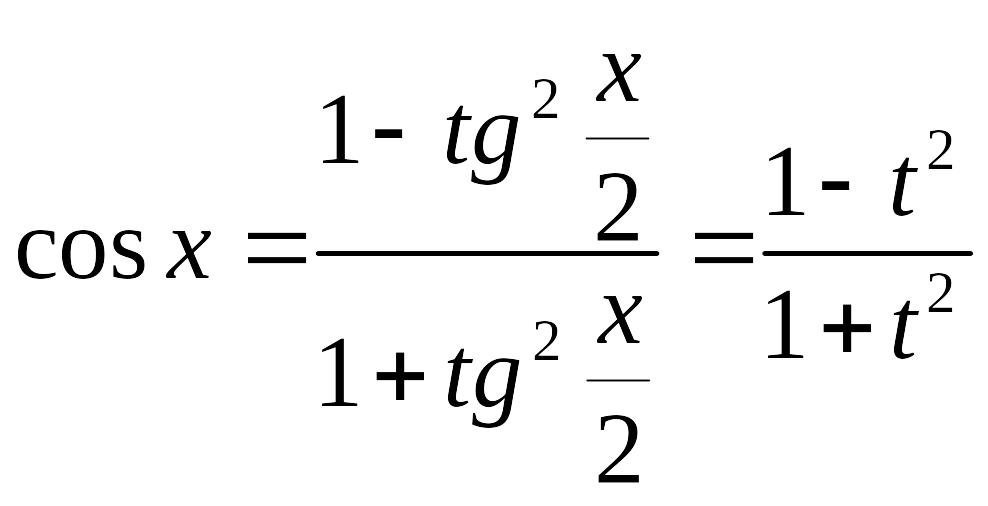Пример. Вычислить .

.

62.Определенный интеграл и его геометрический смысл.

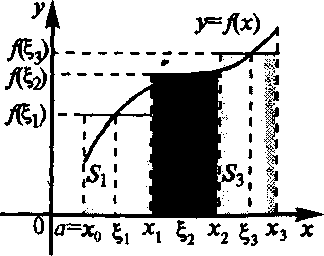Пусть функция неотрицательна на . Отдельное слагаемое интегральной суммы в этом случае равно площади прямоугольника со сторонами и , Другими словами, - это площадь под прямой на отрезке . Поэтому вся интегральная сумма равна площади под ломаной, образованной на каждом из отрезков прямой , параллельной оси абсцисс.

Определение. Пусть предел интегральной суммы при стремлении к нулю существует, конечен и не зависит от способа выбора точек , , … и точек , , ... Тогда этот предел называется определенным интегралом от функции на , обозначается , а сама функция называется интегрируемой на отрезке , т.е. .

Геометрический смысл определенного интеграла. Определенный интеграл численно равен площади криволинейной трапеции

63.Основные свойства определенного интеграла.

1. Постоянный множитель можно выносить за знак интеграла, т.е. .

2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е. .

3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. .

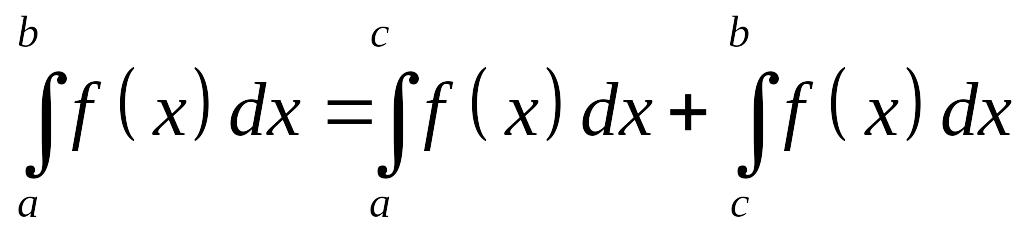64.Замена переменной в определенном интеграле

Теорема. Пусть функция имеет непрерывную производную на отрезке , , и функция непрерывна в каждой точке вида , где . Тогда справедливо следующее равенство .

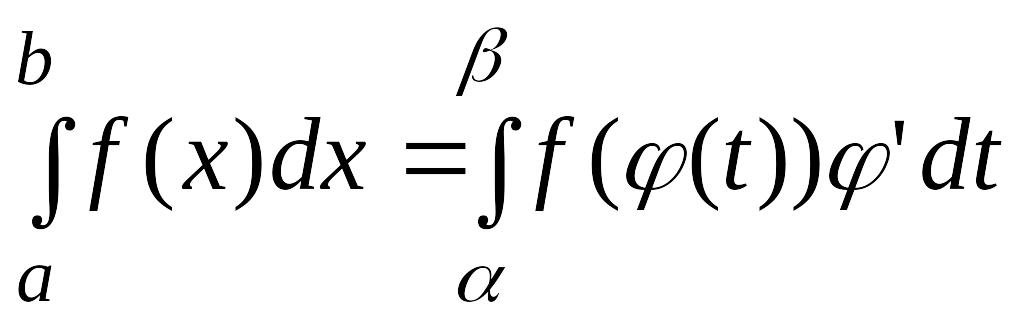Пример. Вычислить определенный интеграл .

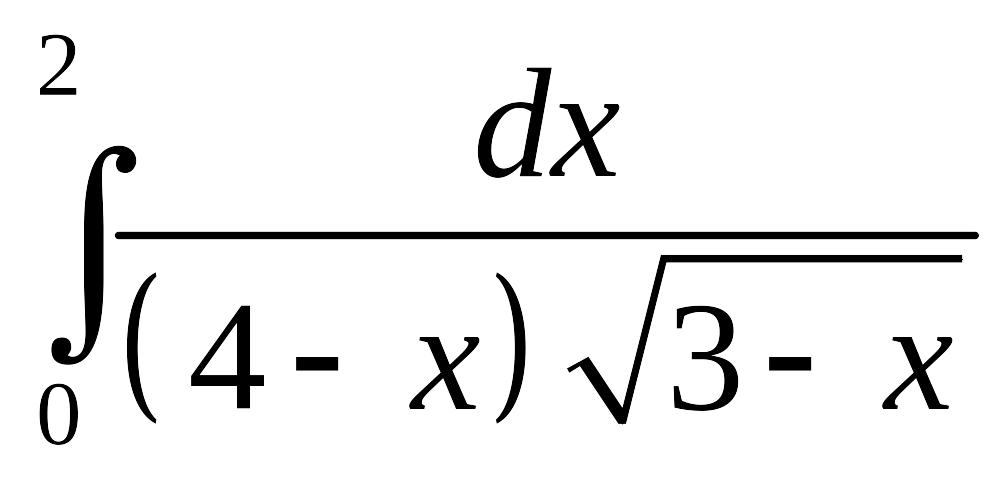Пусть , , , , , тогда .

65.Вычисление определенного интеграла по частям.

Теорема. Пусть функции и имеют непрерывные производные на отрезке . Тогда .

Пример. Вычислить .

Пусть , , , , тогда .Вычислим . .

Итак, .

Вопрос 67. Интеграл с переменным верхним пределом. Интегралы по бесконечным промежуткам.

Интеграл с переменным верхним пределом

Рассмотрим функцию   , заданную на отрезке   , и предположим, что она интегрируема на отрезке   . Тогда при любом   эта функция будет интегрируема на отрезке   и, следовательно, функция

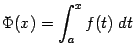
определена при всех   . При   мы по определению положим её равной 0, то есть будем считать, что   для любой функции   и точки   из её области определения. Итак, функция   равняется значению определённого интеграла с переменным верхним пределом, вычисленного от интегрируемой функции   , не обязательно непрерывной.

        Теорема 3.11   Функция   , определённая выше, непрерывна при всех   для любой интегрируемой функции   .

        Доказательство.     Заметим, что если функция   положительна, то значение   интерпретируется как площадь под графиком   , лежащая над отрезком   . Если дать   приращение   , то площадь получит приращение в виде площади полоски, лежащей над отрезком   (см. рис.).

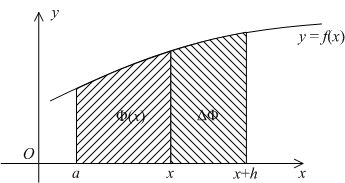
Рис.3.4.

Эта площадь, вследствие ограниченности интегрируемой функции, мала, если приращение   мало; это и означает непрерывность функции   в точке   .

Проведём теперь более аккуратные рассуждения, не предполагая, что функция принимает положительные значения.

Пусть фиксирована точка   и взято такое приращение   , что   . Пользуясь аддитивностью интеграла, получаем, что

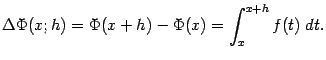
Согласно неравенству (3.5),

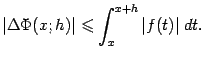
Но по теореме 3.5 функция   ограничена, поэтому существует такая постоянная   , что   при всех   и, в том числе, при   . Воспользовавшись теоремой об интегрировании неравенства, получаем, что

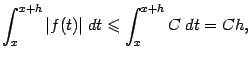
откуда

При   получаем по теореме "о двух милиционерах", что   и   , что означает, что функция   непрерывна справа в любой точке   .

Рассматривая аналогично отрезок   при   и   , получаем, что

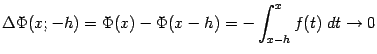
при   , что означает непрерывность функции   слева в любой точке   .

Тем самым функция   непрерывна справа в точке   , непрерывна слева в точке   и непрерывна (с обеих сторон) в любой точке   , что и требовалось доказать.      

        Теорема 3.12   Пусть функция   непрерывна на отрезке   и функция   определена всё той же формулой. Тогда   имеет производную в любой точке интервала   , производную справа в точке   и производную слева в точке   , причём эти производные совпадают со значением функции   в соответствующей точке:

 при   и 

        Доказательство.     Снова рассмотрим приращение   при   ,   ,   . Поскольку функция   непрерывна, мы можем применить теорему о среднем к интегралу по отрезку   :

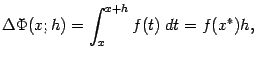
где    -- некоторая точка отрезка   . Получаем, деля на   :

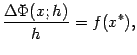
откуда при   из непрерывности   следует, что

поскольку   при   . Получили, что правая производная совпадает с   во всех точках   .

Аналогично доказывается, что левая производная   совпадает с   во всех точках   Во внутренних точках   совпадение производных слева и справа со значением   означает, что функция   имеет производную   , равную   .      

Точно так же доказывается, что производная интеграла

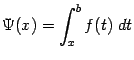
от непрерывной функции   по переменному нижнему пределу равняется   :

Равенство   означает, что функция   является первообразной для   на интервале   . Другая первообразная -- это, очевидно, функция   .

Итак, мы получили важный результат о наличии первообразной у любой непрерывной функции:

        Теорема 3.13   Пусть    -- непрерывная на интервале   функция. Тогда на интервале   функция   имеет некоторую первообразную   , то есть   при всех   .

        Доказательство.     Для доказательства достаточно фиксировать произвольную точку   и положить

При   эти определения не противоречат друг другу, поскольку и та, и другая формулы дают   .

Нетрудно видеть, что при   получается   , при   получаем   . При   производная слева даёт значение   , а производная справа -- значение   , так что производные слева и справа совпадают и   , что и завершает доказательство.      

Пусть теперь    -- произвольная первообразная для непрерывной функции   , заданной на некотором интервале   , содержащем отрезок   . Мы уже проверили, что функция   , такая что   при   служит тогда первообразной для     , а поскольку любые первообразные для одной и той же функции на заданном интервале могут отличаться лишь постоянным слагаемым, получаем, что

где   , при всех   , в том числе и при   и   . Получаем   и   , откуда

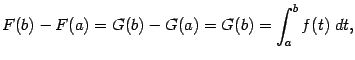
поскольку   Итак, меняя обозначение переменной интегрирования на   , получаем в итоге формулу

(3.6)

где    -- произвольная первообразная для функции   . Эта формула называется формулой Ньютона - Лейбница. Она играет ключевую роль в интегральном исчислении и во всём математическом анализе.

Напомним, что мы получили её в предположении, что функция   непрерывна. Если функция   имеет разрыв на отрезке   , то разность значений первообразной может не иметь никакого отношения к величине определённого интеграла. Поэтому при применении формулы Ньютона - Лейбница нужно строго следить за законностью этого действия.

Смысл формулы Ньютона - Лейбница (3.6) состоит в том, что для нахождения определённого интеграла   нам достаточно теперь найти произвольную первообразную   для функции   (напомним, что для этого надо найти неопределённый интеграл) и взять разность значений этой первообразной в концах отрезка,   .

Итак, формула Ньютона - Лейбница устанавливает связь между определённым интегралом от данной функции и первообразной для этой функции, то есть между определённым и неопределённым интегралами. Заметим, что смысл этих двух понятий первоначально совершенно различен: неопределённый интеграл -- это набор функций (первообразных), а определённый интеграл -- это число (равное пределу интегральных сумм).

При вычислениях разность   часто называют подстановкой в функцию   пределов   и   и обозначают 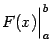  . Таким образом, по определению,

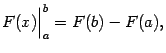
а формулу Ньютона - Лейбница можно записать в виде

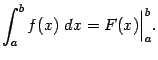
        Пример 3.1   Для нахождения значения определённого интеграла

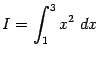
найдём первообразную для подынтегральной функции   , вычислив неопределённый интеграл:

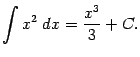
Поскольку нас интересует любая первообразная, то мы можем взять   (с тем же успехом могли взять и   , и   , и т.  п., но вид первообразной при   проще, а постоянные сласаемые всё равно взаимно уничтожатся при вычислении подстановки). Итак, берём   и вычисляем подстановку, беря в ней пределы равными пределам интегрирования:

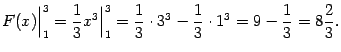
Получаем, что

    

        Пример 3.2   Найдём определённый интеграл

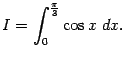
Поскольку

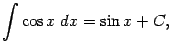
в качестве первообразной   можно взять   (положив   ). Поэтому