Вопрос 55. Интегрирование заменой переменной. Интегрирование методом подстановки.

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т. е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся (в случае «удачной» подстановки). Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

Пусть требуется вычислить интеграл . Сделаем подстановку – функция, имеющая непрерывную производную. Тогда и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой

(23.1)

Формула (23.1) также называется формулой замены переменных в неопределенном интеграле. После нахождения интеграла правой части этого равенства следует перейти от повой переменной интегрирования t назад к переменной х. Иногда целесообразно подбирать подстановку в виде ,тогда .Другими словами, формулу (23.1) можно применять справа налево.

56.Метод интегрирования по частям (с выводом)

57.Разложение рациональной функции на простейшие дроби.

Когда степень многочлена знаменателя дроби равна нулю (т.е. в знаменателе стоит число), дробь является многочленом. По теореме известно, что любой многочлен может быть разложен на множители.

Если степень знаменателя дроби больше нуля и степень числителя меньше степени знаменателя, то дробь можно представить в виде простейших дробей. Если степень числителя больше дроби знаменателя, то необходимо выполнить деление многочлена на многочлен «углом».

Пример. Разложить рациональную функцию на простейшие дроби.

.

Определим , , и из системы уравнений , . Итак, .

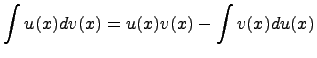
58.Разложение рациональной функции на простейшие дроби.

Для интегрирования рациональной функции , где P(x) и Q(x) - полиномы, используется следующая последовательность шагов:

Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;

Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;

Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициэнтов;

Вычислить интегралы от простейших дробей.

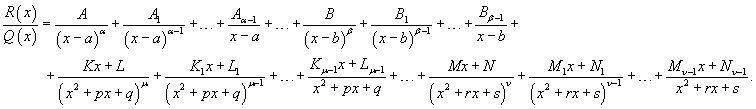
59.Интегрирование простейших иррациональностей. Подстановки Эйлера.

Рассмотрим случаи, в которых замена переменной позволяет интегралы от иррациональных функций свести к интегралам от рациональных функций.Обозначим через функцию от переменных и , и некоторых постоянных, которая построена с использованием лишь четырех арифметических действий (сложения, вычитания, умножения и деления). Например, , и т.д.

Интеграл вида , где рационализируется с помощью первой подстановки Эйлера .

Пример. Найти интеграл .

Здесь , поэтому применим подстановку . Возведем обе части равенства в квадрат , , приведем подобные члены, получим , откуда , .

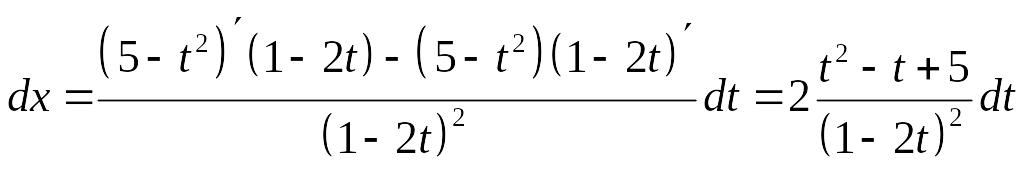Подставляя полученные выражения в данный интеграл, имеем

Интеграл вида , где рационализируется с помощью первой подстановки Эйлера .

Пример. Найти интеграл .

Здесь , поэтому применим подстановку . Возведем обе части равенства в квадрат , , приведем подобные члены, получим , откуда , , .

Подставляя полученные выражения в данный интеграл, имеем Разложим подынтегральную функцию на сумму простейших дробей: , откуда Полагая , находим , при , получим , при имеем , тогда .

Таким образом, получаем

Интеграл вида , где рационализируется с помощью первой подстановки Эйлера .

Пример. Вычислить .

Здесь , поэтому применим подстановку . Возведем обе части равенства в квадрат , , откуда , , .

Подставляя полученные выражения в интеграл, .