29.Предел функции. Непрерывность в точке, на интервале. Свойства.

Определение. Число называется пределом функции при , стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа , найдется такое положительное число (зависящее от ; ), что для всех таких, что , верно неравенство: .

Определение. Число называется пределом функции при , стремящемся к (или в точке ), если для любого, даже сколь угодно малого положительного числа , найдется такое положительное число (зависящее от ; ), что для всех , не равных и удовлетворяющих условию , выполняется неравенство: .

Теоремы о пределах:

Функция не может иметь более одного предела.

1. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е. .

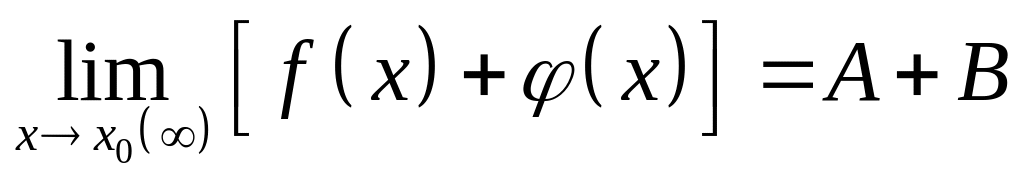2. Предел произведений конечного числа функций равен произведению пределов этих функций, т.е. .

3. Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.е. .

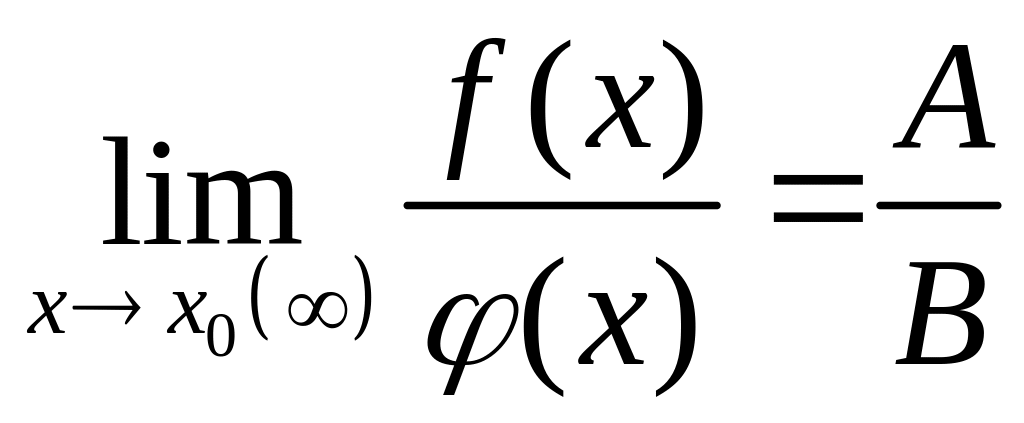
4. Если 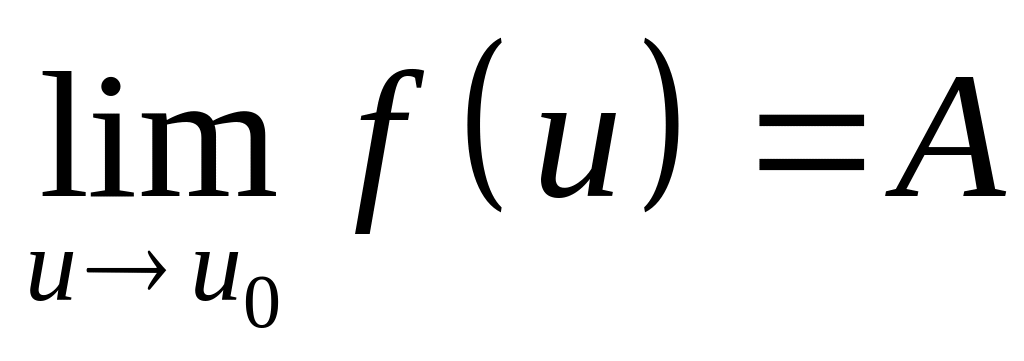, , 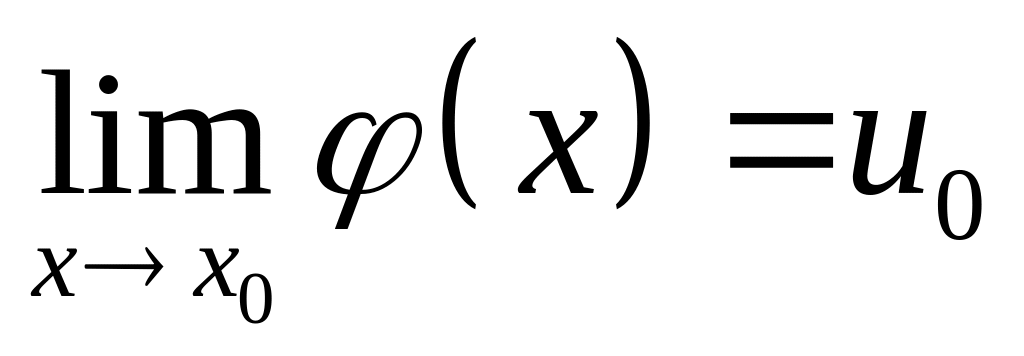то предел сложной функции .

5. Если в некоторой окрестности точки (или при достаточно больших ) 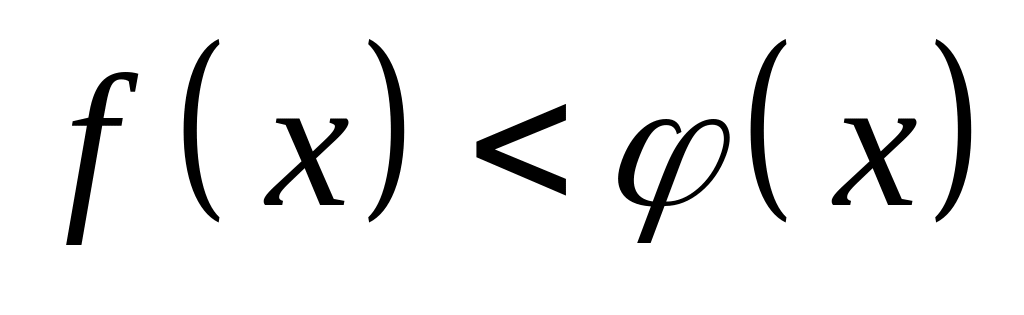, то .

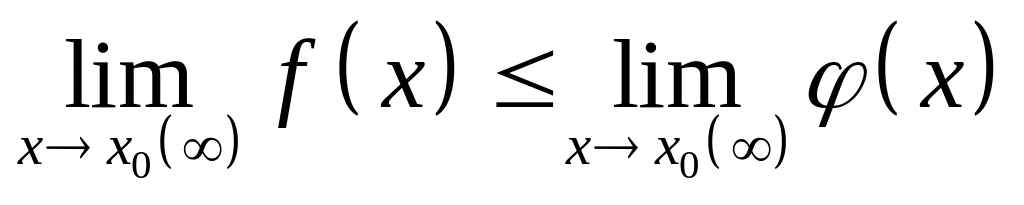Пример. Вычислить .

.

Определение. Функция называется непрерывной в точке , если она удовлетворяет следующим трем условиям: 1) определена в точке (т.е. существует ); 2) имеет конечный предел функции при ; 3) этот предел равен значению функции в точке , т.е. .

Свойства функций, непрерывных в точке:

1. Если функция и непрерывны в точке , то их сумма , произведение и частное (при условии ) являются функциями, непрерывными в точке .

2. Если функция непрерывны в точке и , то существует такая окрестность точки , в которой .

3. Если функция непрерывны в точке , а функция непрерывны в точке , то сложная функция непрерывна в точке .

Пример. Функция задана кусочно аналитически, различными аналитическими выражениями для различных подобластей изменения независимой переменной. Найти точки разрыва функции, если они существуют.

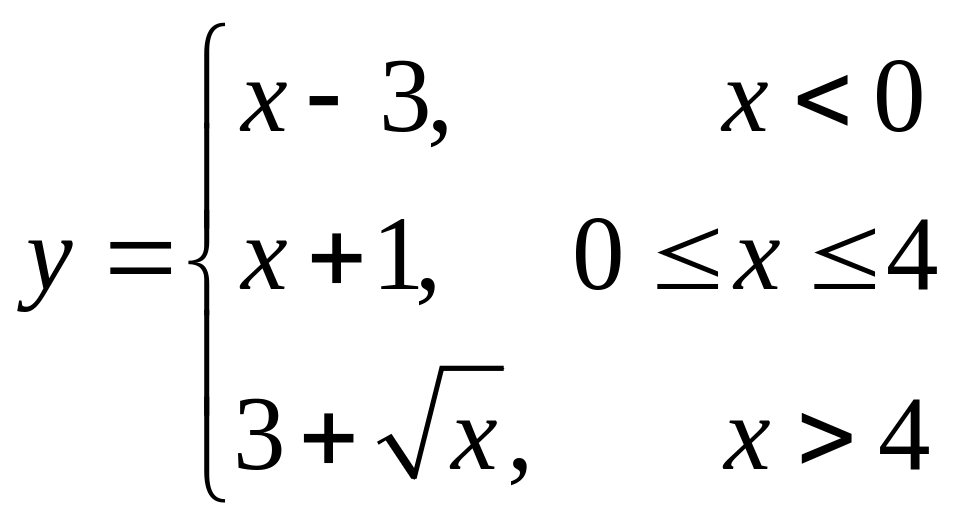
Так как , и , , т.е. , то в точке функция не является непрерывной.

Так как , и , , т.е. , то в точке функция непрерывна.

30 вопрос тоже.

Определение. Функция называется непрерывной на промежутке , если она непрерывна в каждой точке этого промежутка.

Свойства функций, непрерывных на отрезке:

1. Если функция непрерывна на отрезке , то она ограниченна на этом отрезке.

2. Если функция непрерывна на отрезке , то она достигает на этом отрезке наименьшего значения и наибольшего значения .

3. Если функция непрерывна на отрезке и значение ее на концах отрезка и имеют противоположные знаки, то внутри отрезка найдется точка такая, что .

Пример. Доказать непрерывность функции .

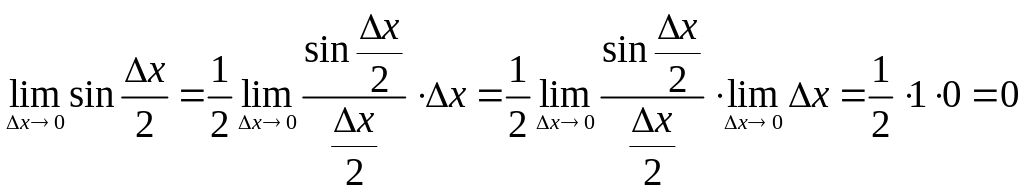Найдем . Так как , а , т.е. , то функция является непрерывной на всей числовой оси.

Вопрос 27. . Основные теоремы о пределах.

1. Бесконечно большие и бесконечно малые.

Функция f(x) стремится к бесконечности при x стремящимся к a, если для любого M > 0 можно указать такое значение  > 0, что для всех x удовлетворяющих неравенству xa < имеет место неравенство f(x) > M.

lim_x a=

2. Функция ограниченная при x a.

3. Функция ограниченная при x .

4. Теорема. Если lim_x a f(x)=b, то функция f(x) ограниченная при x a.

5. Бесконечно малые и их свойства. lim_x a (x)=0

Теорема. 1. Если f(x)=b+, где  - б.м. при x a, то lim_x a f(x)=b и обратно, если lim_x af(x)=b, то можно записать f(x)=b+(x).

Теорема. 2. Если lim_x a (x)=0 и (x)  0, то 1/ .

Теорема. 3. Сумма конечного числа б.м. есть б.м.

Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.

6. Теоремы о пределах.

Теорема. 1. Предел суммы есть сумма пределов.

Теорема. 2. Предел произведения есть произведение пределов.

Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).

Теорема. 4. Если u(x)  z(x)  v(x), и lim_x a u(x)=lim_x a v(x)=b, то lim_x a z(x)=b. ("Теорема о двух милиционерах").

7. 0.5sin(x) < 0.5x < 0.5tg(x)

   Первый замечательный предел.

8. lim x 0

   sin(x) x

   =1.

   Второй замечательный предел.

Переменная величина 

  1+ 1 n   n

при n  имеет предел, заключенный между 2 и 3.