
- •Вопрос 1. Определение множества
- •1.1.2. Операции над множествами
- •1.1.3. Свойства операций над множествами
- •1.2. Функции, их классификация
- •1.3. Предел последовательности
- •Вопрос4
- •Односторонние пределы. Необходимое и достаточное условия существования предела функции
- •Вопрос 6. Бесконечно малые и бесконечно большие функции
- •Вопрос 7. Теоремы о представлении функции в виде суммы предела и бесконечно малой функции
- •Вопрос8 Первый замечательный предел
- •Вопрос 9. Второй замечательный предел
- •1.8.3. Применение второго замечательного предела в финансовых вычислениях
- •Вопрос 10.Сравнение бесконечно малых функций
- •Вопрос 11.Непрерывность функции в точке и на отрезке.
- •Вопрос 12.Свойства непрерывных функций
- •Вопрос 13.Точки разрыва функций
- •Вопрос14.Определение производной функции
- •Дифференцируемость функции, ее взаимосвязь с производной и непрерывностью функции
- •Вопрос 16.Вывод производных основных элементарных функций
- •Правила дифференцирования
- •2.1.9. Производные высших порядков
- •Вопрос 20. Эластичность функции
- •2.1.11. Геометрический смысл эластичности
- •2.2.2. Геометрический смысл дифференциала
- •2.2.3. Свойства дифференциала
- •Вопрос 22. Применение дифференциала для приближенных вычислений
- •Вопрос 23.Теоремы о дифференцируемых функциях
- •2.3.1. Теорема Ролля
- •2.3.2. Геометрический смысл теоремы Ролля
- •2.3.3. Примеры использования теоремы Ролля
- •24. Теорема Лагранжа о конечном приращении функции
- •2.3.5. Геометрический смысл теоремы Лагранжа
- •2.3.6. Теорема Коши
- •2.3.7. Раскрытие неопределенностей при нахождении пределов. Правило Лопиталя
- •Вопрос 27. Формула Тейлора. Остаточный член в форме Лагранжа
- •Вопрос 28. Формула Маклорена
- •2.4.4. Применение формулы Маклорена для вычисления пределов и значений функций
- •2.5. Исследование функций
- •2.5.1. Необходимый и достаточный признаки монотонности функций
- •Вопрос 31. Определение экстремума функции
- •Вопрос 32.Первый достаточный признак экстремума функции (с использованием первой производной)
- •34. Необходимый признак существования точки перегиба
- •35.Асимптоты графика функции
- •2.5.11. Построение графика функции
- •3.4. Свойства пределов
- •38.Бесконечно малые функции нескольких переменных
- •47. . Производная функции по направлению
47. . Производная функции по направлению
Пусть
функция
 непрерывная и дифференцируемая, вектор
непрерывная и дифференцируемая, вектор
 задает направление. Пусть имеется точка
задает направление. Пусть имеется точка
 и в направлении
и в направлении
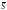 от нее точка
от нее точка


Вектор
 имеет координаты
имеет координаты
 ,
,
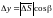 ,
,

 ,
,
 ,
,
 ,
,
 .
–направляющие
.
–направляющие




 .(формулы)
.(формулы)
48. Градиент функции, его свойства
Градиентом
функции
 называется
называется
 ,
,
един.векторы
един.векторы
Теорема
3.5. Производная
функции
 по направлению вектора
равняется проекции градиента этой
функции на это направление, т. е.
по направлению вектора
равняется проекции градиента этой
функции на это направление, т. е.
 .Проекция
некоторого вектора
.Проекция
некоторого вектора
 на направление вектора
на направление вектора
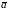 равняется
равняется
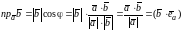 .
.
един.вектор, совп. по направлению с
.
един.вектор, совп. по направлению с
.

 .
.
Свойство
1. Производная
функции
 по направлению вектора
достигает своего наибольшего значения,
если направление вектора
совпадает с направлением градиента
этой функции.
по направлению вектора
достигает своего наибольшего значения,
если направление вектора
совпадает с направлением градиента
этой функции.
Свойство
2. Производная
функции
 по направлению вектора
равняется нулю, если направление вектора
перпендикулярно направлению градиента
этой функции.
по направлению вектора
равняется нулю, если направление вектора
перпендикулярно направлению градиента
этой функции.
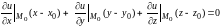 .
.
49. Формула Тейлора для функций двух переменных
Теорема
3.6. Если в
некоторой -окрестности
точки
 функция
функция
 непрерывна и имеет непрерывные
частные производные до (n1)-го
порядка включительно, то для любой точки
этой окрестности справедлива формула
непрерывна и имеет непрерывные
частные производные до (n1)-го
порядка включительно, то для любой точки
этой окрестности справедлива формула
 ,где
.
,где
.
Д о к а з а т е л ь с т в о. Формула Маклорена для функции одной переменной
 .
.
Новая функция
 .1
пр
.1
пр .
2пр.
.
2пр.
 ,
,
Запишем формулу Маклорена

 .
.
Учитывая,
что
 ,
формулу Маклорена можно записать в виде
,
формулу Маклорена можно записать в виде
 .
.
50.
Необходимый
признак локального экстремума.Теорема
3.7. Если точка
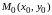 является точкой экстремума функции
является точкой экстремума функции
 ,
то частные производные в этой точке
либо равны ,либо
не существуют.
,
то частные производные в этой точке
либо равны ,либо
не существуют.
Д
о к-в о. Пусть точка
 является мочкой максимума функции
является мочкой максимума функции
 ,
т. е. сущ. -окрестность
этой точки
,
т. е. сущ. -окрестность
этой точки
 такая, что
такая, что

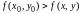 .
.
 в этой окрестности
в этой окрестности
 ,
поэтому точка
,
поэтому точка
 является также точкой максимума функции
является также точкой максимума функции
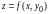 одной переменной х.
По необходимому признаку локального
экстремума функции одной переменной
производная в этой точке либо не
существует, либо равна нулю.
одной переменной х.
По необходимому признаку локального
экстремума функции одной переменной
производная в этой точке либо не
существует, либо равна нулю.
Достаточный признак локального экстремума функции двух переменных
Теорема
3.8. Если
функция
 в окрестности точки
в окрестности точки
 является непрерывной и имеет непрерывные
частные производные до второго порядка
включительно, и частные производные
первого порядка в этой точке равны нулю,
то:
является непрерывной и имеет непрерывные
частные производные до второго порядка
включительно, и частные производные
первого порядка в этой точке равны нулю,
то:
1)
если
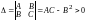 ,
,
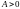 ,где
,где
 ,
,
 ,
,
 ,то
,то
 является т.мин ;2) если
является т.мин ;2) если
 ,
то
,
то
 является т.макс;3) если
является т.макс;3) если
 ,
то
не является т. экстр.4) если
,
то
не является т. экстр.4) если
 ,
то невозможно опред.
,
то невозможно опред.
Д о к-в о.Согласно формуле Тейлора пр
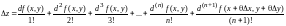 ,где
,где
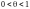 .
.
По
условию теоремы
 .
.
Дифф.
2 порядка .
.

 ;
; ,
т. е. лок. Мин. в точке
,
т. е. лок. Мин. в точке

 сл-но
сл-но
 .
.
Если

 ,
то
,
то
 .Тогда
точка
лок. макс Следовательно,
.Тогда
точка
лок. макс Следовательно,
 .
.
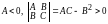 .
.
Если
 минор
второго порядка
минор
второго порядка
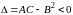 ,
,
Если
же
 ,
,
 в точке
в точке
 равен нулю, то доп.исследования
равен нулю, то доп.исследования
