Вопрос 36.Численное взятие производной.
Численное дифференцирование — совокупность методов вычисления значения производной дискретно заданной функции.
Введение
В основе численного дифференцирования лежит аппроксимация функции, от которой берется производная, интерполяционным многочленом. Все основные формулы численного дифференцирования могут быть получены при помощи первого интерполяционного многочлена Ньютона (формулы Ньютона для начала таблицы).
Основными задачами являются вычисление производной на краях таблицы и в ее середине. Для равномерной сетки формулы численного дифференцирования «в начале таблицы» можно представить в общем виде следующим образом:
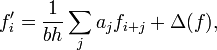
где 
—
погрешность формулы. Здесь
коэффициенты 
и 
зависят
от степени n использовавшегося
интерполяционного многочлена, то есть
от необходимой точности (скорости
сходимости к точному значению при
уменьшении шага сетки) формулы.
Коэффициенты представлены в таблице
Погрешность вычислений
Погрешность вычисляется по формуле
где 
—
шаг сетки, а точка 
расположена
где-то между 
-тым
и 
-тым
узлами. Примером может служить известная
формула 
.
При 
формула
может быть получена и из определения
производной. Эта формула известна под
названием формулы дифференцирования
вперед.
Формулы «в конце таблицы» могут быть представлены в общем виде
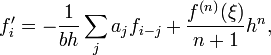
в которых коэффициенты берутся из уже приведенной таблицы. В частности, при получается известная формула дифференцирования назад.
Вопрос 37.Решение системы линейных уравнений методом Гаусса Метод Гаусса
Запишем систему Ax=f, в развернутом виде
Метод Гаусса состоит в последовательном
исключении неизвестных из этой системы.
Предположим, что
.
Последовательно умножая первое уравнение
на
и складывая с i-м
уравнение, исключим
из всех уравнений кроме первого. Получим
систему
Аналогичным
образом из полученной системы исключим
.
Последовательно, исключая все неизвестные,
получим систему треугольного вида
Описанная процедура называется прямым
ходом метода Гаусса. Заметим, что ее
выполнение было возможно при условии,
что все
,
не равны нулю.
Выполняя последовательные подстановки в последней системе, (начиная с последнего уравнения) можно получить все значения неизвестных.
.
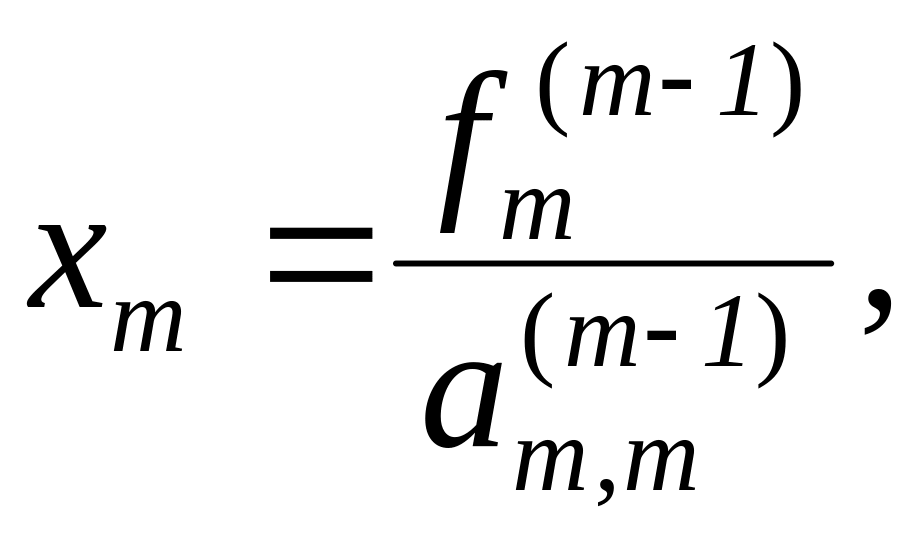
Эта процедура получила название обратный ход метода Гаусса. Метод Гаусса применим к любой системе линейных уравнений, он идеально подходит для решения систем, содержащих больше трех линейных уравнений.