Вопрос 24.Ортогональные функции и ортогональные полиномы

Две вещественные функции   и   на интервале   называются ортогональными, если

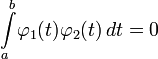
Для комплексных функций вводится комплексное сопряжение одной из функций под интегралом, для векторных — скалярное произведение функций под интегралом, а также интегрирование по отрезку заменяется на интегрирование по области соответствующей размерности.

Полезным обобщением понятия ортогональности является ортогональность с определённым весом. Ортогональны с весом   функции   и  , если

где   — скалярное произведение векторов   и   — значений векторнозначных функций   и   в точке  ,   — точка области  , а   — элемент её объёма (меры).

Пример

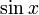1.  и 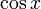  являются ортогональными функциями на интервале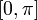 

В математике последовательностью ортогональных многочленов называют бесконечную последовательность действительных многочленов

,

где каждый многочлен   имеет степень  , а также любые два различных многочлена этой последовательностиортогональны друг другу в смысле некоторого скалярного произведения, заданного в пространстве  .

Многочлены Якоби

Многочлены Якоби обозначаются  , где параметры   и   вещественные числа больше −1. Если   и   не равны, полиномы перестают быть симметричными относительно точки  .

• Весовая функция 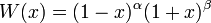  на промежутке ортогональности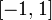 

Многочлены Чебышёва

Многочлен Чебышева   часто используется для аппроксимации функций как многочлен степени  , который меньше всего отклоняется от нуля на интервале 

Является частным случаем нормированного многочлена Гегенбауэра для параметра 

• Весовая функция 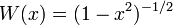  на промежутке ортогональности 

Вопрос 25.Построение полинома ортогонального на дискретной системе точек

Построение ортогональных многочленов

Процесс ортогонализации Грама-Шмидта

Система ортогональных многочленов   может быть построена путём применения процесса Грама-Шмидта к системе многочленов  следующим образом. Определим проектор как

,

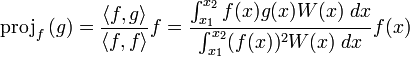тогда ортогональные полиномы последовательно вычисляются по схеме

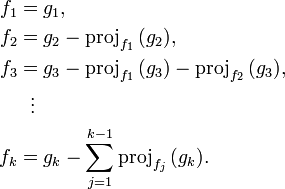
Данный алгоритм относится к численно неустойчивым алгоритмам. При вычислении коэффициентов разложения ошибки округления и погрешности численного интегрирования накапливаются с увеличением номера полинома.

По моментам весовой функции

Весовая функция  , заданная на промежутке  , однозначно определяет систему ортогональных многочленов   с точностью до постоянного множителя. Обозначим через числа

моменты весовой функции, тогда многочлен   может быть представлен в виде:

.

Сложность вычисления ортогональных полиномов определяется сложностью вычисления определителя матрицы. Существующие алгоритмические реализации вычисления требуют минимум   операций.

По рекуррентным формулам

Если выбрать нормировку многочлена   таким образом, что коэффициент   при главное члене равен единицы, рекуррентное соотношение может быть переписано в следующем виде:

где

.

Вопрос 26.Собственные векторы и собственные числа матрицы

Пусть дано линейное пространство R_n и действующий в нем линейный оператор A; в этом случае оператор A переводит R_n в себя, то есть A:R_n → R_n.

Определение. Ненулевой вектор   называется собственным вектором оператора A, если оператор A переводит   в коллинеарный ему вектор, то есть  . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору  .

Отметим некоторые свойства собственных чисел и собственных векторов.

1. Любая линейная комбинация собственных векторов   оператора A, отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.

2. Собственные векторы   оператора A с попарно различными собственными числами λ₁, λ₂, …, λ_m линейно независимы.

3. Если собственные числа λ₁=λ₂= λ_m= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.