57) Метод наискорейшего спуска

Метод наискорейшего спуска является одной из наиболее фундаментальных процедур минимизации дифференцируемой функции нескольких переменных. Вектор d называется направлением спуска для функции f в точке x, если существует такое d > 0, что f(x+lym*d)<f(x) для всех lym принадлежащих интервалу (0, d). В частности, если

Алгоритм метода наискорейшего спуска

При заданной точке x алгоритм наискорейшего спуска заключается в реализации линейного поиска вдоль направления или, что то же самое, вдоль направления -grad(f(x)).

Начальный этап. Пусть eps > 0 - константа остановки. Выбрать начальную точку , положить и перейти к основному этапу.

Основной этап. Если , то остановиться; в противном случае положить и найти - оптимальное решение задачи минимизации

при . Положить , заменить и повторить основной этап.

58) –––––

59) Решение систем нелинейных уравнений нескольких переменных методом Ньютона

В отличие от систем линейных уравнений для систем нелинейных уравнений не известны прямые методы решения. Лишь в отдельных случаях систему можно решить непосредственно. Например, для системы из двух уравнений иногда удается выразить одно неизвестное через другое и таким образом свести задачу к решению одного нелинейного уравнения относительно одного неизвестного. Поэтому итерационные методы для нелинейных систем приобретают особую актуальность.

Метод Ньютона.

Рассмотрим нелинейную систему уравнений

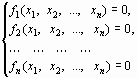(23)

или в векторной форме f (x) = 0, (23 ')

где

f

x

Для решения системы (23? ) будем пользоваться методом последовательных приближений.

Предположим, известно k-е приближение

одного из изолированных корней x = векторного уравнения (23 '). Тогда точный корень уравнения (23') можно представить в виде

где - поправка (погрешность корня).

Подставляя выражение (24) в (23'), будем иметь

(25)

Предполагая, что функция f (x) непрерывно дифференцируема в некоторой выпуклой области, содержащей x и x^(k), разложим левую часть уравнения (25) по степеням малого вектора D x^(k) , ограничиваясь линейными членами,

или, в развернутом виде,

(26)

Из формул (26) и (26') вытекает, что под производной f '(x) следует понимать матрицу Якоби системы функций f1, f2, ..., fn относительно переменных x1, x2, ..., xn, т. е.

f ' (x) = W(x) = ,

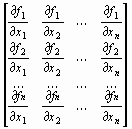или в краткой записи

f ' (x) = W(x) = (i, j = 1, 2, …, n).

Поэтому формула (26) может быть записана в следующем виде:

Если det W ( х ) = , то

Отсюда видно, что метод Ньютона решения системы (23) состоит в построении итерационной последовательности:

. (27)

Если все поправки становятся достаточно малыми, счет прекращается. Иначе новые значения используются как приближенные значения корней, и процесс повторяется до тех пор, пока не будет найдено решение или не станет ясно, что получить его не удастся.

Пример 9. Методом Ньютона приближенно найти положительное решение системы уравнений

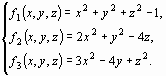
исходя из начального приближения .

Полагая:

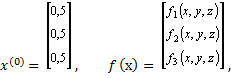
имеем:

f (х)=

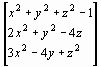
Отсюда

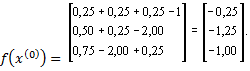
Составим матрицу Якоби

W(x) =

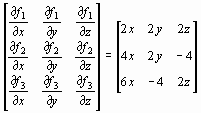
Имеем

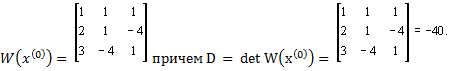
Следовательно, матрица - неособенная. Составим обратную ей матрицу

W -1 ( х(0) ) =

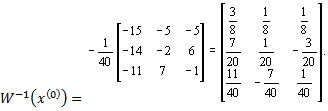
По формуле (27) получаем первое приближение

х(1) = x(0) - W -1(x(0) ) f (x(0) ) = - = + = .

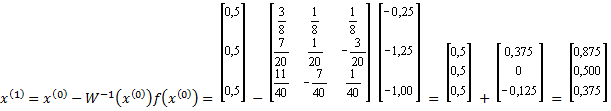
Аналогично находятся дальнейшие приближения. Результаты вычислений приведены в Таблице 3.

Таблица 3

i	x	y	z
0	0,5	0,5	0,5
1	0,875	0,5	0,375
2	0,78981	0,49662	0,36993
3	0,78521	0,49662	0,36992

Останавливаясь на приближении , будем иметь:

x = 0,7852; y = 0,4966; z =0,3699.