Различные формы остаточного члена
В форме Лагранжа:
В форме Коши:
В интегральной форме:
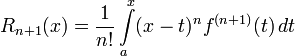
Вопрос 34.Минимизация погрешности интерполяции
В
некоторых случаях удается улучшить
результаты глобальной интерполяции за
счет специального расположения узлов
интерполяции (если они не зафиксированы).
Доказано, что если функция 
имеет
непрерывную производную на отрезке 
,
то при выборе значений 
,
совпадающих с корнями полинома Чебышева
степени n,
интерполяционные полиномы степени n-1
сходятся к значениям функции в любой
точке этого отрезка. Корни многочлена
Чебышева на отрезке
определяются
выражением
, 
.
Они расположены неравномерно на отрезке и сгущаются к его концам. Такое сгущение компенсирует увеличение погрешности интерполяции при приближении к концам отрезка, которое имеет место при равномерном расположении узлов.
Однако не всегда удается выбрать такое специальное расположение узлов, которое обеспечивает хорошую точность глобальной интерполяции. В тех случаях, когда узлы интерполяции фиксированы, уменьшение погрешности интерполяции осуществляют за счет уменьшения степени интерполяционных полиномов, применяя многоинтервальную интерполяцию.
Вопрос 35.Обобщенный подход к процессу интерполяции Интерполяция функций интерполяционными полиномами
В вычислительной математике существенную роль играет интерполяция функций, т.е. построение по заданной функции другой (как правило, более простой), значения которой совпадают со значениями заданной функции в некотором числе точек. Причем интерполяция имеет как практическое, так и теоретическое значение. На практике часто возникает задача о восстановлении непрерывной функции по ее табличным значениям, например полученным в ходе некоторого эксперимента. Для вычисления многих функций оказывается эффективно приблизить их полиномами или дробно-рациональными функциями (см., например [1] Ссылка в списке литературы). Теория интерполирования используется при построении и исследовании квадратурных формул для численного интегрирования, для получения методов решения дифференциальных и интегральных уравнений.
Все перечисленные выше вопросы рассмотрены в классических учебниках по численным методам (см., например, [2-5] Ссылки в списке литературы). Цель этого раздела - демонстрация возможностей MATLAB для изучения вопросов, возникающих при интерполяции функций, в основном при помощи интерполяционных полиномов. В данном разделе приводятся необходимые сведения об интерполяции функций и при помощи небольших программ, написанных на языке пакета MATLAB, изучаются проблемы, возникающие при интерполяции функций. Простота языка пакета MATLAB в сочетании с широким набором его функций, в том числе и графических, позволяет вместо написания собственных программ интерполяции и визуализации результатов сосредоточиться на исследовании большого числа примеров, что может быть использовано при проведении лабораторных работ по численным методам для студентов технических факультетов вузов и институтов.
Задача интерполяции функции, интерполяционные полиномы
Пусть на отрезке [a,b] задана функция ƒ(x). Задача интерполяции (или интерполирования) состоит в построении функции g(x), совпадающей с заданной ƒ(x) в некотором наборе точек {x1,x2,...,xn+1} из отрезка [a,b] (эти точки называются узлами интерполяции), т.е. должны выполняться условия:
g(xk)=yk, k=1,2,...,n+1,
где yk - известные значения функции ƒ(x) в точках xk. Функция g(x) называется интерполянтом функции ƒ(x).
Важно, что какие бы подходы для построения интерполяционного полинома не применялись, они всегда должны привести к одинаковому результату (если все вычисления проводятся точно, а не на компьютере), поскольку интерполяционный полином степени существует и единственный при различных -ом узлах интерполяции. Другое дело, что разные способы построения интерполяционного полинома могут обладать разными вычислительными свойствами. Рассмотрим сначала интерполяционный полином в форме Лагранжа. Далее мы будем использовать обозначение для интерполяционного полинома в зависимости от способа его построения.