Вопрос 21.Ортогональная, ортонормированная матрица, неквадратная матрица с ортогональными (ортонормированными) столбцами.

Ортогональная матрица — квадратная матрица A с вещественными элементами, результат умножения которой на A^T равен единичной матрице:^[1]

или, что эквивалентно, её обратная матрица равна транспонированной матрице:

Матрица, столбцы и строки которой образуют системы ортонормированных векторов. Другими словами, скалярное произведение строки на саму себя равно 1, а на любую другую строку — 0. Так же и для столбцов.

Вопрос 22.Обращение матрицы методом Гаусса

Метод Гаусса — Жордана (метод полного исключения неизвестных) — метод, который используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе или отыскания ранга матрицы.

Алгоритм

1. Выбирают первый слева столбец матрицы, в котором есть хоть одно отличное от нуля значение.

2. Если самое верхнее число в этом столбце есть ноль, то меняют всю первую строку матрицы с другой строкой матрицы, где в этой колонке нет нуля.

3. Все элементы первой строки делят на верхний элемент выбранного столбца.

4. Из оставшихся строк вычитают первую строку, умноженную на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) ноль.

5. Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.

6. После повторения этой процедуры 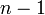  раз получают верхнюю треугольную матрицу

7. Вычитаем из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали.

8. Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).

9. Чтобы получить обратную матрицу, нужно применить все операции в том же порядке к единичной матрице.

Пример

Для решения следующей системы уравнений:

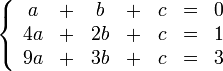
Запишем её в виде матрицы 3×4, где последний столбец является свободным членом:

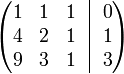
Проведём следующие действия:

• К строке 2 добавим: −4 × Строку 1.

• К строке 3 добавим: −9 × Строку 1.

Получим:

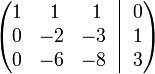
• К строке 3 добавим: −3 × Строку 2.

• Строку 2 делим на −2

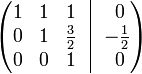
• К строке 1 добавим: −1 × Строку 3.

• К строке 2 добавим: −3/2 × Строку 3.

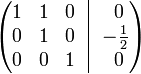
• К строке 1 добавим: −1 × Строку 2.

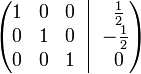
В правом столбце получаем решение:

 .

Вопрос 23.Разложение матрицы в произведение ортогональной и треугольной (метод Шмидта)

Преобразуем матрицу А в ортонормированную матрицу, и затем представим ее в виде последовательности векторов (столбцы по порядку). Определим первый вектор столбец ортогональной матрицы r1 из соотношения

r1=a1

Для определения второго вектор столбца r2 ортогональной матрицы воспользуемся

выражением, где t1,2 неопределенный пока коэффициент

a2 r2+ t1 2 *r1

Положим далее, что

tii= 1

и принимая во внимание, что векторы r2 и r1 ортогональны для определения

коэффициента t1,2 получим выражение

t_1,2=(a₂^Т*r1)/(r1^T*r1)

где через x^Ty – обозначено скалярное произведение векторов.

Найдя все вектора получим ортогональную матрицу, затем нормируем ее (умножая ортогональную матрицу, на диагональную матрицу норм)

Разложение матрицы в произведение ортонормированной и треугольной Е*Т

A=Rt=E*D^-1*Dt T=Dt При проверке должно получиться E*T=A=R*t