53) Метод золотого сечения

Метод золотого сечения — метод поиска значений действительно-значной функции на заданном отрезке. В основе метода лежит принцип деления в пропорциях золотого сечения. Наиболее широко известен как метод поиска экстремума в решении задач оптимизации.

Пусть задана функция . Тогда для того, чтобы найти определённое значение этой функции на заданном отрезке, отвечающее критерию поиска (пусть это будет минимум), рассматриваемый отрезок делится в пропорции золотого сечения в обоих направлениях, то есть выбираются две точки и такие, что:

, где — пропорция золотого сечения.

Таким образом:

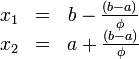
То есть точка делит отрезок в отношении золотого сечения. Аналогично делит отрезок в той же пропорции. Это свойство и используется для построения итеративного процесса.

Алгоритм

1) На первой итерации заданный отрезок делится двумя симметричными относительно его центра точками и рассчитываются значения в этих точках.

2) После чего тот из концов отрезка, к которому среди двух вновь поставленных точек ближе оказалась та, значение в которой максимально (для случая поиска минимума), отбрасывают.

3) На следующей итерации в силу показанного выше свойства золотого сечения уже надо искать всего одну новую точку.

4) Процедура продолжается до тех пор, пока не будет достигнута заданная точность.

Формализация

Шаг 1. Задаются начальные границы отрезка и точность .

Шаг 2. Рассчитывают начальные точки деления: и значения в них целевой функции: .

Если (для поиска max изменить неравенство на ), то .

Иначе .

Шаг 3. Если , то и останов. Иначе возврат к шагу 2.

54, 55) –––

56) Симплекс метод (метод Нелдера – Мида)

Метод Нелдера — Мида, также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий производной (точнее — градиентов) функции, а поэтому легко применим к негладким и/или зашумлённым функциям.

Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума.

Метод находит локальный экстремум и может «застрять» в одном из них. Если всё же требуется найти глобальный экстремум, можно пробовать выбирать другой начальный симплекс. Более развитый подход к исключению локальных экстремумов предлагается в алгоритмах, основанных на методе Монте-Карло, а также в эволюционных алгоритмах.

Алгоритм

Пусть требуется найти безусловный минимум функции n переменных . Предполагается, что серьёзных ограничений на область определения функции нет, то есть функция определена во всех встречающихся точках.

Параметрами метода являются:

• коэффициент отражения 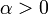, обычно выбирается равным .

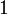• коэффициент сжатия 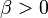, обычно выбирается равным .

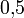• коэффициент растяжения 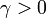, обычно выбирается равным .

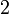1) «Подготовка». Вначале выбирается точка , образующие симплекс n-мерного пространства. В этих точках вычисляются значения функции: .

2) «Сортировка». Из вершин симплекса выбираем три точки: с наибольшим (из выбранных) значением функции , со следующим по величине значением и с наименьшим значением функции . Целью дальнейших манипуляций будет уменьшение по крайней мере .

3) Найдём центр тяжести всех точек, за исключением

Вычислять не обязательно.

4) «Отражение». Отразим точку относительно с коэффициентом (при это будет центральная симметрия, в общем случае — гомотетия), получим точку и вычислим в ней функцию: . Координаты новой точки вычисляются по формуле:

.

5) Далее смотрим, насколько нам удалось уменьшить функцию, ищем место в ряду .

• Если 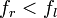, то направление выбрано удачное и можно попробовать увеличить шаг. Производим «растяжение». Новая точка 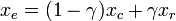и значение функции .

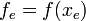• Если 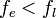, то можно расширить симплекс до этой точки: присваиваем точке значение 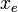и заканчиваем итерацию (на шаг 9).

• Если 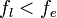, то переместились слишком далеко: присваиваем точке значение и заканчиваем итерацию (на шаг 9).

• Если , то выбор точки неплохой (новая лучше двух прежних). Присваиваем точке значение и переходим на шаг 9.

• Если 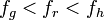, то меняем местами значения и . Также нужно поменять местами значения и . После этого идём на шаг 6.

• Если 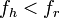, то просто идём на следующий шаг 6.

В результате (возможно, после переобозначения) .

6) «Сжатие». Строим точку и вычисляем в ней значение .

7) Если , то присваиваем точке значение и идём на шаг 9.

8) Если , то первоначальные точки оказались самыми удачными. Делаем «глобальное сжатие» симплекса — гомотетию к точке с наименьшим значением

: , .

9) Последний шаг — проверка сходимости. Может выполняться по-разному, например, оценкой дисперсии набора точек. Суть проверки заключается в том, чтобы проверить взаимную близость полученных вершин симплекса, что предполагает и близость их к искомому минимуму. Если требуемая точность ещё не достигнута, можно продолжить итерации с шага 2.