Вопрос №1: (Матрицы. Линейные операции в множестве матриц. Их свойства. Понятие линейного пространства)

Матрица – прямоугольная таблица чисел, содержащая 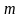строк и 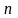столбцов, записанная в круглых скобках или двойных прямых чертах. Если = – матрица квадратная. Если =1 – матрица – строка. Если =1 – матрица – столбец. Если в матрице все элементы, стоящие ниже главной диагонали равны 0, то такая матрица – верхняя треугольная. Если в матрице все элементы, стоящие выше главной диагонали равны 0, то такая матрица – нижняя треугольная. Все числа, входящие в матрицу называются ее элемен­тами.

Если все элементы состоят их нулей, то это нулевая матрица, она играет роль нуля в матричном исчислении.

Две матрица считаются равными, если они одинакового размера и их соответствующие элементы совпадают.

Линейные операции в множестве матриц.

• Сложение матриц.

Суммой двух матриц одинаковой размерности, называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых.( 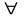А и В, принадлежащих R^mxn) Полученная матрица, также принадлежит R^mxn.

• Умножение матрицы на число.

По определению, чтобы умножить матрицу на число, нужно умножить на это число все элементы матрицы. 

( А, принадлежащего R^mxn. α принадлежащего R) Полученная в результате матрица, также принадлежит R^mxn.

Свойства сложения матриц и умножения на число:

1) A+B=B+A, А и В принадлежащим R^mxn (Комутотивность)

2) (А+В)+С = А+(В+С), А, В и С принадлежащим R^mxn (Ассоциативность)

3) Существует такая нулевая матрица, принадлежащая R^mxn, такая что

О+А = А+О = А, А, принадлежащего R^mxn (Наличие нейтрального относительного сложения элементов)

4) А, принадлежащего R^mxn существует (-А),

принадлежащая R^mxn, такая что (-А)+А = А+(-А) = О

5) 1*А = А, А, принадлежащего R^mxn, 1 принадлежит R.

6) (α*β)*А = α*(β*А), А, принадлежащего R^mxn. Для любого

α и β, принадлежащих R.

7) α*(А+В) = α*А+ α*В, А и В, принадлежащих R^mxn. Для любого α и β, принадлежащих R.

8) (α+β)*А = α*А+β*А А, принадлежащего R^mxn. Для любого α и β, принадлежащих R.

Доказательство:

1) Свойства 1,2,5,6,7,8 верны для R, сложение и умножение определены по элементарным преобразованиям.

2) Свойство 3 выполняется в качестве нейтрального элемента. В качестве нейтрального элемента берется матрица, равная нулю.

3) Свойство 4 выполняется, так как для матрицы А существует матрица (-А) с противоположными А элементами.

Понятие линейного пространства.

Определение:

Множество V с введенными на нем линейными

операциями сложениями и умножением на число, обладающими свойствами 1-8, называется – линейным векторным пространством, таким образом, свойства 1-8, утверждают, что R^mxnявляется линейным пространством.

В любом линейном пространстве можно сконструировать разность, которая выглядит: А-В = А+(-1)*В, где А и В принадлежат V.

В любом линейном пространстве существует линейный комбинатор.

Определение:

Линейный комбинатор – это комбинатор элементов А₁,……..,А_к , принадлежащих V с коэфицентами α₁,…….,α_к, принадлежащих R, называется выражение: α₁ А₁+ α₂ А₂+….+ α_к А_к принадлежащих множеству V.