
- •1)Векторное (линейное) пространство - математическое понятие, обобщающее понятие совокупности всех (свободных) векторов обычного трехмерного пространства.
- •Вопрос 21.Ортогональная, ортонормированная матрица, неквадратная матрица с ортогональными (ортонормированными) столбцами.
- •Вопрос 22.Обращение матрицы методом Гаусса
- •Вопрос 23.Разложение матрицы в произведение ортогональной и треугольной (метод Шмидта)
- •Вопрос 24.Ортогональные функции и ортогональные полиномы
- •Вопрос 25.Построение полинома ортогонального на дискретной системе точек
- •По моментам весовой функции
- •По рекуррентным формулам
- •Вопрос 26.Собственные векторы и собственные числа матрицы
- •Вопрос 27.Матрица простой структуры, ее свойства
- •Вопрос 28.Сингулярное разложение
- •Вопрос 29.Нормы векторов и матриц Норма вектора
- •Норма матрицы
- •Вопрос 30.Метрическое векторное пространство
- •Вопрос 32.Градиент, свойства градиента
- •Вопрос 33.Матричная форма записи ряда Тейлора. Формула Тейлора
- •Различные формы остаточного члена
- •Вопрос 34.Минимизация погрешности интерполяции
- •Вопрос 35.Обобщенный подход к процессу интерполяции Интерполяция функций интерполяционными полиномами
- •Задача интерполяции функции, интерполяционные полиномы
- •Вопрос 36.Численное взятие производной.
- •Введение
- •Погрешность вычислений
- •Вопрос 37.Решение системы линейных уравнений методом Гаусса Метод Гаусса
- •Вопрос 38.Матрица перестановок
- •Определение
- •Свойства
- •Вопрос 39.Решение системы линейных алгебраических уравнений методом Гаусса с выбором главного элемента по столбцам Метод Гаусса с выбором главного элемента
- •Вопрос 40.Решение системы линейных алгебраических уравнений методом вращения Метод вращения
- •40.Решение системы линейных алгебраических уравнений методом вращения
- •41.Решение системы линейных уравнений методом факторизации матрицы
- •42.Итерационный процесс решения систем линейных алгебраических уравнений
- •43.Функции невязки, ошибок
- •44.Метод простой итерации
- •45.Итерационный метод смещения
- •Пример.
- •46) Метод Якоби
- •47) Метод Зейделя
- •48) Метод релаксации Метод релаксации - итерационный метод решения систем линейных уравнений.
- •49) Метод Чебышева
- •50/51) Метод минимальных невязок (Одношаговый, двухшаговый - гугл не нашел )
- •52) Решение нелинейного уравнения одной переменной методом дихотомии
- •53) Метод золотого сечения
- •56) Симплекс метод (метод Нелдера – Мида)
- •57) Метод наискорейшего спуска
- •59) Решение систем нелинейных уравнений нескольких переменных методом Ньютона
- •60.Решение нелинейного уравнения нескольких переменных методом Левенберга - Марквардта
- •61.Решение системы нелинейных уравнений методом спуска
- •62.Решение системы нелинейных уравнений методом Ньютона
- •63.Решение системы нелинейных уравнений методом Левенберга - Марквардта
- •64.Структура м – функции
- •65.Арифметические операторы Матлаб
- •65)Арифметические операторы.
Вопрос 27.Матрица простой структуры, ее свойства
Линейный оператор называется оператором простой структуры, если существует базис, состоящий из собственных векторов этого оператора. Матрица простой структуры-это матрица этого оператора, в ней по диагонали стоят собственные числа.Матрицей простой структуры называются матрицы, которые с помощью преобразования подобия можно привести к диагональному виду. Теорема 4.2. Матрица А является матрицей простой структуры тогда и только тогда, когда она имеет n линейно независимых собственных векторов e1, e2,…, en, отвечающих собственным значениям λ λ λn, ,... 1 2соответственно.
Теорема 4.3. Если все собственные значения матрицы А различны, то она является матрицей простой структуры.
Теорема 4.4. Если А-вещественная симметричная матрица, то она подобна диагональной матрице, причем матрица подобия Р может быть выбрана ортогональной (т.е. удовлетворяющей условию P-1=PТ).
Вопрос 28.Сингулярное разложение
Сингуля́рное
разложе́ние (англ. singular
value decomposition, SVD) —
это разложение прямоугольной вещественной или комплексной матрицы,
применяющееся во многих областях
прикладной математики. Сингулярное
разложение может быть использовано,
например, для
нахождения ранга и ядра матриц, псевдообратных
матриц,
приближения матриц матрицами заданного
ранга.
Любая матрица ![]() порядка
порядка ![]() ,
элементы которой — комплексные
числа,
может быть представлена в следующем
виде, называемом сингулярным
разложениемматрицы
:
,
элементы которой — комплексные
числа,
может быть представлена в следующем
виде, называемом сингулярным
разложениемматрицы
:
![]()
где ![]() — унитарная
матрица порядка
— унитарная
матрица порядка ![]() ,
, ![]() — диагональная
матрица порядка
с
неотрицательными вещественными числами
на диагонали,
— диагональная
матрица порядка
с
неотрицательными вещественными числами
на диагонали, ![]() —
унитарная матрица порядка
—
унитарная матрица порядка ![]() ,
а
,
а ![]() — сопряжённо-транспонированная
матрица к
.
— сопряжённо-транспонированная
матрица к
.
Под диагональной прямоугольной матрицей здесь понимается матрица такая, что все её недиагональные элементы равны нулю:
![]() если
если ![]()
В
частном случае, когда
состоит
из вещественных
чисел,
существует сингулярное разложение
вида ![]() ,
в котором
и
— ортогональные
матрицы.
,
в котором
и
— ортогональные
матрицы.
Элементы ![]() на
диагонали матрицы
называются сингулярными
числами матрицы
и
определены с точностью до их перестановки.
Обычно требуют, чтобы они располагались
в матрице
в
невозрастающем порядке — тогда
(но
не
и
)
однозначно определяется по матрице
.
Столбцы матриц
и
называются,
соответственно, левыми и правыми сингулярными
векторами.
на
диагонали матрицы
называются сингулярными
числами матрицы
и
определены с точностью до их перестановки.
Обычно требуют, чтобы они располагались
в матрице
в
невозрастающем порядке — тогда
(но
не
и
)
однозначно определяется по матрице
.
Столбцы матриц
и
называются,
соответственно, левыми и правыми сингулярными
векторами.
Пусть дана матрица:
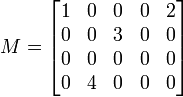
Одним
из сингулярных разложений этой матрицы
является разложение ![]() ,
где матрицы
,
и
следующие:
,
где матрицы
,
и
следующие:
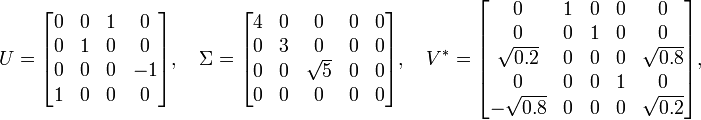
так
как матрицы
и
унитарны (![]() и
и ![]() ,
где
,
где ![]() — единичная
матрица),
а
—
прямоугольная диагональная
матрица,
то есть
— единичная
матрица),
а
—
прямоугольная диагональная
матрица,
то есть ![]() ,
если
,
если ![]() .
.
Вопрос 29.Нормы векторов и матриц Норма вектора
Норма
в векторном
пространстве
над полем вещественных или комплексных
чисел —
это функционал ![]() ,
обладающий следующими свойствами:
,
обладающий следующими свойствами:
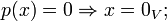
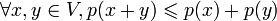 (неравенство
треугольника);
(неравенство
треугольника);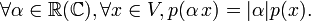
Эти условия являются аксиомами нормы.
Векторное пространство с нормой называется нормированным пространством, а условия (1-3) — также аксиомами нормированного пространства.
Нетрудно видеть, что из аксиом нормы вытекает свойство неотрицательности нормы:
4. ![]()
Действительно:
Из
3 получаем, что ![]() .
Теперь из 2 получаем
.
Теперь из 2 получаем ![]() .
Таким образом,
.
Таким образом, ![]() .
.
Чаще
всего норму обозначают в виде: ![]() .
В частности,
.
В частности, ![]() —
это норма элемента
векторного
пространства
—
это норма элемента
векторного
пространства ![]() .
.
Вектор
с единичной нормой (![]() )
называется нормальным или нормированным.
)
называется нормальным или нормированным.
Любой
ненулевой вектор
можно нормировать,
то есть разделить его на свою норму:
вектор ![]() имеет
единичную норму. С геометрической точки
зрения это значит, что мы берем
сонаправленный вектор единичной длины.
имеет
единичную норму. С геометрической точки
зрения это значит, что мы берем
сонаправленный вектор единичной длины.
