
- •События, их виды и действия с ними. Алгебра событий. Аксиоматическое определение вероятности.
- •Аксиоматическое определение вероятности
- •Классическое и статистическое определения вероятности. Свойства вероятности. Классическое определение вероятности.
- •Свойства вероятности.
- •Относительная частота. Статистическое определение вероятности.
- •Теоремы сложения вероятностей. Теорема сложения вероятностей.
- •4. Независимость событий. Условные вероятности. Теоремы об умножениях вероятностей зависимых и независимых событий. Условная вероятность
- •Независимость событий
- •Теоремы умножения вероятностей.
- •5. Формула полной вероятности. Формулы Байеса. Формула полной вероятности.
- •6. Схема и формула Бернулли.
- •7. Понятия случайной величины.
- •Функция распределения
- •Свойства функции распределения:
- •Числовые характеристики дискретной случайной величины.
- •Свойства математического ожидания:
- •Свойства дисперсии:
- •8. Математическое ожидание св и его свойства.
- •Дисперсия и ее свойства. Стандартное отклонение.
- •Свойства дисперсии:
- •10. Биномиальное распределение. Формула Бернулли. Распределение Пуассона. Биномиальное распределение
- •Распределение Пуассона
- •11. Непрерывная случайная величина
- •Свойства функции распределения:
- •Плотность распределения вероятностей и ее свойства.
- •Свойства плотности распределения вероятностей:
- •13. Равномерный закон распределения
- •Понятие многомерной (векторной) св и ее закон, функция и плотность распределения. Условные математические ожидания и дисперсии. Многомерные случайные величины
- •Зависимые св. Ковариация и коэффициент корреляции. Корреляционная матрица случайного вектора. Независимые случайные величины
- •Свойства независимых случайных величин
- •Ковариация
- •Линейный коэффициент корреляции
- •Нормальное распределение.
- •Центральная предельная теорема
- •Нормальное распределение(не википед)
- •18. Вероятность попадания св в заданный интервал .Вероятность заданного отклонения нормальной св.Правило 3 сигм.
- •Отметим ряд свойств функции Лапласа, полезных для применения.
- •19. Теоремы Муавра-Лапласа
- •Понятие о центральной предельной теореме Ляпунова и ее применение.
- •Задачи математической статистики. Генеральная и выборочная совокупности.
- •Статистическое распределение. Эмпирическая функция распределения и ее свойства.
- •Полигон и гистограмма.
- •Генеральная и выборочная средние, их свойства. Оценка генеральной средней по выборочной.
- •Генеральная и выборочная дисперсии, их свойства. Оценка генеральной дисперсии по выборочной. Исправленная дисперсия.
- •Линейная регрессия. Метод наименьших квадратов.
Зависимые св. Ковариация и коэффициент корреляции. Корреляционная матрица случайного вектора. Независимые случайные величины
Определение .
Пусть дано семейство случайных величин
![]() ,
так что
,
так что
![]() .
Тогда эти случайные величины попарно
независимы, если попарно независимы
порождённые ими сигма-алгебры
.
Тогда эти случайные величины попарно
независимы, если попарно независимы
порождённые ими сигма-алгебры
![]() .
Случайные величины независимы в
совокупности, если таковы порождённые
ими сигма-алгебры.
.
Случайные величины независимы в
совокупности, если таковы порождённые
ими сигма-алгебры.
Определение, данное
выше, эквивалентно любому другому из
нижеперечисленных. Две случайные
величины
![]() независимы
тогда и только тогда, когда:
независимы
тогда и только тогда, когда:
Для любых
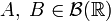 :
:
![]()
Для любых борелевских функций
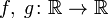 случайные
величины
случайные
величины
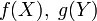 независимы.
независимы.Для любых ограниченных борелевских функций :
![]()
Свойства независимых случайных величин
Пусть
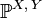 —
распределение случайного вектора
—
распределение случайного вектора
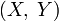 ,
,
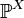 —
распределение
—
распределение
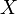 и
и
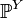 —
распределение
—
распределение
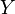 .
Тогда
независимы
тогда и только тогда, когда
.
Тогда
независимы
тогда и только тогда, когда
![]()
где
![]() обозначает
(прямое) произведение мер.
обозначает
(прямое) произведение мер.
Пусть
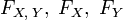 —
кумулятивные функции распределения
—
кумулятивные функции распределения
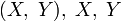 соответственно.
Тогда
независимы
тогда и только тогда, когда
соответственно.
Тогда
независимы
тогда и только тогда, когда
![]()
Пусть случайные величины дискретны. Тогда они независимы тогда и только тогда, когда
![]()
Пусть случайные величины совместно абсолютно непрерывны, то есть их совместное распределение имеет плотность
 .
Тогда они независимы тогда и только
тогда, когда
.
Тогда они независимы тогда и только
тогда, когда
![]() ,
,
где
![]() —
плотности случайных величин
и
соответственно.
—
плотности случайных величин
и
соответственно.
Ковариация
Важной характеристикой совместного распределения двух случайных величин является ковариация (или корреляционный момент). Ковариация являетcя совместным центральным моментом второго порядка. Ковариация определяется как математическое ожидание произведения отклонений случайных величин:
![]() ,
,
где
![]() —
математическое ожидание.
—
математическое ожидание.
Свойства ковариации:
Ковариация двух независимых случайных величин
 и
и
 равна
нулю.
равна
нулю.
Доказательство:
Так
как
и
—
независимые случайные величины, то и
их отклонения
![]() и
и
![]() также
независимы. Пользуясь тем, что
математическое ожидание произведения
независимых случайных величин равно
произведению математических ожиданий
сомножителей, а математическое ожидание
отклонения равно нулю, имеем
также
независимы. Пользуясь тем, что
математическое ожидание произведения
независимых случайных величин равно
произведению математических ожиданий
сомножителей, а математическое ожидание
отклонения равно нулю, имеем
![]()
Абсолютная величина ковариации двух случайных величин и не превышает среднего геометрического их дисперсий:
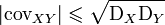 .
.
Доказательство:
Введём
в рассмотрение случайную величину
![]() (где
(где
![]() —
среднеквадратическое отклонение) и
найдём её дисперсию
—
среднеквадратическое отклонение) и
найдём её дисперсию
![]() .
Выполнив выкладки получим:
.
Выполнив выкладки получим:
![]()
Любая дисперсия неотрицательна, поэтому
![]()
Отсюда
![]()
Введя
случайную величину
![]() ,
аналогично
,
аналогично
![]()
Объединив полученные неравенства имеем
![]()
Или
![]()
Итак,
![]()
Ковариация имеет размерность, равную произведению размерности случайных величин, то есть величина ковариации зависит от единиц измерения независимых величин. Данная особенность ковариации затрудняет её использование в целях корреляционного анализа.
Линейный коэффициент корреляции
Для устранения недостатка ковариации был введён линейный коэффициент корреляции Коэффициент корреляции рассчитывается по формуле:

Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы.
Доказательство:
Разделив
обе части двойного неравенства
![]() на
на
![]() получим
получим
![]()
Линейный коэффициент
корреляции связан с коэффициентом
регрессии в виде следующей зависимости:![]() где
где
![]() —
коэффициент регрессии,
—
коэффициент регрессии,
![]() —
среднеквадратическое отклонение
соответствующего факторного признака.
—
среднеквадратическое отклонение
соответствующего факторного признака.
Для графического представления подобной связи можно использовать прямоугольную систему координат с осями, которые соответствуют обеим переменным. Каждая пара значений маркируется при помощи определенного символа. Такой график называется «диаграммой рассеяния».
Метод вычисления
коэффициента корреляции зависит от
вида шкалы, к которой относятся переменные.
Так, для измерения переменных с
интервальной и количественной шкалами
необходимо использовать коэффициент
корреляции Пирсона (корреляция моментов
произведений). Если по меньшей мере одна
из двух переменных имеет порядковую
шкалу, либо не является нормально
распределённой, необходимо использовать
ранговую корреляцию Спирмена или
![]() (тау)
Кендалла. В случае, когда одна из двух
переменных является дихотомической,
используется точечная двухрядная
корреляция, а если обе переменные
являются дихотомическими: четырёхполевая
корреляция. Расчёт коэффициента
корреляции между двумя недихотомическими
переменными не лишён смысла только
тогда, когда связь между ними линейна
(однонаправлена).
(тау)
Кендалла. В случае, когда одна из двух
переменных является дихотомической,
используется точечная двухрядная
корреляция, а если обе переменные
являются дихотомическими: четырёхполевая
корреляция. Расчёт коэффициента
корреляции между двумя недихотомическими
переменными не лишён смысла только
тогда, когда связь между ними линейна
(однонаправлена).
Корреляционная матрица случайного вектора (нашел 2 варианта, какой точней не знаю)
1 вариант
Корреляционная матрица — матрица коэффициентов корреляции нескольких случайных величин с ненулевыми дисперсиями
![]()
в которой элементы
![]() есть
коэффициенты корреляции соответствующих
случайных величин. Диагональные элементы
матрицы равны единице. Справедливо
соотношение
есть
коэффициенты корреляции соответствующих
случайных величин. Диагональные элементы
матрицы равны единице. Справедливо
соотношение
![]() ,
где
,
где
![]() —
диагональная матрица с элементами
—
диагональная матрица с элементами
![]() .
.
2 вариант
 -
корреляционная матрица
вектора Х.
-
корреляционная матрица
вектора Х.
На
главной диагонали КХ
- характеристики точности, квадраты
средних квадратических ошибок случайных
величин
![]() (оценки
дисперсий). Недиагональные элементы -
характеристики связи случайных величин
Xi,
Xj
- корреляционные моменты
(оценки
дисперсий). Недиагональные элементы -
характеристики связи случайных величин
Xi,
Xj
- корреляционные моменты
![]()
Вводят
 -
вектор математических ожиданий.
-
вектор математических ожиданий.
Тогда корреляционную матрицу КХ можно представить в виде:
![]()
где Х и МХ - вектора.
