24. Полигон и гистограмма.

Для наглядности строят различные графики статистического распределения и, в частности, полигон и гистограмму.

Полигоном частот называют ломаную, отрезки которой соединяют точки Для построения полигона частот на оси абсцисс откладывают варианты , на оси ординат - соответствующие им частоты . Точки соединяют отрезками прямых и получают полигон частот.

Полиногом относительный частот называют ломаную, отрезки которой соединяют точки . Для построения полигона относительных частот на оси абсцисс откладывают варианты , а на оси ординат—соответствующие им относительные ча­стоты . Точки соединяют отрезками прямых и получают полигон относительных частот.

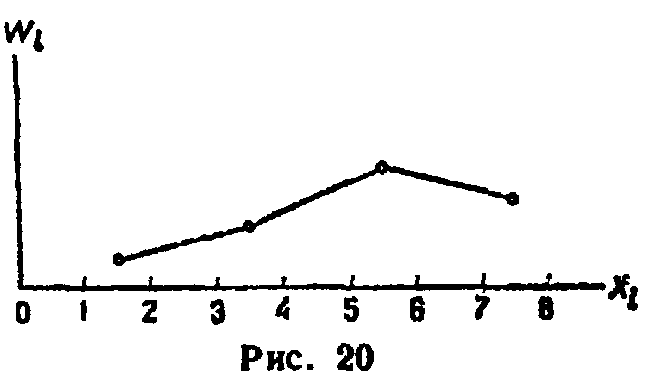
На рис. 20 изображен паолигон относительных ча­стот следующею распре­деления:

В случае непрерывного признака целесо­образно строить гистограмму, для чего интервал, в ко­тором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала —сумму частот вари­ант, попавших в интервал.

Гистограммой называют ступенчатую фигуру, состоя­щую из прямоугольни­ков, основаниями кото­рых служат частичные интервалы длиною h, а высоты равны отношению (плотность ча­стоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии .

Площадь частичного прямоугольника равна - сумме- частот вариант i-го интервала; следо­вательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

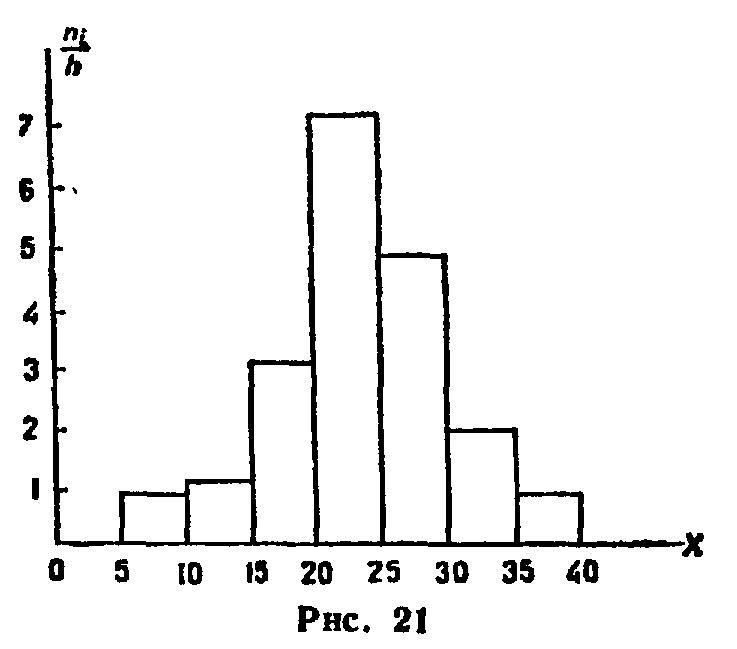
На рис. 21 изображена гистограмма частот распределения объема n = IOO, приведенного в табл. 6.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению (плотность относительной частоты).

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии . Площадь i-го частичного прямоугольника равна - относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

25. Генеральная и выборочная средние, их свойства. Оценка генеральной средней по выборочной.

Генеральная средняя

Пусть изучается дискретная генеральная совокуп­ность относительно количественного признака X.

Генеральной средней называют среднее арифметичес­кое значений признака генеральной совокупности.

Если все значения признака генераль­ной совокупности объема N различны, то

Если же значения признака имеют соответственно частоты , причем , то

т. е. генеральная средняя есть средняя взвешенная зна­чений признака с весами, равными соответствующим ча­стотам.

Выборочная средняя

Пусть для изучения генеральной совокупности относительно количественного признака X извлечена вы­борка объема n.

Выборочной средней называют среднее арифмети­ческое значение признака выборочной совокупности.

Если все значения признака выборки объема n различны, то

Если же значения признака имеют соот­ветственно частоты , причем , то

или

т. е. выборочная средняя есть средняя взвешенная зна­чений признака с весами, равными соответствующим ча­стотам.

Оценка генеральной средней по выборочной.

Пусть из генеральной совокупности (в резуль­тате независимых наблюдений над количественным при­знаком X) извлечена повторная выборка объема n со значениями признака . Не уменьшая общ­ности рассуждений, будем считать эти значения признака различными. Пусть генеральная средняя неизвестна и требуется оценить ее по данным выборки. В каче­стве оценки генеральной средней принимают выборочную среднюю

Убедимся, что — несмещенная оценка, т. е. покажем, что математическое ожидание этой оценки равно . Будем рассматривать как случайную величину как независимые, одинаково распределенные случайные величины . .Поскольку эти величины оди­наково распределены, то они имеют одинаковые числовые характеристики, в частности одинаковое математическое ожидание, которое обозначим через а. Так как матема­тическое ожидание среднего арифметического одинаково распределенных случайных величин равно математическому ожиданию каждой из, то

Приняв во внимание, что каждая из величин , имеет то же распределение, что и генеральная совокупность (которую мы также рассматриваем как слу­чайную величину), заключаем, что и числовые характе­ристики этих величин и генеральной совокупности оди­наковы. В частности, математическое ожидание а каждой из величин равно математическому ожиданию признака X генеральной совокупности, т. е.

Заменив в формуле (*) математическое ожидание а на , окончательно получим

Тем самым доказано, что выборочная средняя есть не­смещенная оценка генеральной средней.