13. Равномерный закон распределения
Определение: Непрерывная случайная величина Х имеет равномерный закон распределения на некотором интервале (а;b), которому принадлежат все возможные значения Х, если плотность распределения вероятностей f(x) постоянная на этом интервале и равна 0 вне его, т.е.
0
при х≤а,
f(х)=
при a<х<b,
0 при х≥b .
График функции f(x) изображен на рис. 1
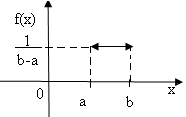
(рис.
1)
(рис.2)
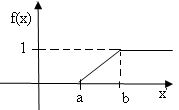
Функция распределения случайной величины Х, распределенной по равномерному закону, задается формулой:
0 при х≤а,
F(х)=
при a<х≤b,
0 при х>b.
Ее график изображен на рис. 2.
Числовые характеристики случайной величины равномерно распределенной на интервале (a;b), вычисляются по формулам:
M(Х)=
,
D(X)=
,
σ(Х)=
.
Задача№1. Случайная величина Х равномерно распределена на отрезке [3;7]. Найти:
а) плотность распределения вероятностей f(x) и построить ее график;
б) функцию распределения F(x) и построить ее график;
в) M(X),D(X), σ(Х).
Решение: Воспользовавшись формулами, рассмотренными выше, при а=3, b=7, находим:
0 при х<3,
а)
f(х)=
при 3≤х≤7,
0 при х>7
Построим ее график (р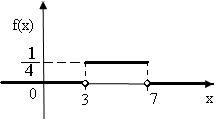ис.3):
рис.3
б) 0 при х≤3,
F(х)=
при 3<х≤7,
1 при х>7 .
Построим ее график (р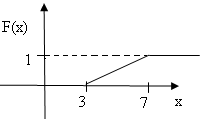ис.4):
рис.4
в)
M(X) =
=
=5,
D(X)
=
=
=
,
σ
(Х) =
=
=
.
Понятие многомерной (векторной) св и ее закон, функция и плотность распределения. Условные математические ожидания и дисперсии. Многомерные случайные величины
Многомерная
случайная величина
- это совокупность случайных величин
,
заданных на одном и том же вероятностном
пространстве
.
Закон распределения вероятностей многомерной случайной величины задаётся её функцией распределения
,
которая является
числовой функцией многих переменных и
(как вероятность) принимает значения
на отрезке
.
Функция распределения многомерной случайной величины обладает следующими свойствами.
для всех
:
;
(3.57)
не
убывает по каждому аргументу; (3.58)
непрерывна слева по каждому аргументу; (3.59)
;
(3.60)
.
(3.61)
В отличие от
одномерного случая, выполнение свойств
(3.57) - (3.61) для некоторой функции
не
гарантирует, что эта функция является
функцией распределения некоторой
многомерной случайной величины.
Многомерные случайные величины, так же, как и одномерные, могут быть дискретными (когда наборы возможных значений образуют конечное или счётное множество) или непрерывными (когда множество наборов возможных значений несчётно).
Всюду ниже в данном параграфе будут рассматриваться двумерные случайные величины.
Вероятность попадания двумерной случайной величины в полуоткрытый прямоугольник равна
(3.62)
.
Если дополнительно
к условиям (3.57) - (3.61) потребовать от
функции
неотрицательности
величины
для любых
таких,
что
,
то тогда эта функция обязательно будет
являться функцией распределения
некоторой двумерной случайной величины.
Двумерные дискретные случайные величины удобно задавать с помощью таблиц распределения
.
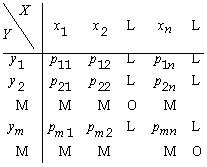(3.63)
В такой таблице
заголовки столбцов
соответствуют
всем возможным значениям первой
компоненты
,
а названия строк
-
всем возможным значениям второй
компоненты
.
При этом в клетку, находящуюся в
-й
строке и в
-м
столбце, записывается значение вероятности
.
Естественно,
.
(3.64)
Функция распределения двумерной дискретной случайной величины равна
.
(3.65)
Законы распределения каждой из компонент такой двумерной случайной величины (так называемые маргинальные законы распределения) восстанавливаются по таблице распределения (3.63) при помощи формул
.
(3.66)
Двумерная случайная величина называется абсолютно непрерывной, если её функция распределения может быть представлена в виде
,
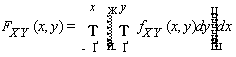(3.67)
при этом функция
называется
плотностью распределения двумерной
случайной величины
.
Плотность распределения абсолютно непрерывной двумерной случайной величины обладает следующими свойствами:
для всех
:
;
(3.68)
,
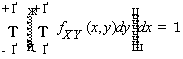(3.69)
причём любая функция, обладающая этими свойствами (3.68) - (3.69), является плотностью распределения некоторой абсолютно непрерывной двумерной случайной величины.
Если функция
распределения абсолютно непрерывной
двумерной случайной величины
имеет
смешанную частную производную
,
то плотность распределения
равна
этой частной производной:
.
(3.70)
Если абсолютно непрерывная двумерная случайная величина имеет плотность , то одномерные случайные величины и также являются абсолютно непрерывными, и их плотности можно рассчитать по формулам
.
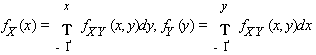(3.71)
Свойство (3.71)
справедливо только для двумерных
абсолютно непрерывных случайных
величин. В случае
это
свойство выглядит существенно иначе.
Условное математическое ожидание
Между случайными
величинами может существовать
функциональная зависимость. Например,
если
—
случайная величина и
,
то
—
тоже случайная величина, связанная с
функциональной
зависимостью. В то же время между
случайными величинами может существовать
зависимость другого рода, называемая
стохастической. В разделе, посвященном
условным распределениям уже обсуждалась
такая зависимость. Из рассмотренных
там примеров ясно видно, что информация
о значении одной случайной величины
(одной компоненты случайного вектора)
изменяет распределение другой случайной
величины (другой компоненты случайного
вектора), а это может, вообще говоря,
изменить и числовые характеристики
случайных величин.
Математическое ожидание, вычисленной по условному распределению, называется условным математическим ожиданием.
Для двумерного
дискретного случайного вектора
с
распределением
|
|
|
... |
|
|
|
|
... |
|
|
|
|
... |
|
... |
... |
... |
... |
... |
|
|
|
... |
|
условное
математическое ожидание случайной
величины
при
условии, что случайная величина
принимает
значение
,
вычисляется по формуле
.
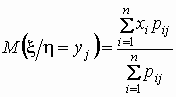Аналогично, условное
математическое ожидание случайной
величины
при
условии, что случайная величина
принимает
значение
,
равно
.
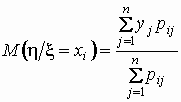