4. Независимость событий. Условные вероятности. Теоремы об умножениях вероятностей зависимых и независимых событий. Условная вероятность

Пример 18. Игральная кость подбрасывается один раз. Известно, что выпало более трёх очков. Какова вероятность того, что выпало чётное число очков?

Зная, что выпало более трёх очков, мы можем сузить множество всех возможных элементарных исходов до трёх одинаково вероятных исходов:  , из которых событию  благоприятствуют ровно два:  . Поэтому  .

Посмотрим на вопрос с точки зрения первоначального эксперимента. Пространство элементарных исходов при одном подбрасывании кубика состоит из шести точек:  . Слова «известно, что выпало более трёх очков» означают, что в эксперименте произошло событие  . Слова «какова при этом вероятность того, что выпало чётное число очков?» означают, что нас интересует, в какой доле случаев при осуществлении  происходит и  . Вероятность события  , вычисленную в предположении, что о результате эксперимента уже что-то известно (событие   произошло), мы будем обозначать через  .

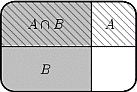
Мы хотим найти, какую часть составляют исходы, благоприятствующие   внутри   (т.е. одновременно   и  ), среди исходов, благоприятствующих  .

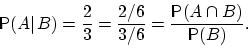
Мы пришли к выражению, которое можно считать определением условной вероятности.

Определение 18. Условной вероятностью события   при условии, что произошло событие  , называется число

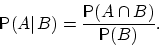
Условная вероятность определена только в случае, когда  .

Это определение бывает полезно использовать не для вычисления условной вероятности, а для последовательного вычисления вероятности нескольким событиям случиться одновременно, если известны соответствующие условные вероятности. А именно, справедливы следующие «теоремы умножения вероятностей».

Теорема 6. Если   и  , то

Теорема 7. Для любых событий   верно равенство:

если все участвующие в нём условные вероятности определены.

Независимость событий

С понятием условной вероятности тесно связано понятие независимости событий. Вообще, можно определить понятие независимости и безотносительно к условной вероятности. А именно, двасобытия называются независимыми, если вероятность их пересечения равна произведению их вероятностей:

Р(АВ)=Р(А)Р(В)

Из этого определения, однако, сразу следует, что условная вероятность А при условии В равна безусловной вероятности А:

и также, что условная вероятность В при условии А равна безусловной вероятности В:

Более того, любое из условий Р(А|В)=Р(А) или Р(В|А)=Р(В) влечет выполнение соотношения

Р(АВ)=Р(А)Р(В)

определяющего независимость.

События  А , В   Е называются независимыми, если  Р ( А   В ) = Р ( А ) · Р ( В ) .

В противном случае события  А и В называются зависимыми.

Примеры.

1.       Рассмотрим два события: А - попадание частицы в левую половину фотопластинки, В - попадание частицы в нижнюю четверть фотопластинки. События А и В имеют вероятности 1/2 и 1/4. Событие АВ,соответствующее попаданию частицы в пересечение А и В, т.е. в левый нижний угол фотопластинки, имеет вероятность 1/8. Поскольку 1/8=1/2*1/4, т. е. Р(АВ)=Р(А)Р(В), то события А и В независимы.

2.       Зависимы ли события «наличие доминантного признака» {АА, Аа, аА} и гомозиготность {АА, аа}? Вероятность первого события равна 3/4, вероятность второго - 1/2. Вероятность их пересечения равна 1/4. Поскольку 1/4¹3/4*1/2, то события не являются независимыми.

К этому же выводу можно прийти иначе. Мы видели, что вероятность гомозиготности при наличии доминантного аллеля равна 1/3. Вообще же вероятность гомозиготного потомка равна 1/2. Таким образом, условная вероятность не равна безусловной и, следовательно, события зависимы.

3.       Рассмотрим случайное испытание, состоящее из двух последовательных бросаний монеты. Результатом этого события будут четыре равновероятных элементарных события: герб - герб, герб - решка, решка - герб, решка - решка (или ГГ, ГР, РГ, РР). Зависимы ли события «выпадение герба в первом бросании» А={ГГ, ГР} и «выпадение герба во втором бросании» В={ГГ, РГ}? Имеем Р(A)=1/2,Р(B)=1/2, Р(AB)=Р(ГГ)=1/4. Поскольку Р(АВ)=Р(А)Р(В), то события независимы.