- •Содержание
- •Введение в теорию принятия решений
- •Тема 1. Теория принятия решений – модель исследования операций
- •1.1. Основные понятия исследования операций
- •1.2. Операционный подход к решению задач
- •1.3. Классификация моделей в исследовании операций
- •Классы операционных задач
- •1. Задачи управления запасами
- •2. Задачи распределения
- •3. Задачи массового обслуживания
- •4. Задачи выбора маршрута
- •5. Задачи замены оборудования
- •6. Задачи упорядочения
- •7. Задачи сетевого планирования и управления
- •8. Состязательные задачи
- •9. Задачи поиска
- •Тема 2. Линейное программирование
- •2.1. Задача линейного программирования
- •2.2. Графический метод решения злп
- •Алгоритм решения задач лп графическим методом
- •2.3. Решение злп симплексным методом
- •1 Симплексная таблица
- •2 Симплексная таблица
- •3 Симплексная таблица
- •4 Симплексная таблица
- •1 Симплексная таблица
- •2 Симплексная таблица
- •3 Симплексная таблица
- •2.4. Теория двойственности в линейном программировании
- •Пример №2.7.
- •2.5. Классическая транспортная задача (ктз)
- •2.6. Общая распределительная задача линейного программирования
Тема 2. Линейное программирование
2.1. Задача линейного программирования
Многие практические задачи сводятся к случаю, когда необходимо найти либо максимум или минимум функции f(x1, x2,…, xn):
f(x1, x2,…, xn)→max(min), (2.1)
и на переменные x1, x2, …, xn наложены различные ограничения в виде неравенств или равенств:
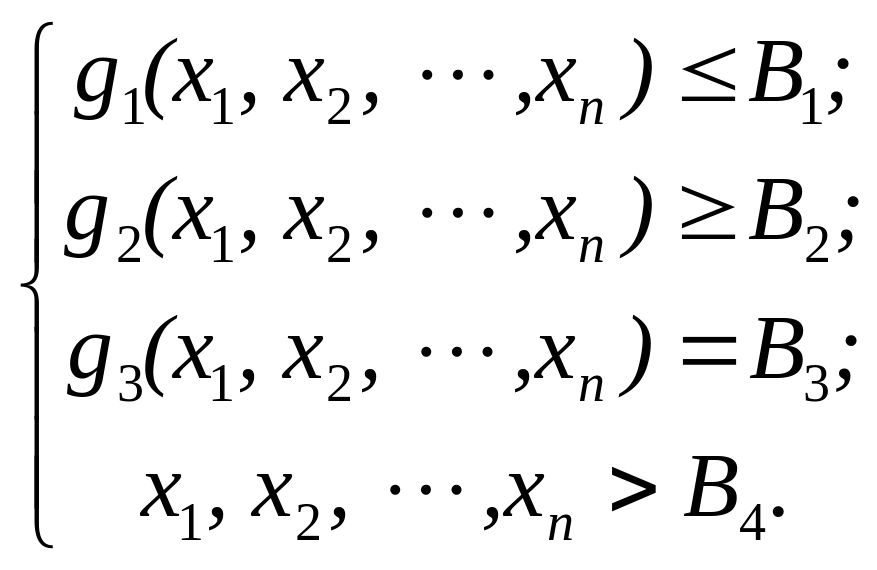
![]()
Функция (2.1) называется функцией цели (целевой функцией, линейной функцией, линейной формой).
Соотношения (2.2) – (2.5) представляют собой запись условий ограничений (неравенств ограничений, система ограничений) функции (2.1).
Программирование – нахождение экстремума (max или min) функции (2.1) при заданных ограничениях (2.2) – (2.5), т.е. другими словами, найти оптимальное решение функции f(x1, x2, …, xn) при наложенных ограничениях.
Линейное программирование (задачи линейного программирования) – это нахождение оптимального решения (оптимального плана) при условии, что функция цели f(x1, x2, …, xn) линейна, все условия ограничения линейны и x1, x2, …, xn ≥ 0.
Пусть имеется n переменных x1, x2, …, xn. Необходимо найти такие значения этих переменных, чтобы достигался max или min функции цели (линейной):
F=c1x1+c2x2+…+cnxn→max(min), (2.6)
при соответствующей системе ограничений:
 (2.7)
(2.7)
Для конкретной практической задачи система ограничений может содержать любой из знаков неравенства. Но сами переменные x1, x2, …, xn всегда должны быть больше либо равны нулю.
Необходимо найти решение системы ограничений X=(x1, x2, …, xn), при котором функция цели (2.6) будет принимать экстремальное значение (max или min). При этом данное решение должно удовлетворять системе ограничений (2.7). Нахождение такого решения и составляет задачу линейного программирования (ЗЛП).
Задачу линейного программирования можно записать и в более краткой форме:
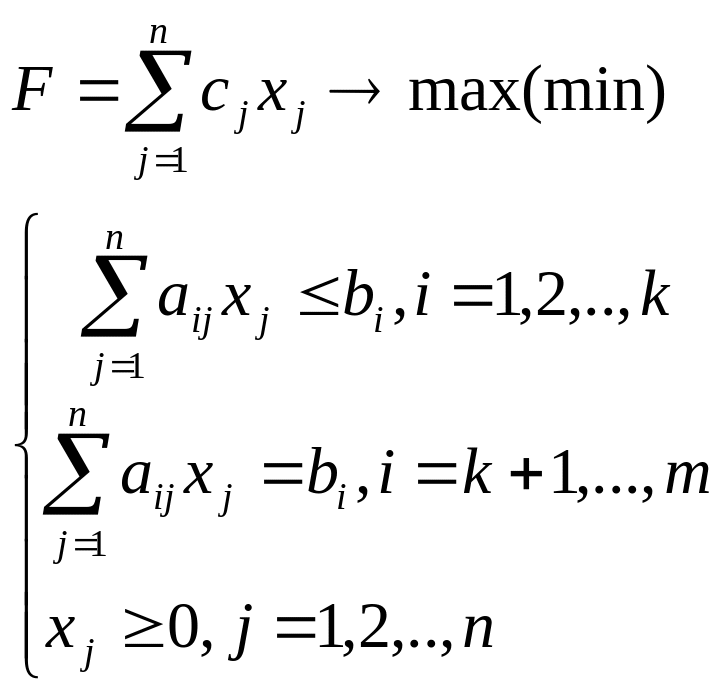 (2.8)
(2.8)
Общей задачей линейного программирования называется задача, записанная в форме (2.8) (т.е. в системе ограничений присутствуют как неравенства, так и равенства)
Стандартной задачей линейного программирования называется задача, система ограничений в которой состоит только из одних неравенств и все неизвестные больше либо равны нулю:
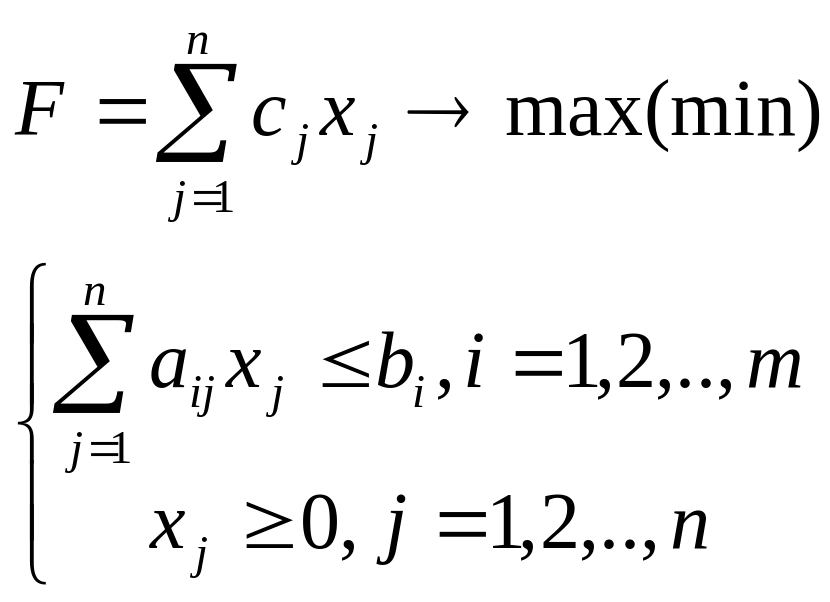 (2.9)
(2.9)
Канонической задачей линейного программирования называется задача, которая состоит в определении максимального значения функции цели, и система ограничений в которой состоит только из одних уравнений (все неизвестные переменные должны быть больше либо равны нулю):
 (2.10)
(2.10)
Линейная производственная задача, или задача о рациональном использовании производственных мощностей (имеющихся ресурсов), является одной из первых задач, для решения которой применяют методы линейного программирования. В общем виде математическая модель задачи может быть сформулирована следующим образом.
Предприятие
выпускает
![]() видов изделий,
имея
видов изделий,
имея
![]() групп оборудования. Известны нормы
времени на обработку каждого изделия
на каждой группе оборудования (например,
в минутах или часах) и фонд времени
работы каждой группы оборудования.
Требуется составить план производства,
при котором предприятие получит
наибольшую прибыль.
групп оборудования. Известны нормы
времени на обработку каждого изделия
на каждой группе оборудования (например,
в минутах или часах) и фонд времени
работы каждой группы оборудования.
Требуется составить план производства,
при котором предприятие получит
наибольшую прибыль.
Пусть:
i номер группы оборудования (i=1,2,…,m);
j номер вида изделия (j=1,2,…,n) ;
aij норма времени на обработку единицы j-ого изделия на i-й группе оборудования;
bi фонд времени работы i-й группы оборудования;
cj прибыль на одно изделие j-ого вида;
xj планируемое количество единиц j-ого изделия;
![]() искомый план
производства.
искомый план
производства.
Какова бы ни была производственная
программа
![]() ,
ее компоненты должны удовлетворять
условию: суммарное время обработки всех
изделий на данной группе оборудования
не должно превышать фонда времени работы
этой группы оборудования.
,
ее компоненты должны удовлетворять
условию: суммарное время обработки всех
изделий на данной группе оборудования
не должно превышать фонда времени работы
этой группы оборудования.
На обработку x1 единиц первого изделия на i-й группе оборудования будет затрачено ai1x1 единиц времени; на обработку x2 единиц второго изделия на той же группе оборудования будет затрачено ai2x2 единиц времени и т. д.
Необходимое время на обработку всех
![]() изделий
на i-й группе оборудования
будет равно сумме
изделий
на i-й группе оборудования
будет равно сумме
![]() .
.
Эта
сумма не может превышать фонд времени
работы i-й
группы оборудования, т. е. должна быть
меньше либо равна
![]() .
Выписывая такие
условия для всех m
групп оборудования, формирется система:
.
Выписывая такие
условия для всех m
групп оборудования, формирется система:
 (2.11)
(2.11)
Т.к. компонентами плана, по сути, является количество изделий и, следовательно, не могут быть выражены отрицательными числами, то естественным образом добавляются условия
![]() .
.
При плане производства ( ) прибыль предприятия будет равна
![]() .
(2.12)
.
(2.12)
Необходимо составить производственную программу так, чтобы функция F приняла наибольшее возможное значение при выполнении всех условий.
Система линейных неравенств (2.11) и линейная форма (2.12) образуют математическую модель задачи о рациональном использовании производственных мощностей. Среди всех решений системы линейных неравенств (2.11), удовлетворяющих условию неотрицательности переменных, необходимо найти такое решение, при котором линейная форма (2.12) принимает наибольшее возможное значение. Это — задача линейного программирования.
Исходные параметры задачи могут быть представлены в виде матрицы А удельных затрат ресурсов, вектора В объемов ресурсов и вектора С удельной прибыли:
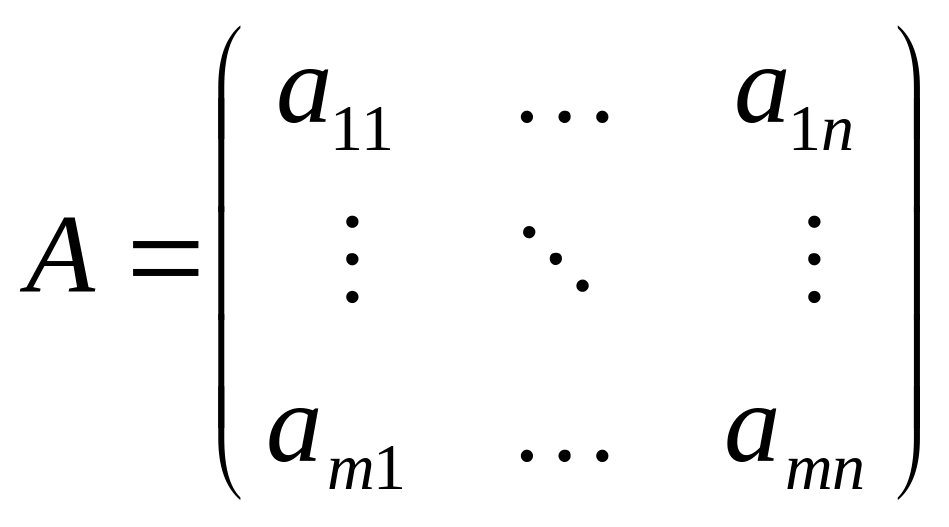

![]()
Классическая задача линейного программирования задача о распределении производственной программы.
Производственное объединение получило заказ на изготовление n видов изделий в количествах d1, d2, …, dn соответственно. Объединению подчинены m предприятий, на каждом из которых может быть выполнен заказ на любое изделие.
Пусть
bi действительный фонд времени работы i-го предприятия;
aij и cij соответственно норма расхода времени и себестоимость изготовления единицы j-го изделия на i-м предприятии;
xij число изделий j-го вида, которое поручается изготовить i-му предприятию.
Задача состоит в том, чтобы найти распределение заказов между предприятиями, которое минимизирует суммарную себестоимость изготовления всех изделий
![]()
при условии, что будут соблюдены ограничения по фонду времени работы каждого предприятия
![]() ,
где
,
где
![]() ,
,
и будет изготовлено необходимое количество изделий каждого вида
![]() ,
,
![]() .
.
причем по смыслу задачи
![]() ,
где
,
.
,
где
,
.
Задача о диете. Необходимые в дневном рационе питания m видов питательных веществ содержатся в n видах продуктов.
Пусть
aij количество единиц i-го питательного вещества в единице j-го продукта;
bi необходимое количество единиц i-го питательного вещества в дневном рационе;
cj стоимость единицы j-го продукта.
Задача состоит в том, чтобы найти план покупок , минимизирующий суммарные затраты
![]()
при условии, что каждое питательное вещество будет содержаться в купленных продуктах в количестве не менее требуемого
![]() ,
где
,
,
где
,
причем по смыслу задачи
![]() ,
где
.
,
где
.
В задаче о загрузке требуется загрузить корабль различными типами грузов так, чтобы их суммарная ценность была наибольшей.
Пусть
j номер типа груза;
n число типов грузов;
a1j, a2j, cj масса, объем и стоимость единицы j-го груза;
b1, b2 грузоподъемность и вместимость грузового отсека корабля;
xj количество единиц j-го типа груза, который мы хотели бы погрузить.
Задача состоит в том, чтобы найти набор , максимизирующий суммарную ценность
![]()
при ограничениях по грузоподъемности и вместимости
,
где
![]() ,
,
где , xj – целое, .
Пример №2.1.
Составить математическую модель задачи.
Имеется два вида корма «№1» и «№2», содержащие питательные вещества: белки, жиры, углеводы. Содержание числа единиц питательных веществ в 1 кг каждого вида корма и необходимый минимум питательных веществ, а также их стоимость представлены в таблице 2.1.
Таблица 2.1.
Вид питательного вещества (витамина) |
Число единиц питательных веществ в 1 кг |
Необходимый минимум питательных веществ |
|
№1 |
№2 |
||
Белки |
3 |
1 |
9 |
Жиры |
1 |
2 |
8 |
Углеводы |
1 |
6 |
12 |
Стоимость 1 кг корма (руб) |
4 |
6 |
|
Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательных веществ было бы не менее установленного предела.
Решение.
Пусть x1 и x2 – количество кормов «№1» и «№2».
Тогда условия – ограничения для каждого вида питательного вещества составляются следующим образом: т.к. необходимо, чтобы содержание питательного вещества было не ниже установленного предела, то рацион должен включать питательных веществ либо больше установленного предела, либо строго этот предел.
Поэтому:
условие - ограничение для белков имеет вид:
![]() ,
,
условие – ограничение для жиров:
![]() ,
,
условие – ограничение для углеводов:
![]() .
.
Кроме того, переменные x1, x2 должны быть больше или равны нулю:
![]() .
.
Общая стоимость рациона составит:
![]() (руб).
(руб).
Т.к. общая стоимость дневного рациона должна быть минимальна, то необходимо найти минимум функции цели .
Ответ.
Математическая модель задачи имеет вид:
![]()
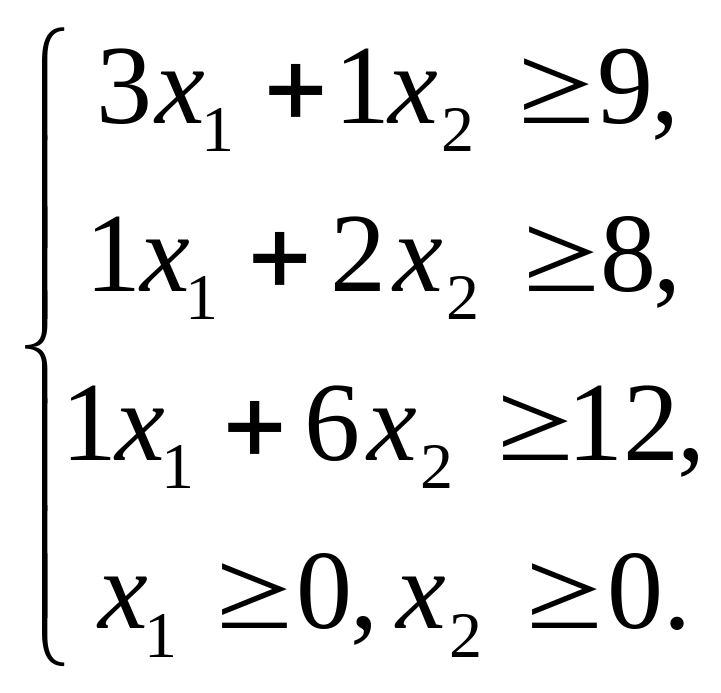
После расчета данной математической модели (ее решения) определяются значения x1, x2, удовлетворяющие системе ограничений и доставляющие минимум функции цели, т.е. рассчитывается состав минимальной потребительской корзины.
Пример №2.2.
Фабрика производит два вида красок: первый – для наружных, а второй – для внутренних работ. Для производства красок используются два ингредиента: А и В. Максимально возможные суточные запасы этих ингредиентов составляют 6 т и 8 т соответственно. Известны расходы А и В на 1 т соответствующих красок (табл. 2.2.). Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1-го вида более, чем на 1 т. Кроме того, установлено, что спрос на краску 2-го вида никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 тыс. руб. для краски 1-го вида и 2 тыс. руб. для краски 2-го вида.
Таблица 2.2.
Ингредиенты
|
Расход ингредиентов, т ингр./т краски |
Запас, т ингр./сутки
|
|
Краска 1-го вида |
Краска 2-го вида |
||
А |
1 |
2 |
6 |
В |
2 |
1 |
8 |
Необходимо построить математическую модель, позволяющую установить, какое количество краски каждого вида надо производить, чтобы доход от реализации продукции был максимальным.
Решение.
Запись условий – ограничений:
для ингредиента А в условиях запаса:
![]() (т
ингр.А/сутки),
(т
ингр.А/сутки),
для ингредиента В в условиях запаса:
![]() (т
ингр.В/сутки),
(т
ингр.В/сутки),
суточный спрос обоих ингредиентов:
![]() (т
краски/сутки),
(т
краски/сутки),
суточный спрос ингредиента В:
![]() (т
краски/сутки).
(т
краски/сутки).
Переменные x1, x2 должны быть больше или равны нулю:
.
Формирование функции цели:
доход от реализации продукции составит:
![]() (руб.
/сутки).
(руб.
/сутки).
Ответ.
Математическая модель задачи имеет вид:
![]()